ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
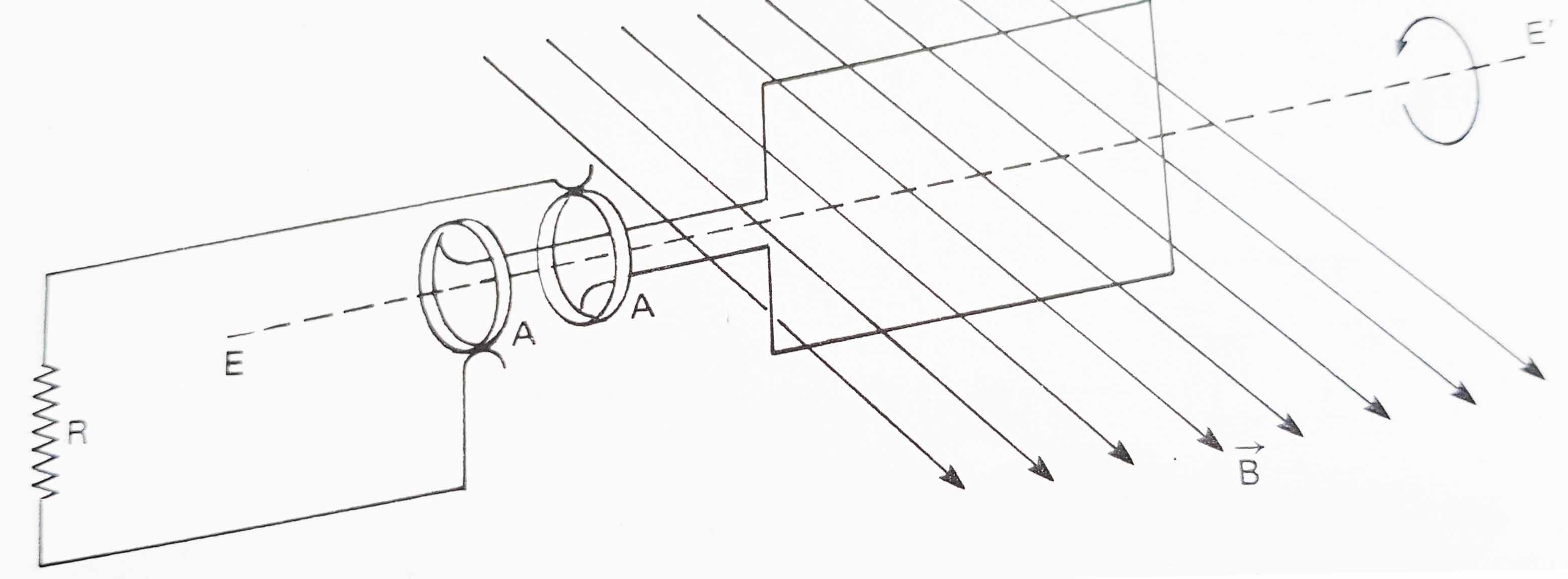
1*.Cuando se gira una
espira como la de la figura en el campo magnético de un imán, éste induce en
ella una corriente inducida, que recogida por unos anillos colectores AA pasa a
través de unos contactos generalmente de grafito, denominados escobillas a un
circuito externo. Esta corriente se denomina alterna y este nombre se debe a
que:
a) Su intensidad cambia
de sentido alternativamente cada giro de 180 grados)
b) Su fuerza
electromotriz varia sinusoidalmente con el tiempo
c) Porque se alternan los
bornes positivos y negativos en los anillos colectores
d)Porque al dar una
vuelta entera su intensidad y su fuerza electromotriz pasan de valores máximos a mínimos y viceversa

11. Si
se hace girar un conjunto de 10 espiras rectangulares de 10 por 5 cm de lado,
sobre su eje, con una frecuencia de 100 vueltas por segundo, dentro de un campo
magnético de 10Tesla, se podrá asegurar que la fuerza electromotriz generada a
los 3 segundos de comenzar a girar será:
a) 314V b)
31,4V c) 3,14V d) 0,314V
Si la resistencia óhmica
externa es de 10 ohmios, la intensidad de la corriente será de:
a) 3,14A b) 31,4A c) 0,314A d) 0A
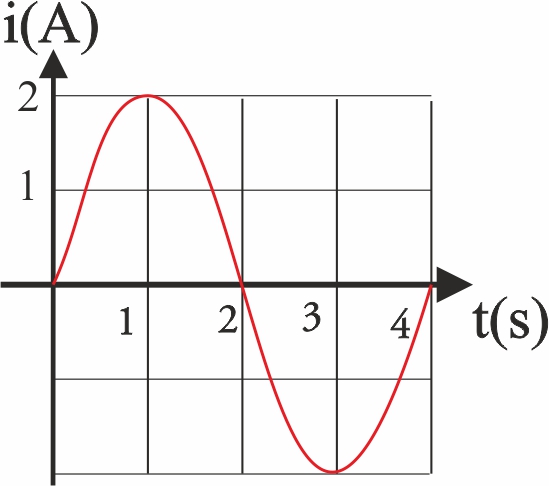
10. 20 espiras cuadradas
de 4cm. de lado y resistencia 10 ohmios, giran con una determinada velocidad en
un campo magnético constante, dispuesto perpendicularmente a ellas. Si la
intensidad de la corriente inducida varía con el tiempo tal como indica la gráfica,
se podrá decir que inicialmente la espiras formaban un ángulo con dicho campo
de:
a) 0º b) 90º c)
180º d) 270º
La velocidad angular con
la que giran será en rad/s de:
a)1 b)0,5π c)0,5 d)π
Si la fem máxima es de 20V, la intensidad del campo magnético será en teslas de:
a)104 b)102 c)2. 104 d)0,5
104
2. Se sabe que el flujo
magnético que atraviesa una espira rectangular, viene dado por el producto
escalar del vector intensidad de campo magnético B, y su vector superficie S (
vector perpendicular a ella, dirigido hacia afuera, y con su valor modular), y
por lo tanto dependerá del coseno del ángulo que forman ambos vectores Por ello
al girar ésta y variar el ángulo, se producirá una fuerza electromotriz
inducida, cuyo valor máximo se producirá, cuando dicho ángulo valga:
a) 90º b) 180º c) 0º d)
270º
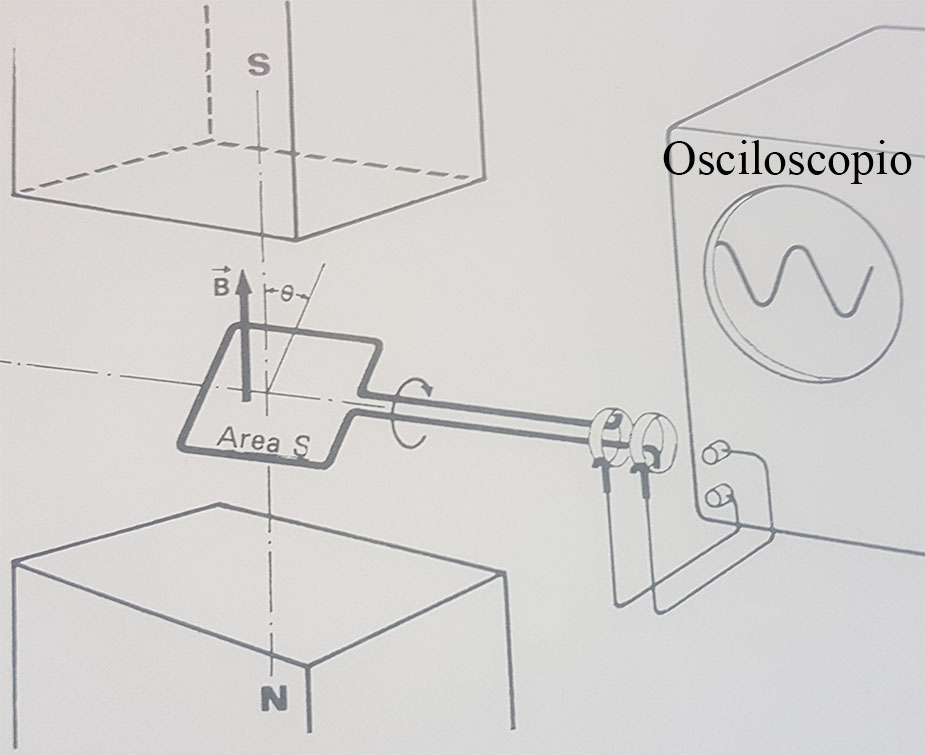
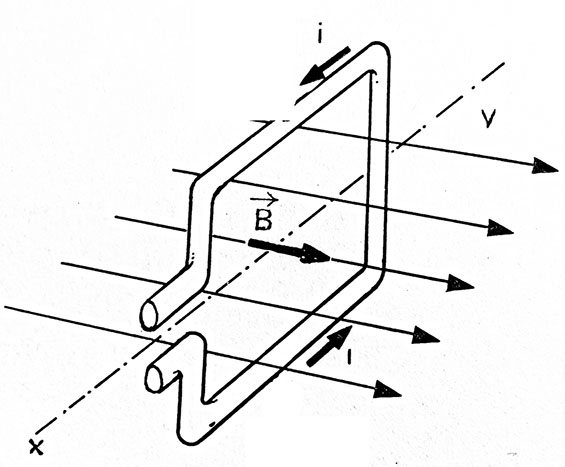
3.Si en un determinado instante la espira dada en el
test CA1, toma la disposición del dibujo, se podrá decir que:
a)El vector superficie tiene el mismo
sentido que la intensidad del campo magnético
b) El flujo magnético que la baña es
máximo
c)La fem que se
origina es mínima
d)La intensidad de la corriente inducida es 0
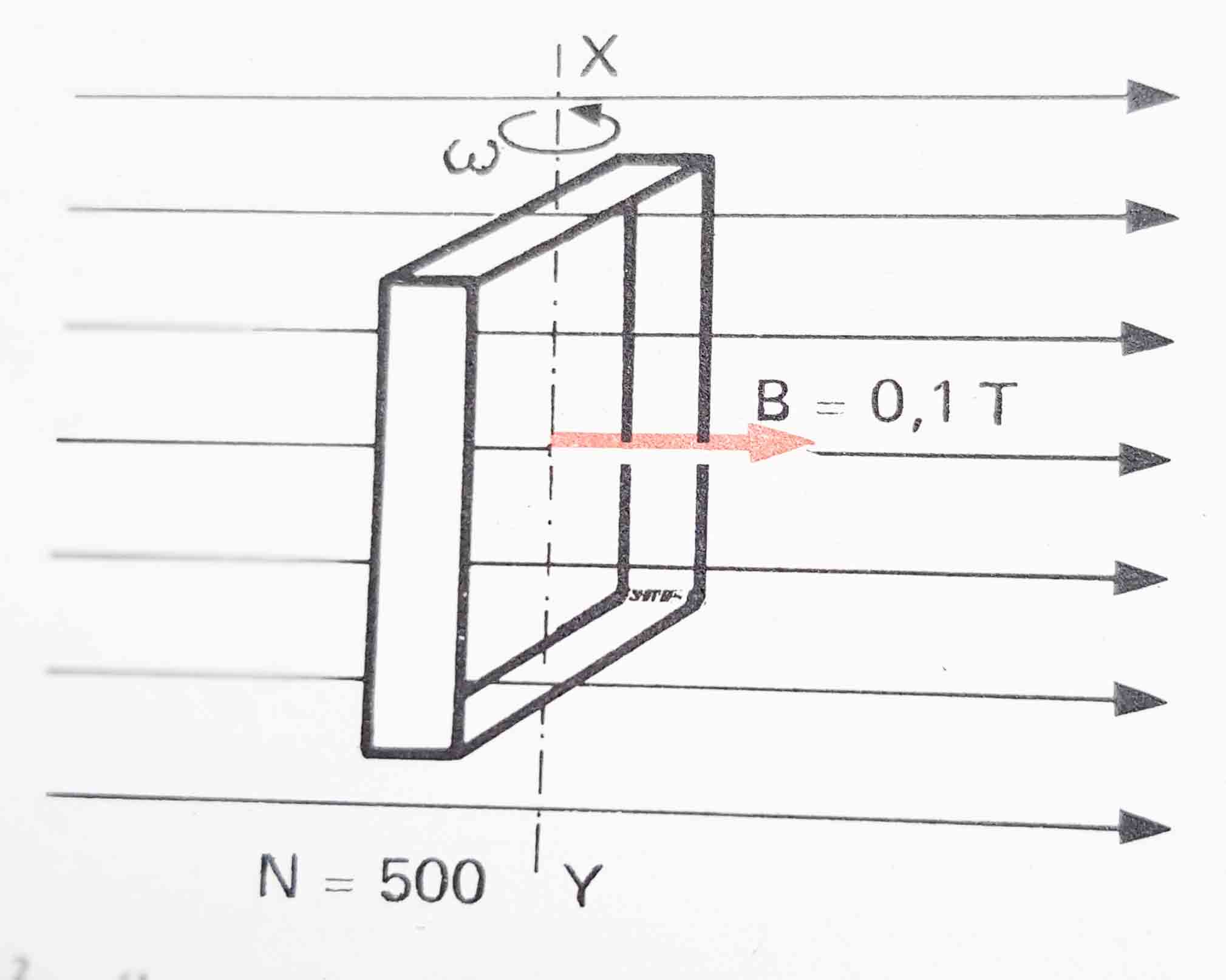
9. Una espira cuadrada de
0,1m de lado, gira del eje XY, en un campo magnético de 1T.Para que la fem máxima inducida en esta bobina sea de 10V, la velocidad con la que deberá
girar será en rad/s de:
a)100 b)1000 c)1000π d)100π
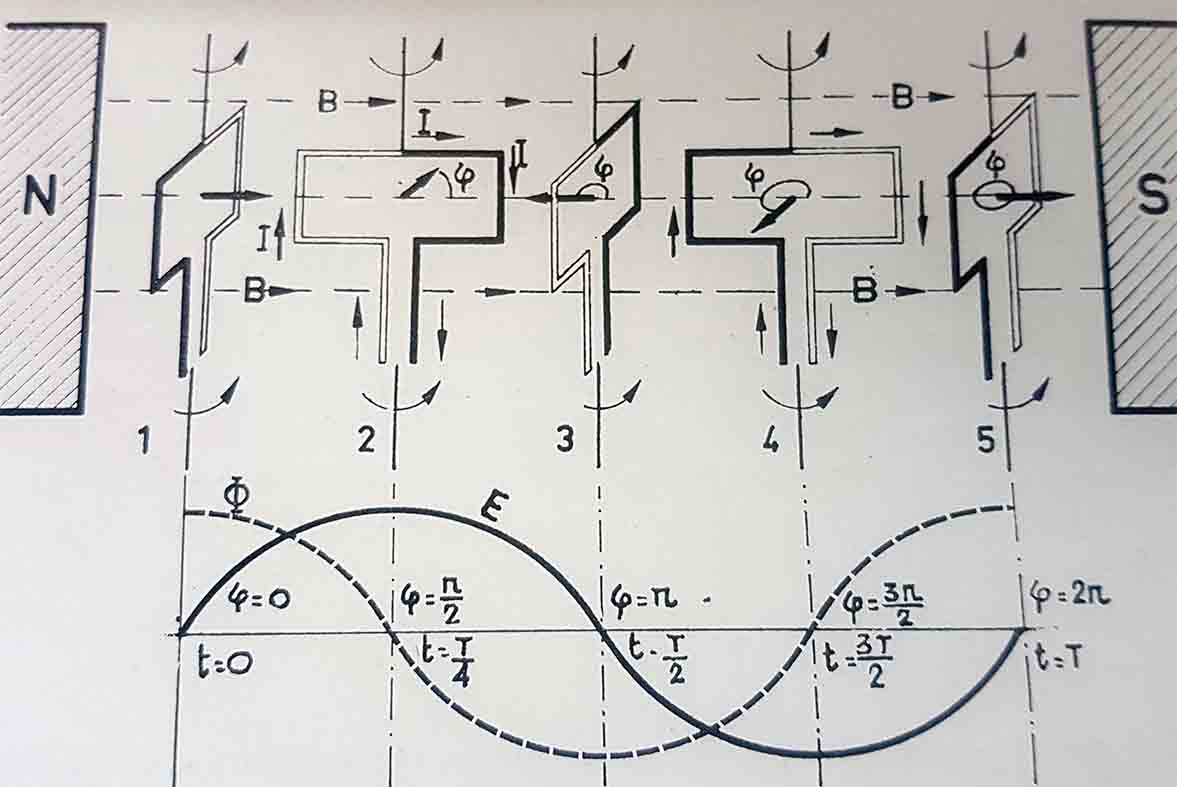
4*. Se dan las gráficas de la variación del del flujo
magnético y a fem inducida E, debida a dicha
variación correspondiente al movimiento giratorio de una espira en un campo
magnético. Ambas no coinciden en sus variaciones sinusoidales porque:
a) El flujo magnético depende del seno de
φ, mientras que la fem E depende del coseno de
φ
b) El flujo magnético depende del coseno
de φ, mientras que la fem E depende del seno de
φ
c) La definición del fem inducida
d) No coinciden en los tiempos
5*. Cuando una espira gira con una velocidad angular
ω constante, dado que ,q=ωt y
ω= 2π f, siendo f la frecuencia de su movimiento que a su vez es 1/T,
siendo T el periodo de este movimiento periódico, las expresiones del flujo y
fuerza electromotriz inducida cambiarán a :
a)E=B.S senωt=B.S.sen(2πf)=B.S. sen (2πt/T)
b) F = B.S.cosωt=B.S.cos(2πf)=B.S.
cos (2πt/T)
y teniendo en cuenta los valores serán
máximos cuando el sen=1, y cos =0, en estos casos
c) E=EM senωt=
EM sen(2πf)= EM sen (2πt/T)
d) F = FM.cosωt=FM cos(2πf)= FM cos (2πt/T)
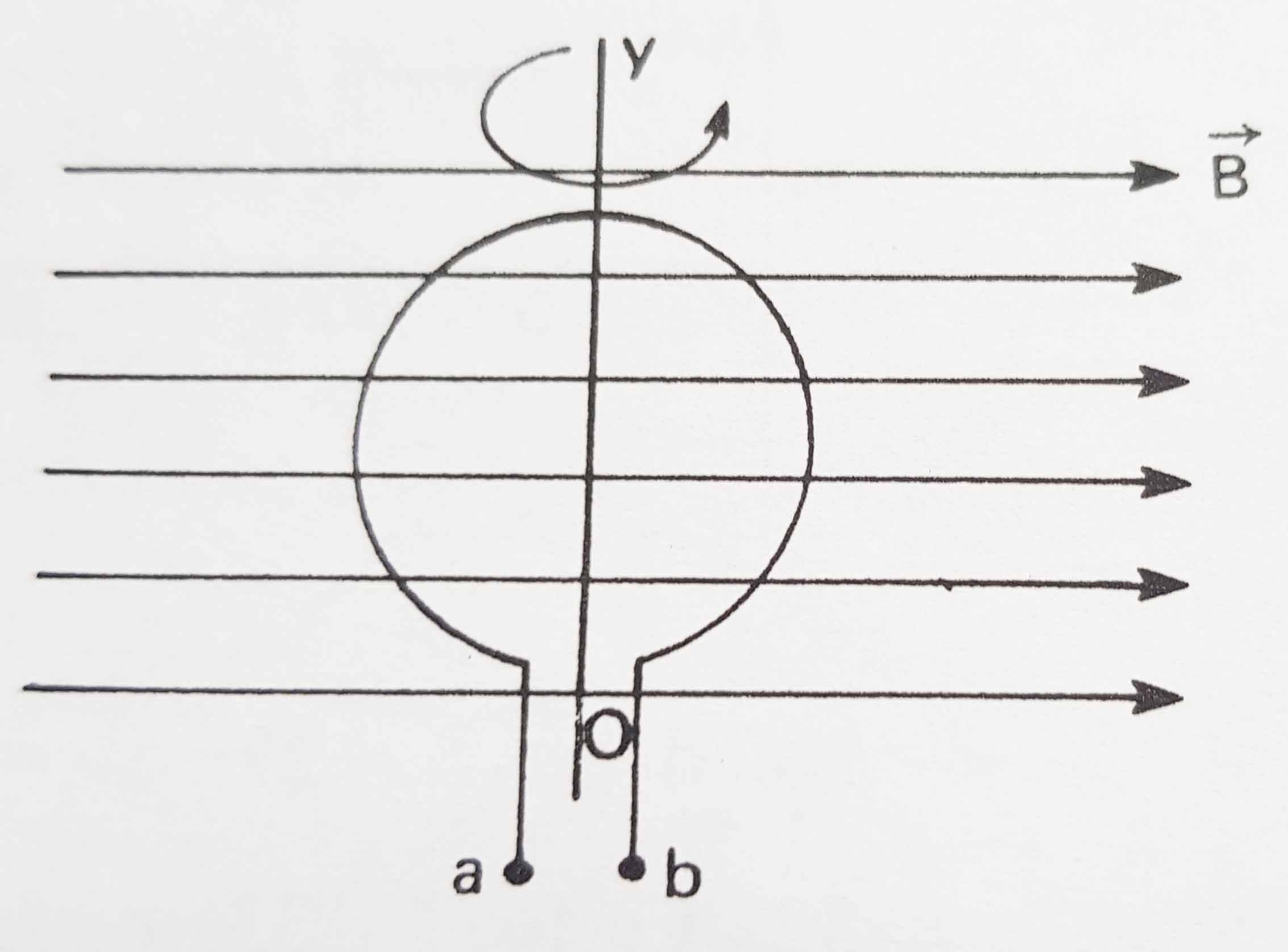
8.La espira circular dada
de radio 10cm, gira del eje OY, a 100vueltas por segundo, en un campo magnético
de 1T.Teniendo en cuenta que la resistencia óhmicas de la espira es de 10 ohmios. La intensidad de la
corriente que deberá circular por ella para que la fem sea máxima deberá ser de:
a) 0,2π2A b) π2A c) 2π2A d) 0,2πA
CORRIENTE ALTERNA 1
7. Una bobina formada por
500 espiras cuadradas de 6cm2 de superficie, girar en torno al eje XY, en un campo magnético de 0,1T. Si la bobina gira a 60 revoluciones por
segundo, se podrá asegurar que la fuerza electromotriz máxima generada será en
voltios de:
a) 0,6π b) 1,8π c) 3,6π d) -3,6π

ALMACÉN
Dinámica general I (continuación)
Aspectos energéticos(continuación)
Dinámica de las masas enlazadas
Dinámica de los sistemas no inerciales
Dinámica de los sistemas no inerciales(continuación)
Dinámica del movimiento circular
Determinación del centro de masas
Determinación del centro de masas(continuación)
Conservación de la cantidad de movimiento I
Conservación de la cantidad de movimiento(continuación)
Conservación de la cantidad de movimiento(masa variable)
Sistema de referencia del centro de masas I
Sistema de referencia del centro de masas II
Sólido rígido II(Fuerzas y momentos)
Sólido rígido II(Fuerzas y momentos, continuación)
Sólido rígido III(Fuerzas y momentos, final)
Sólido rígido IV(Energía y trabajo)
Sólido rígido V(Energía y trabajo, continuación)
Sólido rígido VI (Conservación del momento angular)
Sólido rígido VII(Conservación del momento angular, continuación)
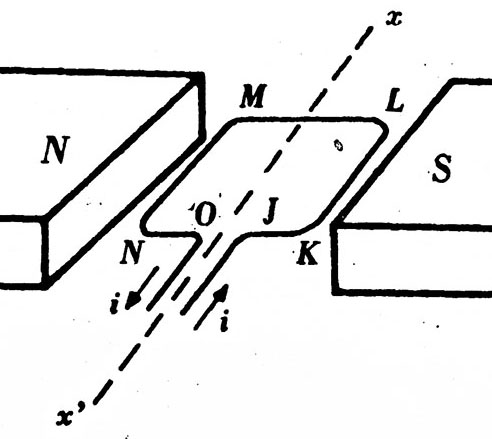
6.Por la espira cuadrada
KLMN, de 10cm de lado, circula una corriente de 2A, en el sentido indicado. La
espira es capaz de girar del eje xx´,y el campo
magnético a la que está sometida, vale 1T. Podrás asegurar que:
a) Gira hacia la derecha b) Gira hacia la izquierda c)No puede girar
Y el módulo del momento
de las fuerzas que la harían girar vale:
a)0,02mN b)-0,02mN c)0,2mN d)-0,2mN