a) A
b) B c) C
d) D
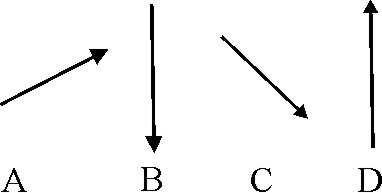
1.2.33.* Sabiendo que, para determinar el
sentido y dirección de la aceleración de un movimiento, se la descompone en
sus componentes intrínsecas, la aceleración tangencial y la aceleración normal,
que vienen indicadas en los puntos P1 y P2 de la figura,
se podría decir de ellas que:
a) LA
ACELERACIÓN TANGENCIAL ES PERPENDICULAR A LA VELOCIDAD
b) LA
ACELERACIÓN NORMAL ES PERPENDICULAR A LA VELOCIDAD
c) LA
ACELERACIÓN CENTRÍPETA ES PERPENDICULAR A LA TANGENTE A LA TRAYECTORIA EN
CADA INSTANTE Y ESTA DIRIGIDA HACIA EL CENTRO
d) LA
ACELERACIÓN TANGENCIAL SURGE COMO CONSECUENCIA DE LA VARIACIÓN DEL MÓDULO
DE LA VELOCIDAD
e) LA
ACELERACIÓN NORMAL ES NULA SI LA TRAYECTORIA ES RECTILÍNEA
f) EL
MÓDULO DE LA ACELERACIÓN TANGENCIAL ES IGUAL AL VALOR ABSOLUTO DE LA ACELERACIÓN
ESCALAR INSTANTÁNEA
g) EL
MÓDULO DE LA ACELERACIÓN NORMAL ES 0 EN EL MOVIMIENTO CIRCULAR UNIFORME
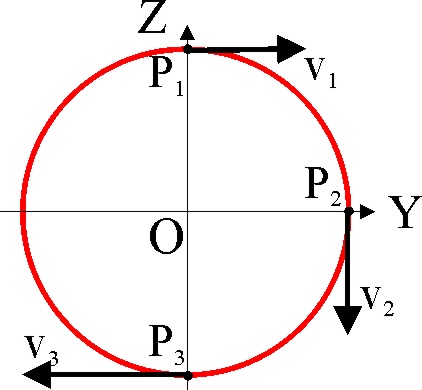
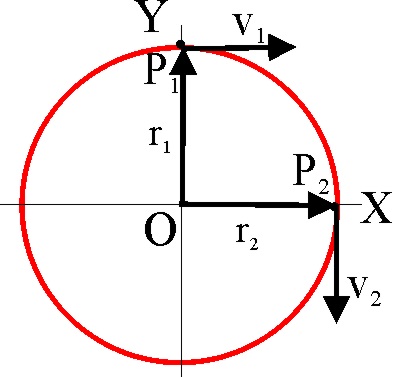
1.2.34.* Supuesto un punto móvil que recorre
una trayectoria circular en el plano YZ, con centro en O, en los instantes
t1, t2 y t3, se encuentra respectivamente
en P1, P2 y P3, siendo las velocidades las
indicadas en el dibujo y manteniendo o variando uniformemente su magnitud
en los intervalo dados, se podrá decir entonces que:
a) ENTRE
P1 Y P2, a=an,SI EL MODULO DE LA VELOCIDAD SE MANTIENE TAL
COMO SE INDICA EN EL DIBUJO
b) ENTRE
P2 Y P3, an=0 Y
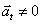
c) TIENE
PERMANENTEMENTE a DIRIGIDA HACIA O
d) SÓLO
TIENE a DIRIGIDA HACIA O ENTRE P1 Y P2
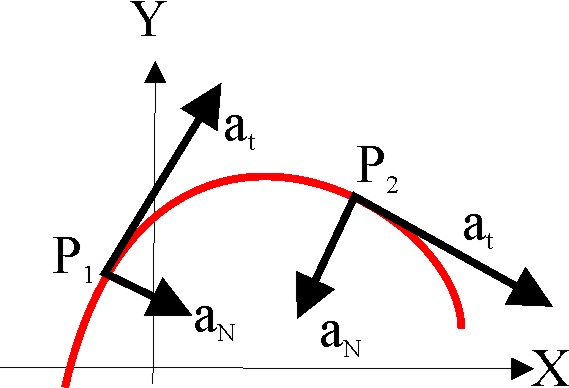
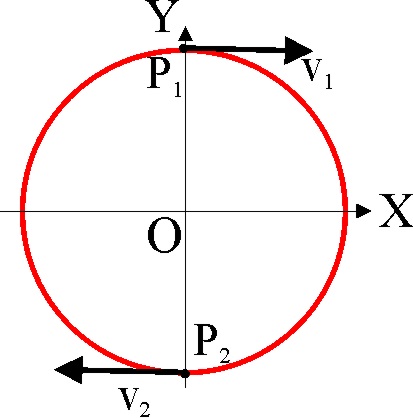
1.2.38.* En la gráfica de la figura, se
observa que en el instante t1, un punto móvil se encuentra en P1,
y en t2, en P2, indicándose en cada instante las aceleraciones
tangenciales del movimiento. Si se estudia con detenimiento la figura, se
podrá decir que:
a) EL MOVIMIENTO ES VARIADO
b) LA ACELERACIÓN TANGENCIAL ES IGUAL A
a
c) LA ACELERACIÓN CENTRÍPETA ES 0
d) EL MÓDULO DEL VECTOR VELOCIDAD SE MANTIENE
CONSTANTE
1.2.39. Relacione las condiciones vectoriales
de la columna izquierda, con el movimiento indicado a la derecha, uniéndolos
con una línea:
a) at=0
1) UNIFORME
b) an=0
2) RECTILÍNEO
c) an=0, at=0 3) RECTILÍNEO UNIFORME
d)
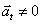 ,
,
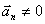 4) CURVILÍNEO
VARIADO
4) CURVILÍNEO
VARIADO
e) at=0,
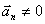 5)
RECTILÍNEO VARIADO
5)
RECTILÍNEO VARIADO
f) an=0,
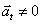 6)
CURVILÍNEO UNIFORME
6)
CURVILÍNEO UNIFORME
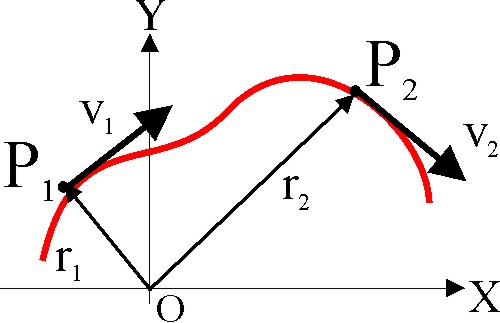
1.2.40.* El movimiento de un punto material,
sigue la trayectoria de la figura. Se podría decir por lo tanto que:
a) EN
P2, LA DIRECCIÓN DEL RADIO DE CURVATURA COINCIDE CON LA DEL VECTOR
DE POSICIÓN
b) EN
P1, EL MÓDULO DE VECTOR DE POSICIÓN COINCIDE CON EL RADIO DE CURVATURA
c) EN
P1, EL SENTIDO DEL VECTOR DE POSICIÓN COINCIDE CON EL DEL RADIO
DE CURVATURA
d) SE
TRATA DE UN MOVIMIENTO CURVILÍNEO VARIADO
e) NADA
DE LO DICHO
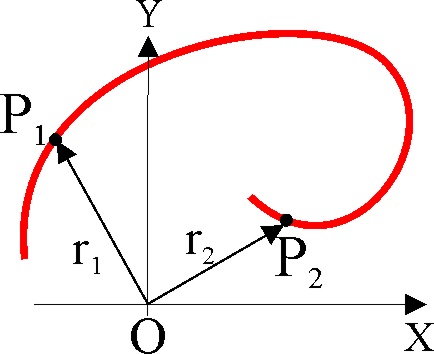
1.2.41.* La trayectoria que se observa en
el dibujo, corresponde al movimiento de un punto material, si se estudia con
detenimiento se podrá asegurar que:
a) EN
P1 LA DIRECCIÓN DEL RADIO DE CURVATURA COINCIDE CON LA DEL VECTOR
DE POSICIÓN
b) EN
P2 LA DIRECCIÓN DEL RADIO DE CURVATURA COINCIDE CON LA DEL VECTOR
DE POSICIÓN
c) EN
P1 EL SENTIDO DEL VECTOR DE POSICIÓN COINCIDE CON EL DEL RADIO
DE CURVATURA
d) EN
P2 EL VALOR DEL MÓDULO DEL VECTOR DE POSICIÓN COINCIDE CON EL VALOR
DEL RADIO DE CURVATURA
e) NADA
DE LO DICHO
1.2.42.* Conociendo el concepto de radio
de curvatura de un movimiento se podrá afirmar
que:
a) SI EL MOVIMIENTO ES RECTILÍNEO
VALE 0
b) SI EL MOVIMIENTO ES RECTILÍNEO
VALE
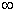
c) SI EL MOVIMIENTO ES CURVILÍNEO NUNCA
SERÁ 0
d) NUNCA SERÁ IGUAL AL VECTOR DE POSICIÓN
e) NADA DE LO DICHO
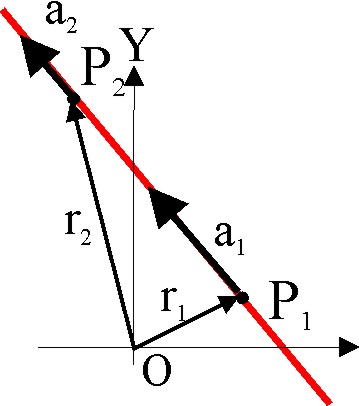
1.2.43.* Si un punto móvil, describiendo la trayectoria
de la figura, pasa de P1 a P2, de forma
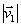 =
=
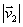 , se podría decir que:
, se podría decir que:
a) LA
ACELERACIÓN ENTRE P1 Y P2 VALE 0
b) LA
ACELERACIÓN EN CUALQUIER PUNTO ENTRE P1 Y P2 SE DIRIGE
HACIA EL ORIGEN DE COORDENADAS
c) EL
MÓDULO DE LA ACELERACIÓN MEDIA ES EL DOBLE DEL DE LA VELOCIDAD
d) EL
RADIO DE CURVATURA ES IGUAL AL MÓDULO DEL VECTOR DE POSICIÓN
e) NADA DE LO DICHO
1.2.44.* Si se trata de calcular matemáticamente
las componentes de la aceleración, se podrá afirmar que la aceleración normal
o centrípeta, surge:
a) AL DERIVAR EL VECTOR UNITARIO DE LA VELOCIDAD
RESPECTO AL TIEMPO
b) AL DERIVAR EL PRODUCTO DEL MÓDULO DEL
VECTOR VELOCIDAD POR SU VECTOR UNITARIO RESPECTO AL TIEMPO.
c) AL DERIVAR EL VECTOR VELOCIDAD RESPECTO
AL TIEMPO
d) AL CONSIDERAR EL CAMBIO DE DIRECCIÓN
Y SENTIDO DEL VECTOR UNITARIO DE LA VELOCIDAD EN EL TIEMPO
e) NADA DE LO DICHO
1.2.45.* Dado que el vector v, se
puede considerar como el producto de un escalar que valga el módulo de v
por un vector unitario en la dirección y sentido de v, de la derivación
respecto al tiempo de este producto, surgen matemática-mente:
a) EL CONCEPTO Y LA FÓRMULA DE LA ACELERACIÓN
TANGENCIAL
b) EL CONCEPTO Y LA FÓRMULA DE LA ACELERACIÓN
NORMAL O CENTRÍPETA
c) EL CONCEPTO DE RADIO DE CURVATURA
d) NADA DE LO DICHO
1.2.46. La constante de integración C, que
surge en el cálculo del vector de posición a través de la expresión
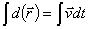 , en un movimiento uniforme
se podría evaluar:
, en un movimiento uniforme
se podría evaluar:
a) CONSIDERANDO LAS CONDICIONES INICIALES
DE r
b) DANDO A t EL VALOR 0
c) CONSIDERANDO LA VELOCIDAD INICIAL, 0
d) CONSIDERANDO LA VELOCIDAD CONSTANTE
1.2.47. La constante de integración C, que
surge al calcular la velocidad en un MUA, por integración de la expresión
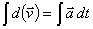 , se podría evaluar:
, se podría evaluar:
a) CONSIDERANDO LAS CONDICIONES INICIALES
DE v
b) DANDO A t EL VALOR 0
c) CONSIDERANDO LA VELOCIDAD INICIAL, 0
d) BASÁNDOSE EN QUE LA ACELERACIÓN SEA
CONSTANTE
1.2.48. La constante de integración C, que
surge al calcular el espacio recorrido por un punto móvil, en un MUA, podría
evaluarse:
a) CONSIDERANDO LAS CONDICIONES INICIALES
DE r O s
b) DANDO A t EL VALOR 0
c) CONSIDERANDO LA ACELERACIÓN Y LA VELOCIDAD
INICIAL, CONSTANTES
d) CONSIDERANDO
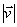 =vi
=vi
1.2.49. Dado que la ecuación del espacio,
o ecuación horaria de un punto material, en un MUA: s=s0+v0t+at2/2
se puede considerar como una ecuación del tipo de: s=C+Bt+At2,
por lo que en una gráfica posición/tiempo (s/t), correspondería a:
a) UNA RECTA QUE PASA POR EL ORIGEN
b) UNA CIRCUNFERENCIA
c) UNA PARÁBOLA
d) UNA ELIPSE
1.2.50. Dado que la ecuación de la velocidad,
en un MUA: v=v0+at, se puede identificar con una del tipo v=A+Bt,
en una gráfica velocidad/tiempo (v/t), correspondería a una:
a) CURVA DE SEGUNDO GRADO
b) UNA PARÁBOLA
c) UNA RECTA PARALELA EL EJE t
d) UNA RECTA QUE PASA POR EL ORIGEN
e) NADA DE LO DICHO
1.2.51.* Teniendo en cuenta que la ecuación
horaria, en un MUA, en un diagrama s/t, corresponde a una parábola, si dicha
ecuación fuera:
s=5t-5t2, se podría decir que
la parábola
a) ES CÓNVEXA
b) ES CÓNCAVA
c) TIENE EL VÉRTICE EN EL PUNTO (0,0)
d) TIENE EL VÉRTICE EN EL CUARTO CUADRANTE
e) NADA DE LO DICHO
Si la ecuación fuera del tipo s=-10t+5t2,
podrías decir entonces que la parábola tiene:
a) LA CONCAVIDAD HACIA ABAJO,O CÓNCAVA
b) LA CONCAVIDAD HACIA ARRIBA,O CONVEXA
c) EL VÉRTICE EN EL PUNTO (0,0)
d) EL VÉRTICE EN EL PRIMER CUADRANTE
e) NADA DE LO DICHO
1.2.52. Dada la ecuación horaria de un móvil:
s=s0+v0t+at2/2, y sabiendo que dicho móvil
tiene una velocidad de 17 m/s a los 4 segundos y que a los 2 y 4 segundos
dista del origen, 12 y 40 metros respectivamente, se asegurará que el espacio
inicial, la velocidad inicial y su aceleración, valen en unidades SI, respectivamente:
a) -4,5,3 b) 4,1,3 c) 8,5,3
d) 0,5,1 e) NADA DE LO DICHO
1.2.53. Sabes que un móvil se desplaza con
movimiento rectilíneo uniformemente acelerado y determinas que en los instantes
1, 2 y 3 segundos ha recorrido respectivamente 70, 90 y 100 metros. Con estos
datos, deducirás que pasará por el origen de los espacios a los:
a) 0,6s b) 7,5s
c) 7s d) 8s
e) NADA DE LO DICHO
1.2.54. Las aceleraciones de cuatro móviles
A, B, C y D son respectivamente 40 km/min2, 20 cm/s2,
104 m/min2 y 15 m/s2. El orden de aceleración
de mayor a menor de los cuatro móviles es:
a) D, A, B, C b) A, B, C, D
c) B, A, D, C d) D, A, C,
B
1.2.55. Un móvil que lleva inicialmente
una velocidad de 14m/s, con aceleración constante, y alcanza una velocidad
de 18 m/s en 10 s. El espacio recorrido en estos 10s será de:
a) [(18-14)/2]·10
m b) [(18+14)/2]·10
m
c) [(14-18)/2]·10
m
d) [(18-14)/2]·2 m
e) [(14-10)/2]·18
m
1.2.56. Si el vector de posición de un punto
material viene dado por la expresión r=t4i-t4j,
se podrá argumentar, que los vectores velocidad y
aceleración forman entre sí un ángulo de:
a)
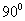 b)
b)
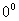 c)
c)
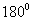 d)
d)
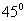
e) NADA DE LO DICHO
1.2.57. Si una partícula se mueve con una
trayectoria parabólica de ecuaciones, y=kx2, z=0 y la componente
y de su velocidad se mantiene constante con un valor b, se dirá que:
a) SE MUEVE EN EL PLANO XZ
b) EL MOVIMIENTO QUE REALIZA ES UN M.U.A
c) LA ACELERACIÓN DEPENDE DE LA POSICIÓN
EN CADA INSTANTE SOBRE EL EJE X
d) EN EL VÉRTICE DE LA PARÁBOLA
LA ACELERACIÓN ES 0
1.2.58. Si un punto material se mueve a
lo largo del eje X, y el módulo de su velocidad viene dado por la expresión
v=t2-2t+4, de forma que cuando
pasa por el origen éste es 3m/s, se podrá decir que su vector de posición
al cabo de 1 segundo es:
a) (10/3)i
b) 0
c) –i
d) i
e) NINGUNO DE LOS VALORES DADOS
1.2.59. Si un punto material se desplaza
sobre la parte positiva del eje X, con una aceleración cuyo módulo es 3t,y
con vectores de posición a los 1 y 2 segundos, respectivamente r1=i, y r2=2i,
se dirá que a los 3s, estará en el punto:
a) (3,0,0) b) (0,0,0)
c) (0,3,0) d) (9,0,0)
e) NINGUNO DE LOS VALORES DADOS
1.2.60. Si un punto material que se desplaza
con movimiento rectilíneo, con una aceleración a=4t2j
m/s2, al cabo de 1 segundo se encuentra a 1m del origen y a los
2 segundos, a 2 metros, el módulo de su vector de posición al cabo de 3 segundos,
será aproximadamente de:
a) 3m
b) 9m
c) 20m
d) 10m
e) NINGUNO DE LOS VALORES DADOS
1.2.61. Si un punto material que estaba
en reposo en el origen, cuando t=0, se desplaza con un movimiento rectilíneo
sobre el eje X, con una aceleración cuyo módulo varía con el tiempo según
la expresión a=[2/(1+t)2] i,
en unidades del SI, dirás que al cabo de 1s, su vector de posición, en metros,
será el:
a) -0,6i b) -3,4i
c) 0,6i d) 3,4i
e) NINGUNO DE LOS
VALORES DADOS
![]()
![]()
![]() VALE 0 PARA t=1s
VALE 0 PARA t=1s