4.2. FUERZAS
Y MOMENTOS EN DINÁMICA DE ROTACIÓN.
4.2.1. El momento de inercia de un cilindro respecto
del eje que pasa por el centro de sus bases es mR2 /2, siendo m
su masa y R el radio. Si se aplica un momento M a un cilindro de masa 0,5
kg y radio 10 cm la aceleración angular resultante es:
a) 4M b) 40M
c) 400M d) 4000M
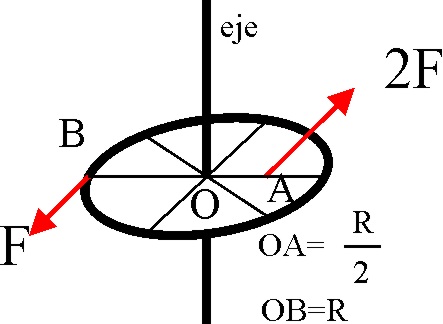
4.2.2. Sobre una rueda de masa m concentrada en la periferia
y radio R, actúan
las fuerzas que se indican en el dibujo; la aceleración angular de la rueda
es:
a) nula b)
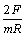
c)
d)
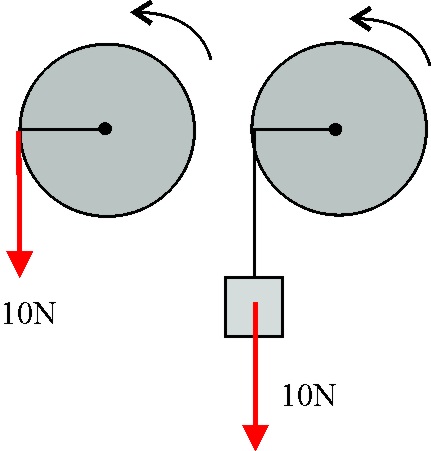
4.2.3. Sobre un mismo cilindro de masa M y radio R pueden
actuar o una fuerza constante de 10N o un peso de 10N, (cuya masa la aproximamos a
a) 1 b) 2
c) 3
d) 1+20R/(Mg)
e) 1+20/(gM)
4.2.4. Por la garganta de una polea fija de radio R pasa
una cuerda de masa despreciable.
De los extremos de la misma se cuelgan dos cuerpos, uno de masa m y el otro
2m. La aceleración con que se desplazan los cuerpos es g/9, por lo que el
momento de inercia de la polea es:
a) 6mR2 b) 14mR2
c) 16mR2 d) 18m2
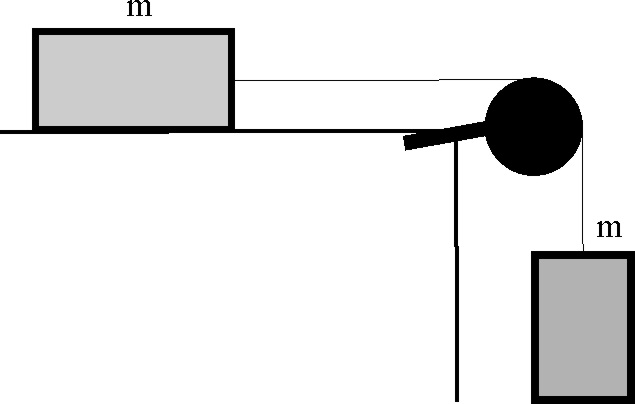
4.2.5. En el sistema de la figura, hay dos masas iguales m unidas por una cuerda que pasa por
una polea, siendo M la masa de la polea y R su radio. La aceleración de
la masa que cuelga es g/4, por consiguiente el momento de inercia de la polea
es:
a) mR2
b) 2mR2
c) 3mR2 d) 4mR2
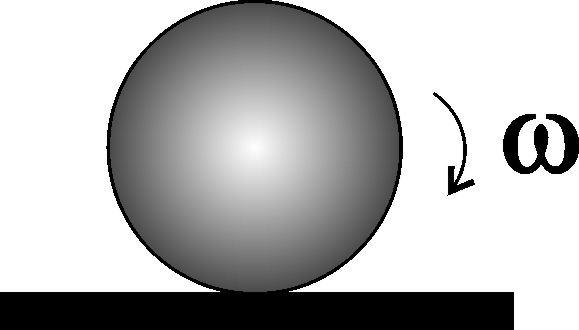
4.2.6*. Una esfera de radio R rueda sin deslizar con ω constante,
por una mesa horizontal:
a) EL PUNTO
EN CONTACTO CON EL SUELO NO TIENE VELOCIDAD NULA
b)
c) EL PUNTO
EN CONTACTO CON EL SUELO TIENE ACELERACIÓN TANGENCIAL.
d) EL PUNTO
EN CONTACTO CON EL SUELO TIENE ACELERACIÓN NORMAL.
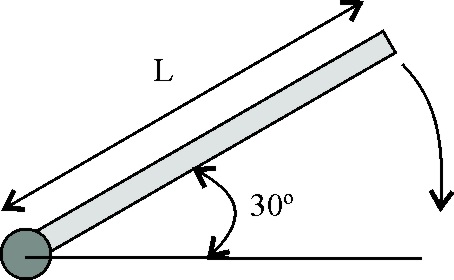
4.2.7. Una varilla uniforme de masa M y longitud L está pivotada
en uno de sus extremos y desde la posición indicada en la figura se deja en
libertad, cuando la varilla pasa por la posición horizontal la aceleración
angular es:
a) g/(2L) b) 3g/(2L) c) 5g/(2L) d) 7g/(2L)
y las reacciones vertical y horizontal de la articulación
son:
e) Mg/4, 3Mg/4 f) Mg, Mg
g) Mg/4, Mg h) 3/4Mg, 1/8Mg
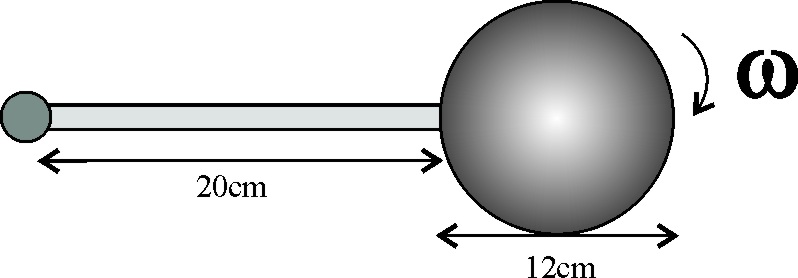
4.2.8. Un sistema está formado por una varilla delgada
y uniforme con una esfera en su extremo, tal como indica la figura. La masa
de la varilla es
a) 39 b)
25 c) 17 d) 8
y las reacciones vertical y horizontal en la articulación
son en N:
e) 12 , 11 f)
20 , 15 g) 15 , 15 h) 40 , 16
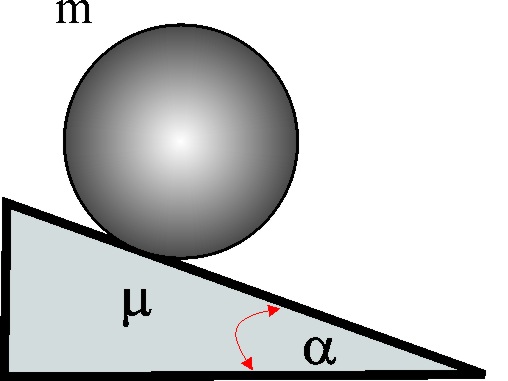
4.2.9.* Cuando un cuerpo de masa m rueda sin deslizar
por un plano inclinado
grados, con el que tiene un coeficiente
de rozamiento
podrás decir que lo hace:
a) POR ACCIÓN
DEL CAMPO GRAVITATORIO
b) DEBIDO
A LAS FUERZAS DE ROZAMIENTO
c) A CONSECUENCIA
DE LA REACCIÓN QUE EJERCE EL PLANO
d) PORQUE
LAS FUERZAS DE ROZAMIENTO SON MENORES QUE
4.2.10.* Euler supuso en 1760, que el movimiento de rodadura de un sólido
por encima de una mesa, se podía descomponer en una rotación simple, en la
que todos los puntos de la periferia tenían un módulo de la velocidad angular constante, y
una traslación en la que todos los puntos tenían el mismo vector velocidad.
Con esta idea:
a) HABRÁ
PUNTOS DE LA PERIFERIA CON VELOCIDAD 0
b) LA VELOCIDAD
DEL CENTRO DE MASAS SIEMPRE ES LA MISMA
c) LA VELOCIDAD
DE UN PUNTO DE LA PERIFERIA PUEDE SER EL DOBLE DE LA DEL CENTRO DE MASAS
d) LA TRAYECTORIA
DE UN PUNTO DE LA PERIFERIA ES UNA CIRCUNFERENCIA
4.2.11. La aceleración de un punto de la periferia de
una esfera que rueda por una mesa:
a) SÓLO
TIENE COMPONENTE TANGENCIAL
b) SÓLO
TIENE COMPONENTE NORMAL
c) SÓLO
PUEDE SER ANGULAR
d) ES NULA
SI LA VELOCIDAD DEL CENTRO DE MASAS ES CONSTANTE
e) TIENE
COMPONENTE NORMAL Y TANGENCIAL, SI LA vCM NO FUERA CONSTANTE
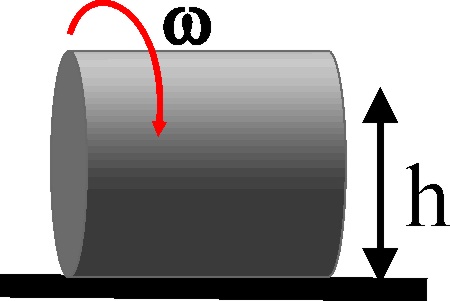
4.2.12. Cuando un cuerpo rueda sin deslizar por una mesa,
con velocidad angular constante, podrás decir que todos los puntos situados
a igual altura h sobre dicha mesa tienen:
a) EL MISMO
VALOR DE LA VELOCIDAD LINEAL
b) LA MISMA
VELOCIDAD ANGULAR
c) LA MISMA
ACELERACIÓN TANGENCIAL
d)
e)
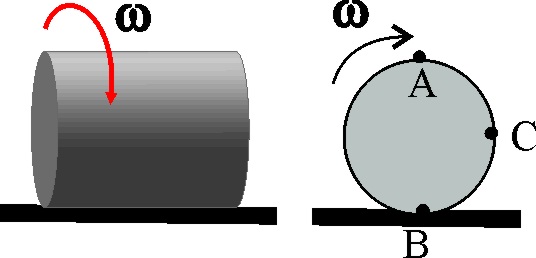
4.2.13. Un cilindro de radio R, cuyo corte aparece en
la figura, rueda sin deslizar sobre una mesa, con w = cte. Respecto de los puntos , A, B y C, podrás decir
que:
a) LA VELOCIDAD
ANGULAR DE B SIEMPRE ES 0
b) LA VELOCIDAD
LINEAL DE C ES DOBLE QUE LA DE B
c) EL MÓDULO
DE LA ACELERACIÓN NORMAL DE A ES IGUAL A LA DE B
d) LA ACELERACIÓN
DE A ES DOBLE QUE LA DE B
4.2.14. En el estudio de la dinámica de
rotación de un cuerpo es muy importante el concepto de eje instantáneo de
rotación. Si supones una esfera que rueda sin deslizar
por una mesa, su eje instantáneo será un eje:
a)
QUE PASA POR EL CENTRO DE MASAS PARALELO AL SUELO Y PERPENDICULAR A
b)
QUE PASA POR EL PUNTO DE CONTACTO CON EL SUELO Y ES PERPENDICULAR AL MISMO
c)
QUE PASA POR EL PUNTO DE CONTACTO Y
ES PARALELO AL SUELO
d)
LUGAR GEOMÉTRICO DE TODOS LOS PUNTOS CUYA VELOCIDAD ES CERO
e)
PERPENDICULAR AL SUELO PASANDO POR EL CENTRO DE MASAS Y POR EL PUNTO DE CONTACTO
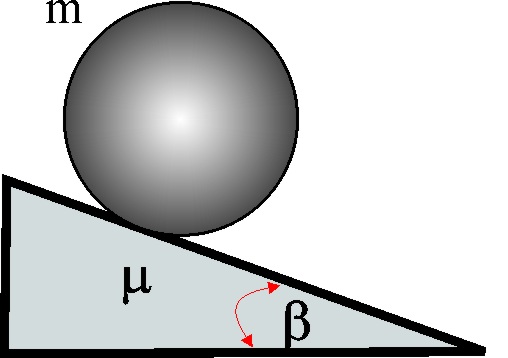
4.2.15. Si queremos que una esfera de radio R, y masa
m, ruede sin deslizar por un plano inclinado, con el cual tiene un coeficiente
de rozamiento por deslizamiento de 0,2 hace falta
que el ángulo de dicho plano
sea menor de:
a)
b)
c)
d)
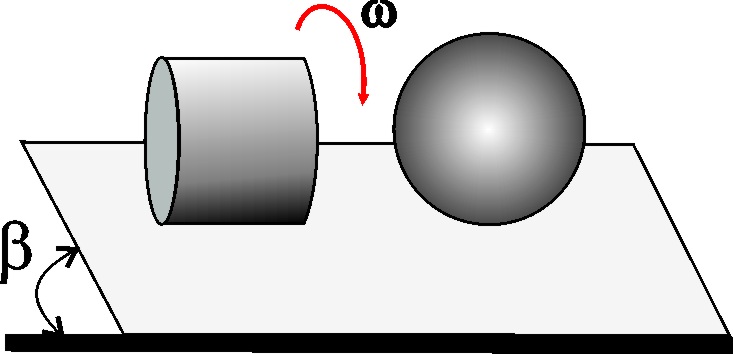
4.2.16. Situados una esfera y un cilindro de la misma
masa, en lo alto de un plano inclinado un ángulo
, al dejarlos libres empiezan a rodar.
a)
b)
c) SEA CUALQUIERA
EL VALOR DE b SIEMPRE
HABRÁ RODADURA SIN DESLIZAMIENTO
d)
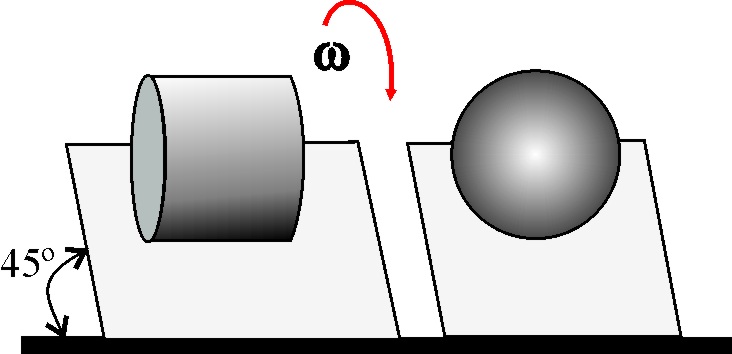
4.2.17. Situamos una esfera sobre un plano inclinado
45º en condiciones tales que ruede sin deslizar, y luego repites el hecho
con un cilindro del mismo material y radio. Para conseguir la misma circunstancia,
necesitarás disminuir el ángulo en aproximadamente:
a) 4º
b) 10º c) 15º d) 20º
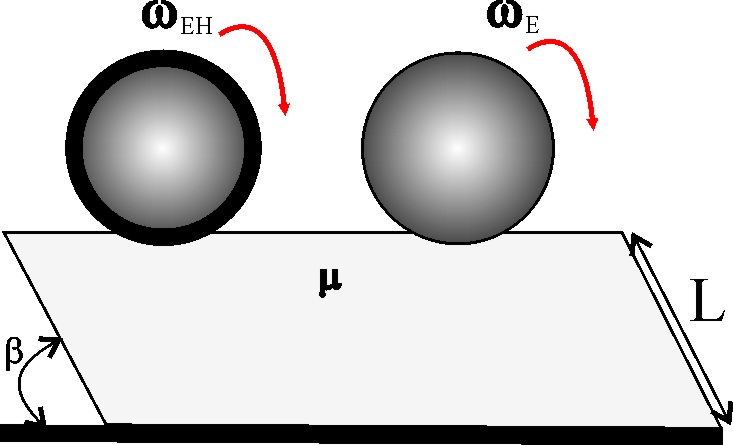
4.2.18. Si sitúas una esfera hueca EH(corteza esférica)
y otra maciza E, del mismo material y radio, sobre lo alto de un plano inclinado
de longitud L, si ambas ruedan por él sin deslizar siendo el coeficiente de
rozamiento m= 0,2, dirás
que:
a) LA FUERZA
DE ROZAMIENTO SOBRE LA HUECA ES MAYOR QUE LA MACIZA PARA UN MISMO ANGULO DEL
PLANO INCLINADO
b) EL ÁNGULO
MÍNIMO DEL PLANO INCLINADO EN LA MACIZA ES EL DOBLE QUE EN LA HUECA
c) LA VELOCIDAD
CON QUE LLEGA A LA BASE LA HUECA ES DOBLE QUE LA DE LA MACIZA
d) CUANDO
