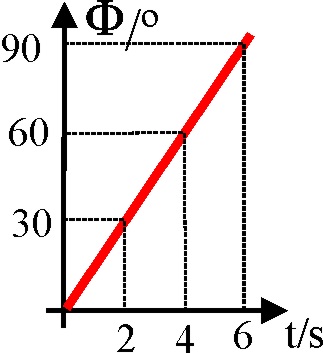
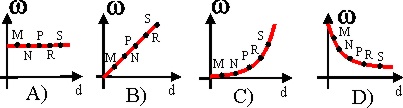
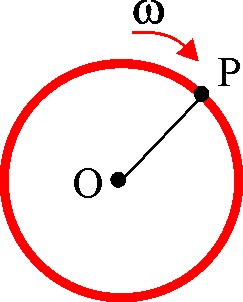
1.6.12. Si
un ciclista se mueve por la pista de un velódromo de radio 50m con una aceleración
tangencial constante, de 1 m/s2, el tiempo que tardará desde
que comienza a moverse hasta que su aceleración normal sea la mitad de la tangencial será de:
a)
2s b) 3,5s c) 5s
d)
4,2s e)10s
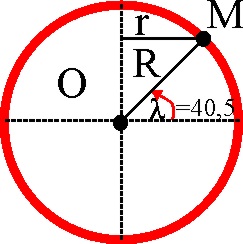
1.6.13. Una
rueda a los dos segundos de comenzar su movimiento, tiene una aceleración
total que forma un ángulo de
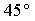 con su velocidad tangencial , se deduce que la aceleración angular vale:
con su velocidad tangencial , se deduce que la aceleración angular vale:
a) 1 rad/s2 b) 0,5 rad/s2
c) 0,25 rad/s2 d) 2 rad/s2
e) NINGUNO
DE LOS VALORES DADOS
1.6.14.* En
una pista experimental circular de 1m de radio de un laboratorio, una esfera
se desplaza sin rozamiento de forma que el camino recorrido sigue la ley
s=3t3, en estas circunstancias podrás decir que:
a) LA ESFERA SE MUEVE CON UN MOVIMIENTO UNIFORMEMENTE
ACELERADO
b) LA ACELERACIÓN NORMAL SIEMPRE SERÁ CONSTANTE
c) CUANDO LA VELOCIDAD TANGENCIAL ES DE 9 m/s, LA
ACELERACIÓN TANGENCIAL VALE 18 m/s2
d) CUANDO LA VELOCIDAD TANGENCIAL ES DE 3 m/s, LA
ACELERACIÓN NORMAL ES DE 81 m/s2
e) EL VECTOR DE POSICIÓN TIENE UN MÓDULO CONSTANTE
1.6.15. Las
ruedas de un camión de 40 cm de radio giran de forma que un chicle pegado
a la llanta tiene una velocidad lineal que sigue la ley v=3t+t2 cm/s.
Con este dato podrás deducir que el ángulo que forma el vector de posición
del chicle respecto al eje de la rueda, y su vector aceleración en el instante
t=1s es:
a) SIEMPRE
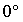 Y ES INDEPENDIENTE DEL TIEMPO
Y ES INDEPENDIENTE DEL TIEMPO
b) SIEMPRE
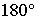 EN CUALQUIER INSTANTE
EN CUALQUIER INSTANTE
c)
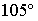
d)
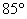
e)
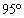
1.6.16. Si
un punto material se mueve con unas ecuaciones paramétricas x=2·sent, y=2·cost,
dirás que la ecuación de la hodógrafa será:
a) UNA RECTA DE PENDIENTE
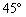
b) UNA RECTA QUE PASA POR EL PUNTO (2,2)
c) UNA CIRCUNFERENCIA DE RADIO 2
d) UNA CIRCUNFERENCIA DE RADIO 4
e)NADA DE LO DICHO
1.6.17. Si
un punto material se mueve con un vector de posición r=3·costi+4·sentj,
dirás que la ecuación de la hodógrafa será:
a)
UNA CIRCUNFERENCIA DE RADIO 5
b)
UNA CIRCUNFERENCIA DE RADIO 25
c)
UNA ELIPSE DE SEMIEJES 3 Y 4
d)
UNA ELIPSE DE SEMIEJES 9 Y 16
e)
UNA PARÁBOLA
1.6.18. Dado
el vector de posición de un punto material, r=4·cos
 ti+ 4·sen
ti+ 4·sen
 tj + 4k, su aceleración, si la tiene, formará con él un ángulo
de:
tj + 4k, su aceleración, si la tiene, formará con él un ángulo
de:
a)
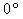 b)
b)
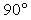
c)
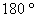 d)
d)
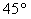
e) NADA DE
LO DICHO
1.6.19.* Si
un punto se mueve de forma que las ecuaciones paramétricas son: x=a·senbt,
y=a·cosbt, z=ct, dirás de él que:
a) DESCRIBE UN MOVIMIENTO HELICOIDAL
b) EL MÓDULO DE SU VELOCIDAD DEPENDE DEL TIEMPO
c) SU ACELERACIÓN TANGENCIAL ES 0
d) SU VECTOR ACELERACIÓN VALE ab2
1.6.20.* Si
el vector de posición de un punto que describe un movimiento helicoidal
es r=2·cos4ti+2·sen4tj+2tk, en el SI, podrás
asegurar que:
a) SU VELOCIDAD NO DEPENDE DEL TIEMPO
b) SU ACELERACIÓN TANGENCIAL ES IGUAL A LA NORMAL
c) EL MÓDULO DE LA ACELERACIÓN ES CONSTANTE
d) SU RADIO DE CURVATURA VALE APROXIMADA-MENTE 2
METROS
1.6.21.* Si
un móvil recorre una circunferencia de 20m de radio, a partir del punto
P(20,0),de forma que el camino recorrido a través de ella sigue una ley
s=20 cos
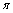 t , podrás decir de él que a los 3 segundos de iniciado el movimiento:
t , podrás decir de él que a los 3 segundos de iniciado el movimiento:
a) SU ACELERACIÓN NORMAL ES NULA
b) EL MÓDULO DE SU ACELERACIÓN TANGENCIAL ES 20
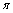 2 m/s2
2 m/s2
c) EL ÁNGULO QUE FORMAN SU VELOCIDAD Y EL RADIO
DE CURVATURA ES DE
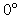
d) EL ÁNGULO QUE FORMAN SU ACELERACIÓN Y EL RADIO
DE CURVATURA ES DE
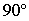
![]() siendo el radio de 2
m, habrá recorrido una longitud de:
siendo el radio de 2
m, habrá recorrido una longitud de:![]() b)
b)
![]() c)
12 m
c)
12 m![]() c) 60·2 m
c) 60·2 m