ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
1.5. CINEMÁTICA
DEPORTIVA
1.5.1.* El
14 de agosto de 1991, se produjo, en Tokio, un hecho deportivo realmente curioso,
ya que aparte de batirse un record del mundo de velocidad en carrera, 6 atletas
corrieron los 100 metros lisos en menos de 10 segundos. Dadas las posiciones
instantáneas de los corredores, desde la calle 2 a la 7, podrás asegurar que:

a) EL ATLETA QUE TARDÓ MAS TIEMPO EN REACCIONAR
DESPUÉS DEL PISTOLETAZO DE SALIDA ES EL DE LA CALLE 3
b) EL QUE LLEVA UN MOVIMIENTO MAS REGULAR ES EL
DE LA CALLE 6
c) LA ACELERACIÓN MAYOR EN UN DETERMINADO INTERVALO
LA TIENE EL DEPORTISTA DE LA CALLE 4
d) APROXIMADAMENTE EL DE MAYOR VELOCIDAD INSTANTÁNEA
SERÁ EL DE LA CALLE 3
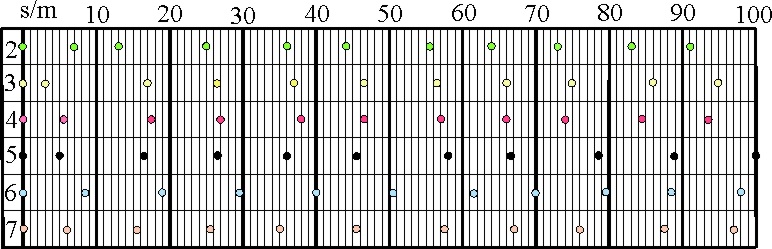
1.5.2.* Carl
Lewis, batió el record del mundo de los 100 metros lisos en los campeonatos
del mundo celebrados el verano de 1991, en Tokio. En la tabla dada, se relacionan
las posiciones, tiempos y velocidades en el SI, de dicho atleta en la carrera:
| |
O |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
| s /m |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
| t/s |
0 |
1,2 |
2,3 |
3,3 |
4,3 |
5,2 |
6,1 |
7,1 |
8,0 |
8,9 |
9,86 |
| v/ms-1 |
0 |
8,33 |
8,69 |
9,09 |
9,30 |
9,61 |
9,84 |
9,86 |
10,00 |
10,10 |
10,14 |
Si realizas
una gráfica s/t y v/t , podrás asegurar que:
a) LA MÁXIMA ACELERACIÓN LA TUVO AL LLEGAR A LA
META
b) EN EL TRAMO AC LLEVÓ UN MOVIMIENTO UNIFORME
c) LA ACELERACIÓN MAYOR ES DE 6,94 m/s²
d) EN EL ÚLTIMO TRAMO DE LA CARRERA DISMINUYÓ SU
ACELERACIÓN
1.5.3. En
una carrera de 100 m lisos, un bromista mal intencionado carga la pistola
del juez de salida, con un cartucho de poco peso. El juez se sitúa inmediatamente
detrás de la calle 1 y dispara, casi verticalmente para indicar la salida
a los atletas, con tan mala suerte que al vencedor, corriendo en la calle
1 y que tarda 10s en alcanzar la meta, le cae en ese instante y en la cabeza
el chasis del cartucho dejándolo sin sentido. Con estos datos podrás decir
que el ángulo con que disparó la pistola es de:
a)
![]() b)
b)
![]() c)
c)
![]()
d)
![]() e) NADA DE LO DICHO
e) NADA DE LO DICHO
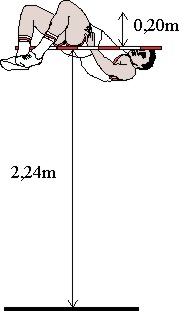
1.5.4. En
la olimpiada de México, en 1968, un atleta americano, Fosbury creó una nueva
técnica de salto de altura que le permitió ganar con aparente poco esfuerzo
la medalla de oro, debido a que su centro de gravedad pasaba muy cerca del
listón, y por lo tanto, al ser menor la altura necesaria para sobrepasarlo,
el impulso sería también menor. Si su centro de gravedad estaba a 1,2 m y
debería pasar 20 cm por encima del listón puesto a 2,24 m, la componente vertical
de su velocidad de impulso debería ser de:
a) 5,21 m/s b)
4,93 m/s c) 4,81 m/s
d)
5,0 m/s e) NINGUNO
DE LOS VALORES DATOS
Tómese g=9,8 m/s2
1.5.5. Muchas
veces cuando juegas a la pelota en la playa, si es suficientemente ligera,
te la lleva el viento. Por eso al lanzarla verticalmente si luego pretendes
darle de cabeza, tienes que desplazarte bastante. En todo caso, la trayectoria
que seguiría si la velocidad del viento lateral es uniforme y su módulo es
la mitad del que tiene tu velocidad
de lanzamiento v, sería:
a) UNA RECTA CUYA PENDIENTE SERÍA 1/2
b) UNA PARÁBOLA CUYO VÉRTICE SERÍA EL PUNTO (v2/2g;
v2/2g)
c) UNA PARÁBOLA CUYO VÉRTICE SERÍA EL PUNTO (v2/2g;
v2/g)
d) UNA RECTA QUE FORMA UN ÁNGULO DE
![]() CON LA HORIZONTAL
CON LA HORIZONTAL
1.5.6*. La
proeza deportiva más grande que se consiguió en 1991, fue superar la mejor
marca mundial de salto de longitud, realizada por Beamon en la olimpiada de
México. El atleta americano Powell fue el encargado del hecho, saltando 8,95
m, con un viento a favor de 0,3 m/s (el factor corrector de la velocidad del
viento sobre la del atleta es aproximadamente de 0,1), y sobrepasando la marca
olímpica en 5 cm. Si su centro de gravedad se encuentra en el momento de saltar
a 1,30m y que al caer queda a 10 cm del suelo despegando inicialmente de éste
con un ángulo de 25 grados, podrás decir que:
a) SI NO TUVIERA EL VIENTO A FAVOR NO HUBIERA SUPERADO
EL RECORD DE BEAMON
b) EL MÓDULO DE LA VELOCIDAD CON QUE SE IMPULSÓ
ERA APROXIMADAMENTE DE 9,3 m/s
c) HABRÍA PODIDO BATIR EL RECORD DE LOS 100m LISOS
SI HUBIERA MANTENIDO LA VELOCIDAD DE IMPULSIÓN, EN ESA DISTANCIA
d) SIN VIENTO TAMBIÉN HUBIERA SUPERADO LA MARCA
DE LEWIS REALIZADA MOMENTOS ANTES DE 8,91 m
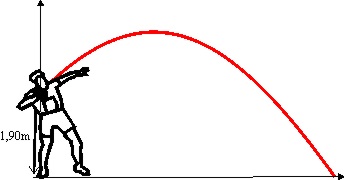
1.5.7. Un
fornido atleta, en Barcelona 92, pretende batir el record del mundo de lanzamiento
de peso. Sabe que el alcance máximo se consigue con un ángulo de
![]() , e impulsa el peso desde 1,90 m. En estas condiciones, y queriendo sobrepasar
los 23 m, deberá impulsarlo con una velocidad mínima cuyo módulo será, en
m/s:
, e impulsa el peso desde 1,90 m. En estas condiciones, y queriendo sobrepasar
los 23 m, deberá impulsarlo con una velocidad mínima cuyo módulo será, en
m/s:
a) 14,6
b) 13,6 c) 15,6
d) 16,6
e) NINGUNO DE LOS VALORES DADOS
1.5.8. En
unas olimpiadas un atleta lanza la jabalina con un ángulo de
![]() , desde una altura sobre el suelo de 2 m. Sabiendo que quiere batir el record
del mundo, haciendo 97 m, en ausencia de viento, y sin contar con el rozamiento
del aire, la velocidad de lanzamiento deberá ser en m/s:
, desde una altura sobre el suelo de 2 m. Sabiendo que quiere batir el record
del mundo, haciendo 97 m, en ausencia de viento, y sin contar con el rozamiento
del aire, la velocidad de lanzamiento deberá ser en m/s:
a) 12i+12j b) 22i+22j
c) 12i-12j
d) 22i-22j e) NINGUNO DE LOS VALORES DADOS
1.5.9. En
un partido de fútbol, situado el balón en el punto A, un delantero lo impulsa
con una velocidad de 8 m/s, formando un ángulo de
![]() con la horizontal. Si no se tienen
en cuenta la resistencia del aire ni el viento, el balón deberá llegar a B,
que dista de A:
con la horizontal. Si no se tienen
en cuenta la resistencia del aire ni el viento, el balón deberá llegar a B,
que dista de A:
a) 2,4 m
b) 4,8 m c) 2,8 m
d) 5,6 m
e) NADA DE LO DICHO
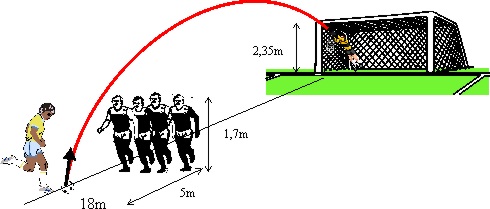
1.5.10. En
cierto partido de futbol, el árbitro pita falta castigando al equipo con un
libre directo. El lugar de la falta se encuentra a 18 m de la base de uno
de los postes de la portería. Por un descuido arbitral, la barrera, integrada
por jugadores de una altura media de 1,70 m, se forma sólo a 5 m del lanzador
del castigo. Para salvar la barrera el jugador que lanza la falta impulsa
el balón con un ángulo de
![]() con la horizontal. Si pretende sortearla
introduciendo el balón por la escuadra (2,35 m) de aquel poste,tendrá
que impulsar el balón, en ausencia de viento, con una velocidad inicial en
m/s, que tiene por módulo:
con la horizontal. Si pretende sortearla
introduciendo el balón por la escuadra (2,35 m) de aquel poste,tendrá
que impulsar el balón, en ausencia de viento, con una velocidad inicial en
m/s, que tiene por módulo:
a) 25
b) 16,3 c) 15,2
d) 24,5 e) NINGUNO DE LOS VALORES DADOS
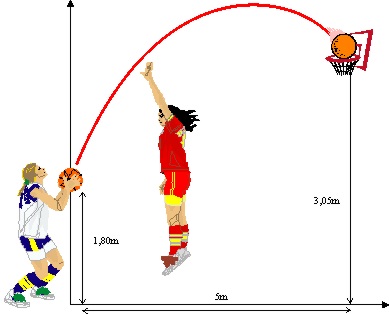
![]() , que lanza desde 1,80 m y que ésta se encuentra a 3,05 m del suelo, podrías
asegurar que una jugadora contraria situada 2 m delante de la canasta y
saltando hasta 2,20m en el momento preciso:
, que lanza desde 1,80 m y que ésta se encuentra a 3,05 m del suelo, podrías
asegurar que una jugadora contraria situada 2 m delante de la canasta y
saltando hasta 2,20m en el momento preciso:
a) CONSEGUIRÍA IMPEDIR LA CANASTA
b) PRODUCIRÍA UN TAPÓN EN TRAYECTORIA DESCENDENTE
CON CANASTA VÁLIDA
c) NO CONSEGUIRÍA IMPEDIR EL LANZAMIENTO
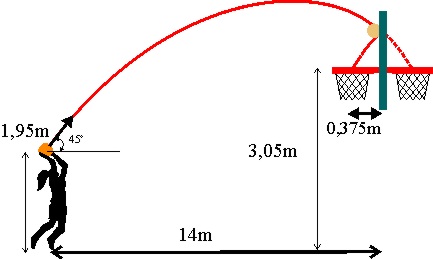
1.5.13.* Faltan
4 segundos para terminar el partido de baloncesto y el equipo de casa pierde
de 2 puntos, pero saca de fondo. El base lanza desde 14 metros a tablero,
en suspensión, desde 1,95 m de altura, y con un ángulo de
![]() , entrando en la canasta después del choque que se supone elástico. Con
los datos que te dan (canasta a 3,05 m de altura, con centro a 0,375 cm
del tablero), podrás afirmar que:
, entrando en la canasta después del choque que se supone elástico. Con
los datos que te dan (canasta a 3,05 m de altura, con centro a 0,375 cm
del tablero), podrás afirmar que:
a) LA TRAYECTORIA DEL BALÓN DESDE EL TABLERO A LA
CANASTA ES RECTILÍNEA
b) LA VELOCIDAD CON QUE IMPULSÓ EL BALÓN FUE DE
12,35 m/s
c) EL BALÓN CHOCA CON EL TABLERO EN SU TRAYECTORIA
ASCENDENTE
d) EL FINAL DEL ENCUENTRO SE PRODUCE ANTES DE QUE
SE CONSIGA LA CANASTA
e) EL BALÓN GOLPEA AL TABLERO A 3,35 m DEL SUELO
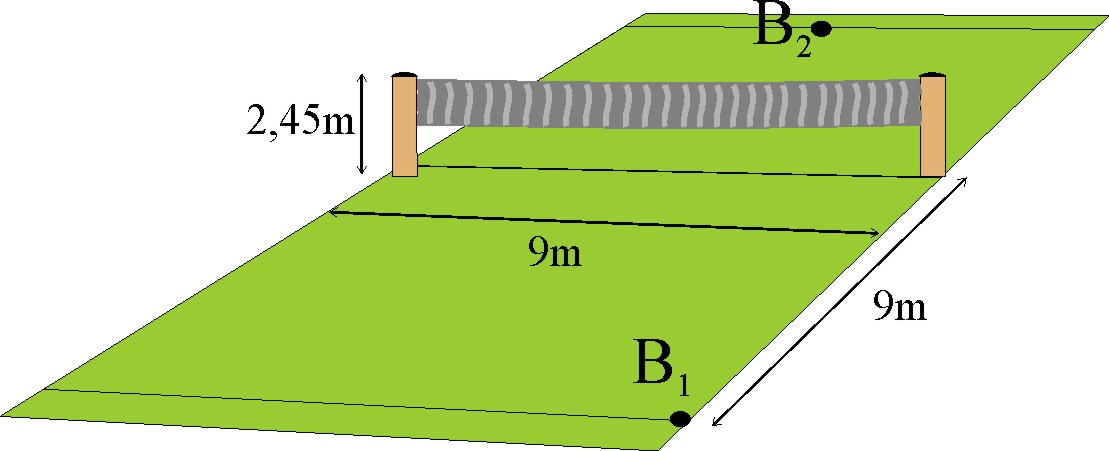
1.5.14.* En
un partido de volei, desarrollado en el campo dado en el dibujo, y con las
dimensiones indicadas, el saque lo ejecuta desde el punto B1
un determinado jugador, impulsando la pelota desde 1,5 m de altura con un
ángulo de
![]() , y tal velocidad que el balón golpea en el punto B2, en el medio
del límite del campo contrario. Con los datos dados podrás asegurar que:
, y tal velocidad que el balón golpea en el punto B2, en el medio
del límite del campo contrario. Con los datos dados podrás asegurar que:
a) LA TRAYECTORIA QUE DESCRIBE ES CIRCULAR
b) EL BALÓN TROPEZARÍA EN LA RED
c) EL BALÓN PASA A MÁS DE 3 m POR ENCIMA DE LA RED
d) LA VELOCIDAD CON QUE DEBE IMPULSAR EL BALÓN EL
LANZADOR TIENE POR MÓDULO 13,5 m/s
e) TOMANDO UN SISTEMA DE EJES EN EL PLANO DEL LANZAMIENTO
CON ORIGEN EN EL PUNTO B1, EL VECTOR VELOCIDAD DE LANZAMIENTO
SERÁ EL 13,5i+13,5j
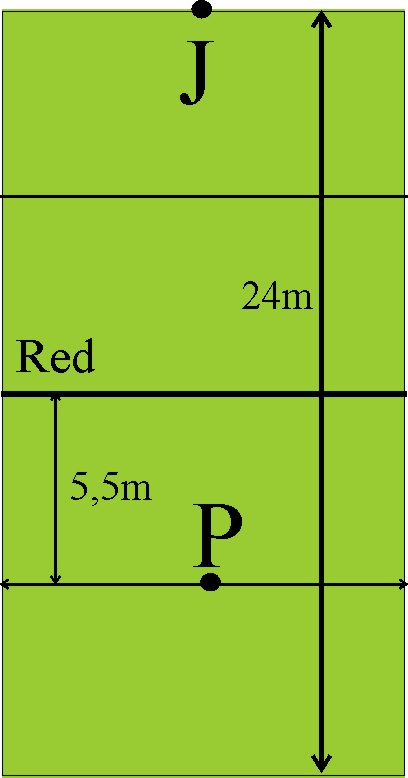
1.5.15.* En
un partido de tenis, un determinado jugador situado a 12m de la red, pretende
hacer un tanto de saque (ace), para lo cual piensa que lo mejor es lanzar
la bola de forma que bote en el suelo en la posición P del esquema dado
a 5,5 m de la red y en campo contrario, y para ello, golpea con la raqueta
la pelota a 2,30 m de altura, formando un ángulo de
![]() con la horizontal y con una velocidad
de 108 km/h, pero la red se levanta hasta 90 cm de altura. Por todo ello,
dirás que:
con la horizontal y con una velocidad
de 108 km/h, pero la red se levanta hasta 90 cm de altura. Por todo ello,
dirás que:
a) SI REDUJESE SU VELOCIDAD DE SAQUE EN UN 30%,
LA PELOTA NO PASARÍA LA RED
b) EL JUGADOR CONSEGUIRÁ EL ACE EN LAS CONDICIONES
INICIALES
c) LA PELOTA PASARÁ A 15 cm POR ENCIMA DE LA RED
d) LA PELOTA GOLPEARÁ EL SUELO CON UNA VELOCIDAD
CUYO MÓDULO ES 5,83 m/s
e) EL ÁNGULO QUE FORMA LA PELOTA AL CHOCAR CON EL
SUELO SERÁ APROXIMADAMENTE DE
![]()
1.5.16.* Suele
decirse que en el tenis para sacar con más seguridad, y no incurrir en la
doble falta, debes golpear la pelota con un ángulo de
![]() por debajo de la horizontal, sin
embargo si a las condiciones de lanzamiento especificadas en la cuestión
anterior (v=108km/h), le aplicas esta circunstancia, te encontrarías que:
por debajo de la horizontal, sin
embargo si a las condiciones de lanzamiento especificadas en la cuestión
anterior (v=108km/h), le aplicas esta circunstancia, te encontrarías que:
a) NO PODRÍAS CONSEGUIR EL PUNTO
b) NO CONSEGUIRÍAS DARLE LA VELOCIDAD ADECUADA
c) LA PELOTA GOLPEARÍA CONTRA LA RED
d) LA PELOTA PASARÍA LA RED PERO GOLPEARÍA EL SUELO
FUERA DE LA LÍNEA DE SAQUE
e) LA PELOTA
ROZARÍA LA RED
1.5.17. Un
jugador de golf, necesita acercarse perentoriamente al hoyo, por lo cual
debe conseguir el alcance máximo, cuando golpea a la bola, pero se encuentra
en una ladera inclinada a su favor, cierto ángulo
![]() , por eso el ángulo sobre la horizontal con que deberá enviar la bola deberá
ser de:
, por eso el ángulo sobre la horizontal con que deberá enviar la bola deberá
ser de:
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
1.5.11. En
el torneo de las 5 naciones de Rugby, un determinado jugador, desde la línea
de 25 yardas (23 m), pretende culminar un ensayo, lanzando el balón por encima
del listón a 3 m. Si el ángulo con que golpea el balón es de
![]() , la velocidad mínima para convertirlo, será aproximadamente, en m/s, de:
, la velocidad mínima para convertirlo, será aproximadamente, en m/s, de:
a) 20
b) 18 c) 16
d)14
e) NINGUNO DE LOS VALORES DADOS