Choque I

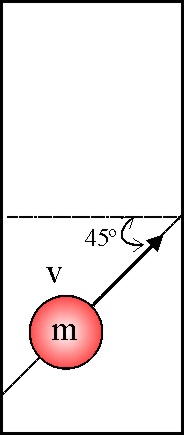
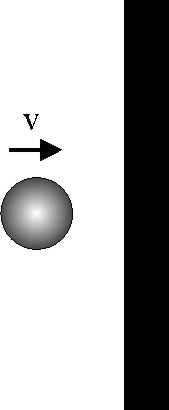
3.5.5.El comportamiento ideal de las moléculas de los gases implica que no existen fuerzas de interacción entre ellas y que sus colisiones son perfectamente elásticas. La presión que ejerce un gas es una manifestación de dichas colisiones. Si una molécula de masa m, y módulo de su velocidad v, colisiona formando un ángulo de , con la pared del recipiente que la contiene, dirás que la variación de su cantidad de movimiento en la colisión tiene por módulo:

a) 2mv b) mv c) 0 d) mv

3.5.6. El primer reactor nuclear, comenzó a funcionar debajo de un campo de rugby, en Chicago, el 2 de diciembre de 1942. La frase clave que dirigió el director del proyecto, Enrico Fermi al presidente Roosvelt fue: "El navegante italiano ha penetrado en el nuevo mundo". 50 años después y no cinco siglos, se puede recordar que los neutrones para que pudieran fisionar los núcleos de uranio, debían colisionar con los de carbono en la forma de grafito (moderador del reactor), cuya masa era doce veces mayor, para frenar su velocidad, de 10.000 km/s a 600km/s. Si el frenado de los neutrones se produjo por colisión elástica con los núcleos de carbono, el número de colisiones sucesivas frontales y perfectamente elásticas para lograrlo serían:

a) 17 b) 15 c) 6 d) 100

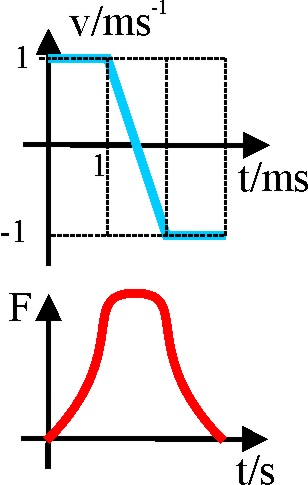
3.5.7*.Si una esfera de acero de masa m, con una velocidad de 1m/s, choca frontalmente contra una pared del mismo material, y las fuerzas elásticas que intervienen durante la colisión así como la velocidad de la esfera, varían según las gráficas dadas, podrás asegurar que :

a) EL CHOQUE FUE PERFECTAMENTE ELÁSTICO

b) LA DURACIÓN DEL CHOQUE FUE DE 0,001 s

c)LA VARIACIÓN DE LA CANTIDAD DE MOVIMIENTO ES DE 2m kg.m/s

d)LA FUERZA MEDIA CON QUE GOLPEÓ LA ESFERA A LA PARED FUE DE 1000N

e)EL MÓDULO DE LA FUERZA MEDIA ES LA SUPERFICIE ABARCADA POR LA CURVA DE LA GRÁFICA /t , DIVIDIDA POR EL TIEMPO

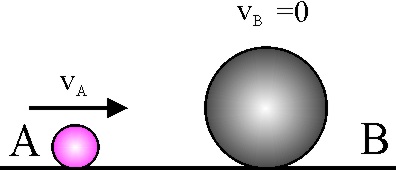
3.5.8.Si un cuerpo A de masa m₁ choca , con otro B, en reposo, de masa m₂, y éste a causa de la colisión elástica y frontal comienza a moverse con una velocidad que es la mitad de la que tenía A, podrás asegurar que la masa de A es:

a) EL DOBLE QUE LA DE B b) EL TRIPLE DE LA DE B

c) LA MITAD QUE LA DE B d) LA TERCERA PARTE QUE LA DE B

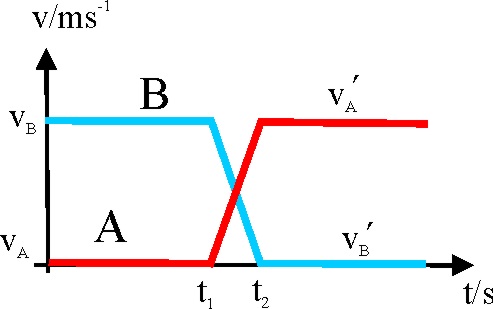
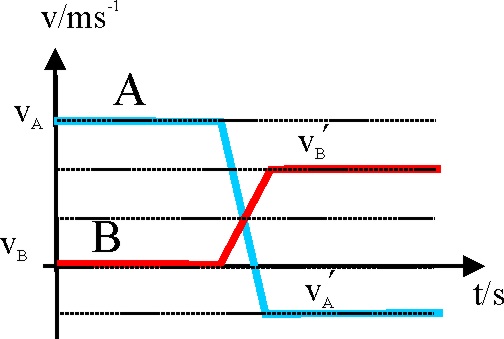
3.5.9.La gráfica v/t dada hace referencia a la variación de las velocidades con el tiempo de dos cuerpos A y B, que colisionan frontalmente. El análisis de la misma así como la aplicación de los conocimientos que ya posees sobre la física del choque de cuerpos te hará asegurar que :

a) EL CHOQUE SE PRODUJO EN EL INTERVALO DE TIEMPO t₂-t₁

b) LA COLISIÓN FRONTAL ES PERFECTAMENTE ELÁSTICA

c) EL CHOQUE FUE FRONTAL PARCIALMENTE INELÁSTICO

d) LA MASA A ES IGUAL A LA DE B

3.5.10.Dada la gráfica v/t de dos cuerpos móviles A y B de masas m₁ y m₂ ,en un referencial de laboratorio que colisionan frontal y elásticamente, podrás asegurar que la relación de sus masas es :

a) LA MITAD b) LA TERCERA PARTE

c) EL DOBLE d) EL TRIPLE

e) NADA DE LO DICHO

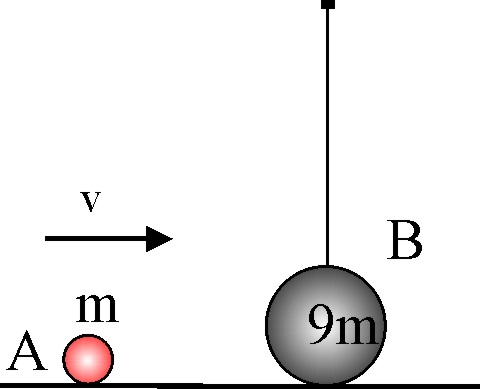
3.5.11.Si un cuerpo A de masa m choca con otro B, en reposo, de masa 9m, de forma frontal y perfectamente inelástica podrás asegurar que en el choque:

a) A SE PARA Y B SE MUEVE

b) A TRASMITE A B ES LA DÉCIMA PARTE DE LA ENERGÍA QUE TENÍA

c) A DISMINUYE SU VELOCIDAD HASTA UN DÉCIMO DE LA QUE TENÍA

d) LA ENERGÍA EMPLEADA EN TRABAJO DE DEFORMACIÓN ES 9/10 DE LA QUE TENÍA A

3.5.12.Si un cuerpo A de masa m y velocidad 2 , choca frontal inelásticamente con B, de masa 9m y velocidad , la energía empleada en trabajo de deformación será respecto a la que tenía inicialmente A:

a) EL DOBLE b) LA MITAD

c) EL CUÁDRUPLE d) LA QUINTA PARTE

e) NADA DE LO DICHO

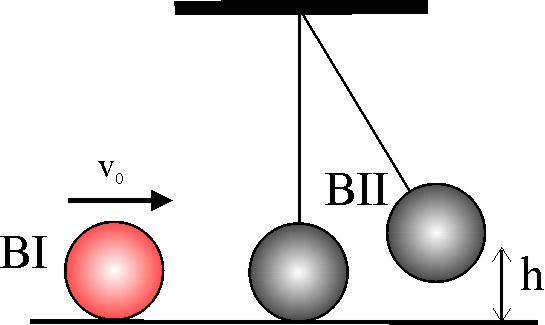
3.5.13. Si el bloque I de la figura lanzado con una velocidad y con coeficiente de rozamiento con el suelo prácticamente despreciable, colisionan elásticamente con el bloque II, de la misma masa suspendido de un hilo inextensible, al mismo nivel que I, la altura h a la que asciende aquél, vendrá dada por la expresión:

a) v₀²/8g b) v₀²/4g c) v₀²/2g d) v₀²/2mg

e) NADA DE LO DICHO

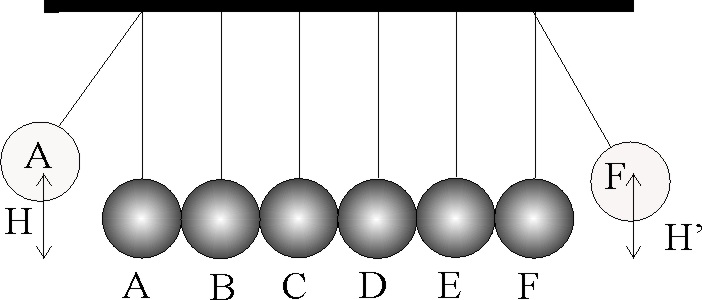
3.5.14.En la introducción de cierto programa de televisión habrás podido observar como, si en una serie de péndulos iguales y situados paralelamente, tomas el de la izquierda A, lo desplazas hasta una altura H y lo sueltas colisionando con B, el del extremo contrario F se eleva hasta una altura H'. Este experimento ya fue realizado y estudiado por Mariotte a mediados del siglo XVIII. Si H' = H , es necesario que :

a) TODAS LAS MASAS SEAN IGUALES

b) TODAS LAS COLISIONES DEBEN SER ELÁSTICAS

c) LOS CENTROS DE LAS ESFERAS TIENE QUE ESTAR ALINEADOS

d) NO DEBE PRODUCIRSE RUIDO EN LA COLISIÓN

e) TODAS LAS ESFERAS DEBEN ESTAR EN CONTACTO

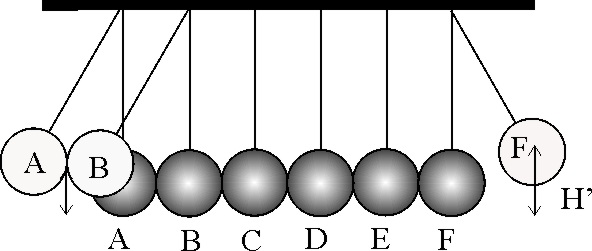
3.5.15.Si en el experimento anterior, con 6 péndulos iguales, tomas las esferas A y B, las elevas hasta una altura H, y las sueltas colisionando elásticamente con C:

a) LA F SE ELEVA HASTA UNA ALTURA H’= 2H

b) LA F SE ELEVA DE FORMA QUE EL ÁNGULO DE SEPARACION SEA DOBLE DEL QUE SERÍA SI SÓLO COLISIONASE A

c) ASCIENDEN LAS ESFERAS E Y F HASTA UNA ALTURA H’=H

d) NO OCURRE NADA PUES SE COMPENSAN LAS COLISIONES

e) A, SE ELEVA POR LA IZQUIERDA Y F, POR LA DERECHA HASTA UNA ALTURA H’=H

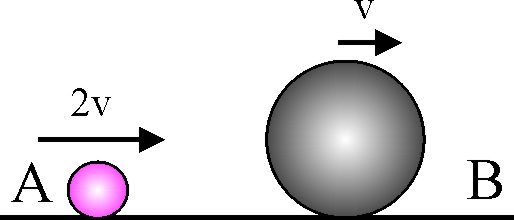
3.5.16.En una mesa de billar, sin rozamiento y suponiendo una rotación nula, se lanza una bola blanca B con una velocidad v, sobre otra negra N de la misma y en reposo. Después de la colisión frontal y perfectamente elástica, podrás asegurar que las velocidades de las bolas blanca y negra después de la colisión son respectivamente:

a) 0 y v b) v y 0 c/ v/2 y v/2 d) v y v

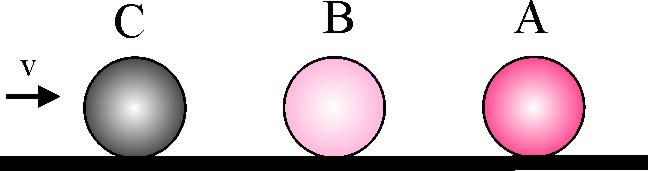
3.5.17.En una mesa de billar se encuentran 3 bolas de masas iguales, A, B y C. Inicialmente dos bolas A y B, están en reposo y separadas. Se lanza con una velocidad de módulo v, una tercera bola C, alineada con A y B, de forma que choque elásticamente primero con B y después ésta con A. Si se desprecian los posibles rozamientos con el fieltro de la mesa, y la rotación de las bolas, podrás asegurar que después de las colisiones:

a) EL MÓDULO DE LA VELOCIDAD DE LAS 3 BOLAS ES EL MISMO

b) LAS BOLAS C Y B SE DETIENEN Y SÓLO SE MUEVE A, CON VELOCIDAD .

c) B SE DETIENE, A SE MUEVE CON VELOCIDAD Y C REBOTA CON UNA VELOCIDAD -

d) B SE DETIENE, A SE MUEVE CON VELOCIDAD /2 Y C REBOTA CON VELOCIDAD - /2

e) LAS TRES ESFERAS SE DESPLAZAN CON UNA VELOCIDAD /3

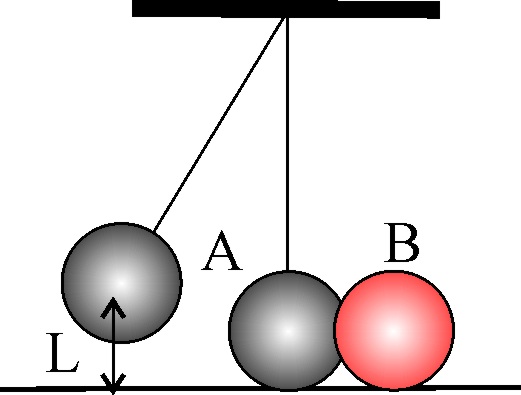
3.5.18*.El bloque de la figura A actúa como un péndulo desde su posición golpeando inelásticamente a B de su misma masa y con rozamiento despreciable con el suelo, al soltarlo desde una altura L. Si estudias detalladamente dicha colisión y supuesta la masa de A, M, podrás decir que:

a) LA VELOCIDAD CON QUE SALEN A Y B DESPUÉS DEL CHOQUE ES EN m/s

b) LA ENERGÍA PERDIDA EN LA COLISIÓN ES MgL/2 J.

c) LA ALTURA ALCANZADA POR EL CONJUNTO AB ES L/4

d) EL ÁNGULO DE MÁXIMA DESVIACIÓN DEL NUEVO PÉNDULO ES DE

e) LA TENSIÓN DE LA CUERDA EN EL PUNTO MÁS BAJO DE LA TRAYECTORIA ES DE 5Mg/2 N

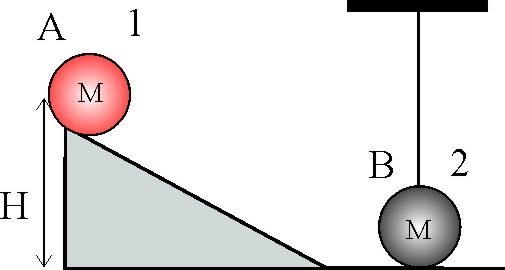
3.5.19.Si se abandona cierto cuerpo A de masa M, desde la posición 1 a una altura H, chocando inelásticamente en la posición 2 con el cuerpo B de la misma masa, suspendido sin rozamiento de un hilo y el sistema se eleva hasta una altura H/8, podrás afirmar que la energía perdida por A desde 1 hasta que choca será en julios :

a) MgH/2 b) MgH c) MgH/4 d) MgH/8

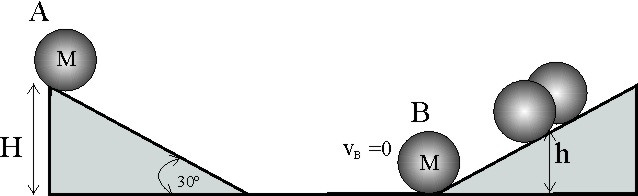
3.5.20.En el sistema de la figura se deja deslizar el cuerpo A de masa M desde lo alto de un plano inclinado y altura H con coeficiente de rozamiento =0,1. Al final del plano horizontal, de igual longitud que los inclinados se encuentra con B de igual masa e idéntico coeficiente de rozamiento, con el que choca quedando adosado, de forma que ambos ascienden juntos por el otro plano inclinado hasta una altura h, en metros igual a :

a) 0,13H b) 0,15H c) 0,20H d) 0,5H

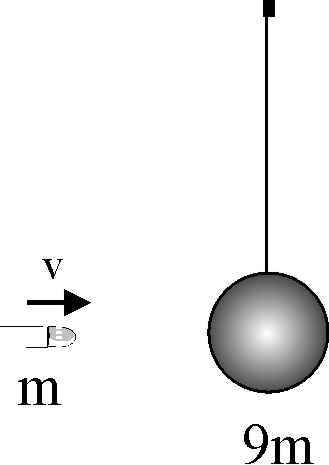
3.5.21. El péndulo balístico fue inventado por el matemático e ingeniero militar inglés Robins, a mediados del siglo XVIII, para determinar la velocidad de las balas y el poder explosivo de la pólvora. Si en un péndulo balístico, la bala de masa m, se incrusta frontalmente en una masa 9m, suspendida de un hilo de longitud L, de forma que ambos alcanzan su máxima altura, sin caer podrás afirmar que la mínima velocidad , con que incidió la bala en el péndulo, deberá ser, en m/s:

b) 10 /9

c) 20

d) 10

3.5.22. Si un cuerpo A de masa m, con una velocidad determinada colisiona frontalmente con otra B de masa 9m, en reposo, suspendida de un hilo inelástico de forma que a consecuencia del choque , la pendular adquiere la máxima altura sin caerse, la relación entre las velocidades que deberá llevar A para ello según sea la colisión completamente elástica, o inelástica valdrá:

a) b) 2 c) 0,5 d)

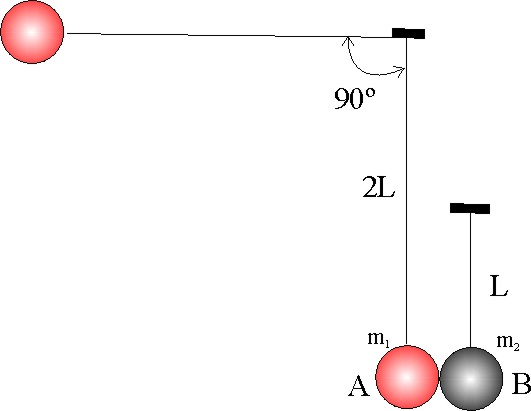
3.5.23.Dispuestas dos esferas A y B de masas respectivas m₁ y m₂, en dos péndulos paralelos de longitudes respectivas, 2L y L. Si al separar A, hasta formar un ángulo de 90 grados, y soltarla colisiona frontal y elásticamente con B, de tal forma que después de la colisión su hilo pendular forma un ángulo de con su posición vertical, dirás que la relación de las masas de A y B es aproximadamente:

a) 1/2 b) 2 c) 1+ d) 1/

mientras que si B alcanza su máxima altura sin caerse, dicha relación sería aproximadamente:

a) 1,5 b) 2,25 c) 1,27 d) 2,5

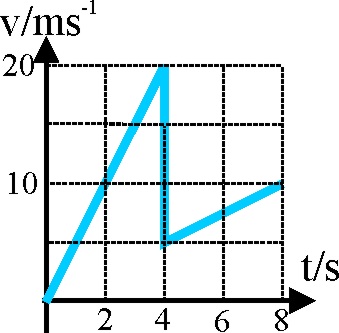
3.5.24*.Una locomotora de tren de masa M, que circula con una determinada aceleración por la vía, colisiona con otro de masa desconocida m, que se encuentra parado en la vía circulando los dos conjuntamente, según una gráfica v/t que representa las variaciones de v, con el tiempo a lo largo de la colisión. Si examinas detenidamente dicha gráfica, podrás asegurar que :

a) LA COLISIÓN OCURRIÓ A LOS 4s DE COMENZAR A CONTAR LOS TIEMPOS

b) LA ACELERACIÓN DE LA LOCOMOTORA ES DE 5m/s²

c) LA MASA DEL VAGÓN PARADO ES LA TERCERA PARTE DE LA DE LA LOCOMOTORA

d) LA ENERGÍA PERDIDA EN LA COLISIÓN ES DE 150M J

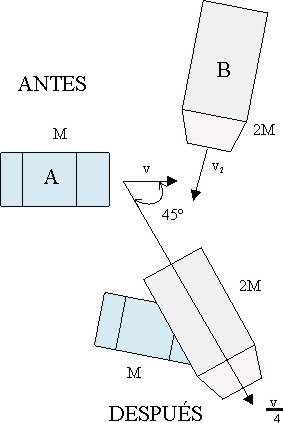
3.5.25.Dos vehículos A y B, de masas respectivas M y 2M colisionan inelásticamente. Su velocidad después del impacto tiene de módulo, la cuarta parte del de la velocidad inicial del más ligero v, con cuyo vector forma un ángulo de . Podrás decir por lo tanto que el módulo de la velocidad del más pesado antes del choque era :

a) 0,5v b) 0,35v c) 0,45v d) LA CUARTA PARTE

Mientras que el ángulo que forma las velocidades de A y B será de

a) b)

c) d)

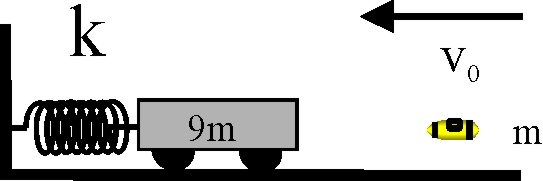
3.5.26. Si se dispara un proyectil de masa m con velocidad inicial , de forma que quede empotrado en M, de masa 9m, sujeto en el extremo de un resorte de coeficiente elástico k, dirás que la máxima deformación de dicho resorte x, será de :

a) b) v₀

c) d)