ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
1.8. MOVIMIENTO RELATIVO
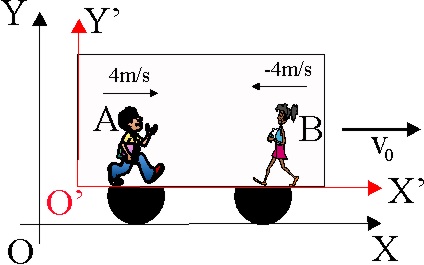
1.8.1. Dos
niños A y B, se mueven dentro de un vagón de tren, que circula con una velocidad
v0 =4 m/s, y en el sentido indicado, con velocidades respecto al tren, de módulo igual a 4 m/s y en los sentidos indicados. Dirás que las velocidades
de A y B, respecto a los raíles serán, en m/s, respectivamente:
a) 4 Y 4
b) 8 Y 4 c) 8 Y 0
d) 0 Y 8
e) NADA DE LO DICHO
a) SUR Y SURESTE
b) NORTE Y NOROESTE
c) NORTE Y NORTE
d) OESTE Y SUROESTE
e) NADA DE LO DICHO
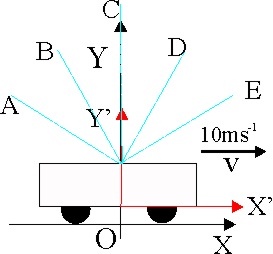
1.8.3. Un
viajero va sentado en un vagón de carga que se mueve en el sentido indicado
a 10 m/s. Empieza a llover, sin viento, y las gotas caen con una velocidad,
cuyo módulo vale 5 m/s. El esquema de todos los dados que se ajustaría a como
vería caer las gotas de la lluvia, sería el:
a)
A b) B c) C d)
D
e)
E f) NINGUNO
1.8.4*. Se
quiere llegar en una hora de vuelo, a una ciudad que dista 1000km, hacia el
oeste, del aeropuerto. El viento sopla del sur, a la altura de vuelo del avión,
a 200 km/h. Por lo tanto, el comandante
de la nave, situándola en el origen de coordenadas, de unos hipotéticos ejes
X/Y, debe llevar una velocidad, en km/h, de:
a) -1000i+200j
b) -1000i-200j
c) 1000i+200j
d) QUE EN km/h TIENE
POR MÓDULO
e) NADA DE LO DICHO
1.8.5. Si
una partícula A se mueve en relación a otra B con una velocidad relativa de
2i+3j m/s, y B se mueve en relación a C a i+2j
m/s, la velocidad de A respecto a C, será en m/s:
a) i-j
b) 3i+5j
c) TIENE POR MÓDULO 5
d) -i-j
e) NADA DE LO DICHO
1.8.6. Si
la hoja de un árbol se mueve con relación a un observador fijo en tierra con
una velocidad de 6i+2j m/s, y pasa un coche con una velocidad
respecto a ese observador de 2i-j m/s, la velocidad de la hoja
respecto a una persona que va dentro del vehículo tendrá por módulo en m/s:
a)
b) 5 c)
d)
e) NINGUNO DE LOS DADOS
1.8.7. Un
nadador pretende atravesar un río de L=24m de ancho desde una orilla a la
otra. Si la velocidad de la corriente en el sentido indicado es 0,6m/s y la
máxima velocidad que puede desarrollar es de 1m/s, tardará en llegar a la
otra orilla, como mínimo, en segundos:
a) 30
b) 300 c) 24 d) 20,3
e) NADA DE
LO DICHO
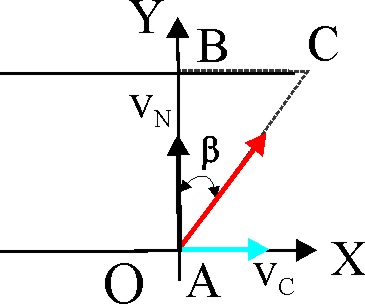
1.8.8. Un
barquero quiere llegar remando de A a B, según el esquema de la figura, que
distan entre sí 200m, en 10 minutos. Pero la corriente lleva una velocidad
de 3ikm/h, por eso deberá llevar una velocidad, respecto a un sistema
de ejes centrado en A, en km/h de:
a) -3i+1,2j
b) 3i+1,2j
c) 3i-1,2j
d) -3i-1,2j
e) NADA DE LO DICHO
Pero si no
tuviera en cuenta la orientación debida y remara con la misma velocidad que
en el caso anterior en dirección a B, lo que ocurriría es que aparecería río
abajo a una distancia de B en metros, de:
a) 200
b) 187 c) 100
d) 280
e) NINGUNO DE LOS VALORES DADOS
1.8.9.* La
velocidad de la corriente de un río no suele ser constante, siendo máxima
VM en su centro y nula en las orillas, si un bote se mueve desde
la orilla con velocidad v perpendicular a la corriente con el objeto de
llegar a la orilla opuesta separadas una distancia d, podrás asegurar que:
a) SU TRAYECTORIA ES UNA PARÁBOLA
b) EL CAMINO QUE SIGUE ES UNA RECTA INCLINADA RESPECTO
A LA OTRA ORILLA
c) LA LEY DE LA VELOCIDAD DE LA CORRIENTE ES V=(2VM/d)x, SIENDO x LA DISTANCIA MÍNIMA RECORRIDA
d) LA DISTANCIA RECORRIDA EN LA ORILLA OPUESTA RESPECTO
A SU PUNTO DE PARTIDA, SERÁ VMd/2v.
1.8.10. La
noche de fin de año se celebra con un baile-cena en un barco que navega
río arriba. Uno de los pasajeros con ánimo de despejarse la borrachera,
o a consecuencia de ella, se tira (con un salvavidas) al agua. A las voces
de ¡Hombre al agua!, el barco da la vuelta para recoger al náufrago, tardando
en la operación de cambio de sentido, desde que se arrojó al agua, minuto
y medio, volviendo con igual velocidad para el rescate, que realiza a 900
metros del punto donde cayó. Con estos datos podrás asegurar que la corriente
llevaba una velocidad en m/s de:
a) 5
b) 18 c) 15
d) 10
e) NINGUNO DE LOS VALORES DADOS
1.8.11.* Si
la ciudad B, dista 4000 km hacia el oeste de la A, y el comandante piloto
del avión, pretende tardar 5 horas en el vuelo desde A hacia B, con el viento
soplando del sudeste a 100km/h, y el mismo tiempo en el viaje de vuelta
(sin que varíe ni la dirección ni la fuerza del viento), dirás que para
todo ello, deberá:
a) LLEVAR UNA VELOCIDAD RESPECTO AL VIENTO, CUANDO
VA DE A HACIA B, CON MÓDULO DE 733 km/h
b) SEGUIR UN RUMBO HACIA B, CON ÁNGULO DE APROXIMADO
DE
DE DESVIACIÓN SOBRE
LA RECTA DE UNIÓN DE AMBAS CIUDADES
c) NO MODIFICAR EL MÓDULO DE SU VELOCIDAD EN EL
VIAJE DE VUELTA
d) ALTERAR EL RUMBO EN EL RETORNO, HASTA FORMAR
UN ÁNGULO DE
CON LA RECTA QUE UNE B Y A
e) NADA DE LO DICHO
1.8.12. En
una excursión veraniega en barco, observas que cuando el barco se mueve
hacia el sudeste, si sacas un pañuelo y lo dejas ondear, lo hace hacia el
este. Sin embargo, sin haber cambiado la orientación, ni del barco ni del
viento, cuando aquel reduce su velocidad hasta la mitad, el pañuelo ondea
ahora hacia el nordeste. De estos hechos puedes deducir que el viento sopla:
a)
DEL NOROESTE b) DEL NORTE
c)
DEL SUR
d) DEL SUDESTE
e)
FORMANDO UN ÁNGULO DE
CON EL NORTE
1.8.13. De
vez en cuando, al ir al cole, te pilla un buen chaparrón, pero como eres
bastante previsor, abres un paraguas plegable, y lo dispones con una inclinación
respecto al suelo de
, y caminas rápidamente a 5 km/h(respecto al suelo).
En tu camino te das cuenta que sólo faltan 5 minutos para la hora de entrada,
y duplicas tu velocidad. Pues bien, el ángulo que deberá formar tu paraguas
con el suelo para no mojarte deberá ser aproximadamente de:
a)
b)
c)
d)
e) NADA DE LO DICHO
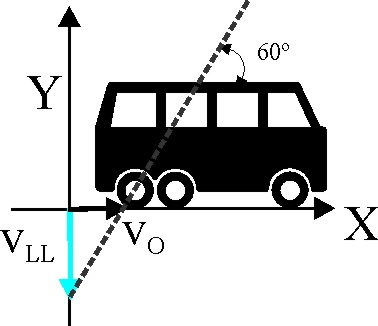
1.8.14. Con
bastante frecuencia cuando vas en autobús, habrás observado que las gotas
de lluvia caen sobre los cristales formando un determinado ángulo, aunque
no haga viento. Si la velocidad de la lluvia es de 30m/s, en relación al suelo,
y el ángulo que observas es de aproximadamente
con la horizontal, como indica el dibujo,
podrás asegurar que el autobús marchaba a una velocidad aproximada, en km/h
de:
a) 90 b)
60 c) 30
d) 100 e) NINGUNO DE LOS VALORES DADOS
1.8.15. Fácilmente
puedes realizar un experimento casero de movimiento relativo. Tomas una hormiga,
y la sitúas en un punto medio de un disco que gira a 33 rpm. Si la hormiga
avanza en línea recta hacia el centro del disco, la trayectoria que observarías
sería:
a) UNA CIRCUNFERENCIA
b) CIRCUNFERENCIAS
CONCÉNTRICAS
c) UNA ESPIRAL
d) UNA PARÁBOLA
e) NADA DE
LO DICHO
1.8.16.* Si
en un ascensor que sube con una velocidad constante de 1 m/s, a dos metros
de su suelo, vuela una polilla, alrededor de la lámpara, describiendo circunferencias
de radio 0,2 m, con velocidad angular constante de 0,2 rad/s, para un observador
situado en reposo, fuera del asensor y en su vertical:
a) LA POLILLA DESCRIBIRÍA UNA RECTA
b) LA ECUACIÓN DEL MOVIMIENTO DE LA POLILLA SERÍA
x=0,2·cos(0,2t) ,
y=0,2·sen(0,2t) , z=2+t
c) LA ACELERACIÓN DEL MOVIMIENTO SERIA 0
Mientras que para una araña situada en el
suelo del ascensor:
a) LA POLILLA DESCRIBIRÍA UNA TRAYECTORIA RECTA
b) LA ECUACIÓN DE SU MOVIMIENTO SERÍA z=2
c) LA ACELERACIÓN DE SU MOVIMIENTO SERÍA LA MISMA
QUE PARA EL OBSERVADOR SITUADO EN REPOSO FUERA DEL ASCENSOR
1.8.17.* Un
muchacho aprovecha el viaje en ascensor, en solitario, hasta el piso donde
vive, para jugar a las canicas, golpeando una de ellas, que rueda por su suelo
con velocidad constante de 50i cm/s, si el ascensor asciende a partir
del reposo con una aceleración constante de 2j m/s2, dirás
que para un observador situado en reposo fuera del ascensor:
a)
LA TRAYECTORIA DE LA CANICA ES RECTILÍNEA
b)
LA ACELERACIÓN NORMAL AL CABO DE 0,25 s ES DE
m/s2
c)
EL RADIO DE CURVATURA AL CABO DE 0,25 s ES DE 0,35 m
Mientras que para el muchacho:
a)
EL MOVIMIENTO DE LA CANICA ES RECTILÍNEO Y UNIFORMEMENTE ACELERADO
b)
AL CABO DE 0,25s SE SEPARÓ DE
SU DEDO 12,5 cm
c)
LA TRAYECTORIA DE LA CANICA TIENE POR ECUACIÓN y=0,1x
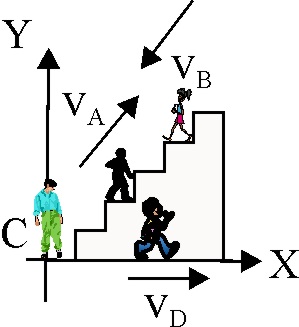
1.8.18. En
una escalera rodante de unos grandes almacenes, un comprador A, asciende a
una velocidad de i+j m/s, mientras que otro B, desciende en
sentido contrario. En el piso inferior, hay
dos espectadores, uno en reposo, C y otro, D desplazándose con velocidad
de i m/s. Cuando A y B, se cruzan, la velocidad:
a) DE A RESPECTO A B SERÁ 0
b) DE B RESPECTO A D TENDRÁ POR MÓDULO
m/s
c) DE C RESPECTO A A SERÁ -2j m/s
d) DE B RESPECTO A A TENDRÁ POR MÓDULO
m/s
1.8.19. En
un ascensor transparente viaja Pedro D, que sostiene a un metro del suelo
del ascensor, un regalo para obsequiar a su madre. Ese ascensor sube con una
velocidad de régimen constante de 2m/s. Al mismo nivel por las escaleras,
los vecinos A y B, suben y bajan respectivamente con una velocidad de 1m/s,
con la misma que C se desplaza por dicha planta de izquierda a derecha, mientras
que E, observa a todos, de pie y en reposo. En ese momento, se le cae el regalo
a D. El módulo de la velocidad con que llega al suelo, será diferente según
cada observador, y el orden de estos, de mayor a menor será:
a) A>B>C>D>E b) D>A>C>E>B
c) D>B>C>E>A
d) D>A>B>C>E
e) B>D>A>E>C f) A>D>B>C>E
1.8.20.*
En
una excursión en un barco que zarpa perpendicularmente al muelle, con velocidad
v, uno de los pasajeros que estaba asomado en estribor (borda derecha),
se mueve rápidamente, aunque a velocidad constante V, a babor, perseguido
por una avispa que da vueltas a su alrededor con un radio de 0,5m, y con velocidad
angular constante,
. Para el observador en el muelle, supuesto en un origen de coordenadas, el
movimiento de la avispa:
a)
TENDRÁ UNA TRAYECTORIA ESPIRAL INCLINADA
b)
SERÁ UNIFORMEMENTE ACELERADO
c)
SERÁ UNIFORME PORQUE NO HAY ACELERACIÓN
d)
TENDRÁ UNA ECUACIÓN:
r=(vt+0,5·sen
t)i+(Vt+0,5·cos
t)j m
e)TENDRÁ UNA ECUACIÓN:
r=(Vt+0,5·cos
1.8.21.* Aunque
está a la vista el cartel que prohibe arrojar objetos por la ventanilla de
un tren, cierto "gamberrete", pretende alcanzar un poste del tendido
eléctrico con un botellín de cerveza, lanzándola al pasar a su altura desde
la ventanilla a 2,5m del suelo, perpendicularmente hacia afuera, con una velocidad
de 5m/s. El poste se encuentra en ese momento a 4m de la vía y el tren iba
a 108 km/h. Es evidente que ni tiene educación, ni sabe física, porque:
a) EL VECTOR DE POSICIÓN DEL GAMBERRO RESPECTO A
UN SISTEMA DE EJES CENTRADO EN EL POSTE, ES 30ti-4j+2,5k
m
b) EL VECTOR DE POSICIÓN DEL OBJETO RESPECTO A UN
SISTEMA DE EJES CENTRADO EN EL TREN, ES 5tj-5tk m
c) EL VECTOR DE POSICIÓN DEL OBJETO AL LLEGAR AL
SUELO, RESPECTO AL SISTEMA DE EJES TOMADO COMO FIJO (POSTE), ES APROXIMADAMENTE
DE 21i-0,5j m
1.8.22. Un
punto material se mueve respecto a un sistema de ejes móviles O', con un vector
de posición, r'=(4t2-7t-2)i+2j+4k
m, mientras que lo hace
respecto a un sistema fijo O, con r=(4t2+2t+3)i-2j+3k
m, por todo ello dirás
que:
a) EL PUNTO LLEVA UN MOVIMIENTO UNIFORMEMENTE ACELERADO
RESPECTO A AMBOS EJES
b) EL EJE MÓVIL SE ACERCA AL EJE FIJO A VELOCIDAD
CONSTANTE
c) EL EJE MÓVIL SE ALEJA DEL EJE FIJO CON UN MUA
d) LA VELOCIDAD DE ARRASTRE ES -9i ms-1
e) LA ACELERACIÓN DE ARRASTRE ES 0
1.8.23.* Las
ecuaciones paramétricas de un punto material respecto a un eje fijo son x=t3-t+1,
y=3t3+1, z=4t4-2, sin embargo respecto de un eje móvil
O', son x'=t3-3t+5, y'=2+3t3, z'=3+4t4, en
función de ello podrás asegurar que:
a)
O' SE MUEVE RESPECTO A O, CON UN MOVIMIENTO VARIADO
b)
LA VELOCIDAD DE ARRASTRE TIENE POR MÓDULO 2
c)
LA ACELERACIÓN DE ARRASTRE VALE 0
d)
EL PUNTO MATERIAL SE MUEVE CON UN MOVIMIENTO VARIADO
e) O' SE MUEVE PARALELAMENTE A O
1.8.24. Un
punto material se desplaza respecto a ejes fijos O, con un vector de posición
r=t3i+(2+t2)j-(t+1)k m, mientras que lo hace en un sistema
de ejes móviles O', con r'=t3i-(2t2-2)j+4k
m, por todo ello podrás
decir que el sistema de ejes móviles, se desplaza respecto a O:
a)
CON VELOCIDAD CONSTANTE
b)
CON ACELERACIÓN CONSTANTE
c)
CON UN MOVIMIENTO RECTILINEO
d)
CON ACELERACIÓN DE ARRASTRE 6k m/s2
e)
CON UN MOVIMIENTO RETARDADO
1.8.25.** Sobre un vehículo de carga y a 1,5m de su extremo y 2m
de la vertical del suelo, se apoya un fardo de 2 kg que tiene un coeficiente
de rozamiento con la superficie de la caja del camión de 1/5. El vehículo
arranca con una aceleración de 5 m/s2, que mantiene durante 2 segundos.
Este hecho va a producir una serie de fenómenos tales como:
a) EL FARDO CAE DE LA CAJA AL SEGUNDO DE ARRANCAR
b) LA VELOCIDAD CON QUE SALE DE LA CAJA RESPECTO
AL SUELO ES DE 3 m/s
c) LA VELOCIDAD CON QUE SALE DE LA CAJA RESPECTO
AL CONDUCTOR ES DE 8 m/s
d) EL FARDO CAE AL SUELO A 2,5m DEL PUNTO DE SALIDA
DEL CAMIÓN
e) LA TRAYECTORIA DE CAÍDA DEL FARDO RESPECTO A
UN OBSERVADOR FIJO EN EL PUNTO DE SALIDA SERÁ UNA RECTA
tómese g como 10ms-2
1.8.26.* Un
helicóptero que inicialmente se encuentra parado a una altura h, de una planicie
montañosa, realiza una operación rescate de un montañero, que es izado por
una cuerda con una aceleración de 2j m/s2, respecto a un
observador inercial que se encuentra en la montaña, al mismo tiempo que avanza
hacia su frente alejándose de la montaña, con una aceleración de 2i
m/s2. De todo ello dirás que:
a) PARA UN OBSERVADOR INERCIAL, EL ÁNGULO QUE FORMA
LA CUERDA CON EL HELICÓPTERO ES DE
b) UN OBSERVADOR QUE VIERA EL RESCATE DESDE LA MONTAÑA
APRECIARÍA QUE LA TRAYECTORIA DEL MONTAÑERO SERÍA UNA RECTA DE ECUACIÓN x=y
c) EL MONTAÑERO RESCATADO OBSERVARÍA QUE EL HELICÓPTERO
SE ACERCA A ÉL CON UNA ACELERACIÓN DE -2j ms-2
d) EL PILOTO DEL HELICÓPTERO OBSERVARÍA QUE EL MONTAÑERO
SE LE ACERCA, CON UNA ACELERACIÓN DE MÓDULO
ms-2
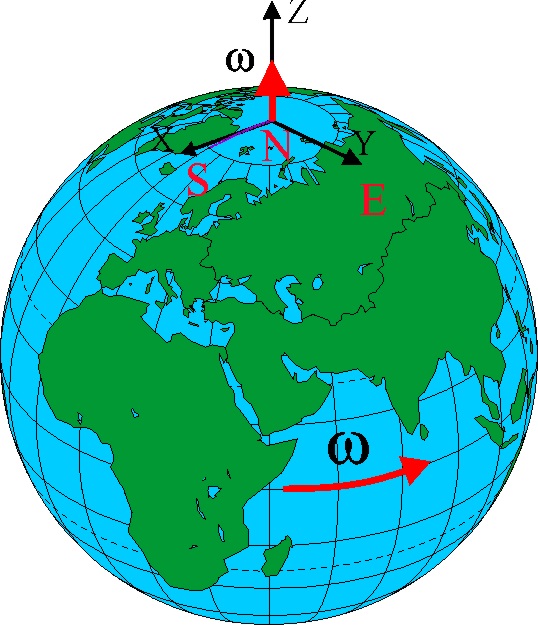
1.8.27.* Si
un iceberg que se desprende del casquete polar ártico, se desplaza hacia el
sur siguiendo aproximadamente un meridiano (como se indica en el dibujo),
con una velocidad de 12 km/h sufrirá una desviación en su movimiento:
a) QUE
SERÁ DEBIDA AL GIRO DE LA TIERRA Y A LA FUERZA CENTRÍFUGA
b) QUE
SE PRODUCIRÁ POR EL GIRO DE LA TIERRA Y LA FUERZA DE CORIOLIS
c) QUE
LO DESPLAZARÁ HACIA EL SUR
d) QUE
LO DESVIARÁ HACIA EL OESTE
e) EN CADA HORA DE
km
1.8.28.* Cuando
observas la información del tiempo por televisión, sueles apreciar en las
imágenes del satélite Meteosat, manchas de nubes en forma de espiral en un
régimen de bajas presiones, orientadas en un sentido determinado. Este hecho
viene determinado por la fuerza de Coriolis, que en este caso y en el hemisferio
norte desviaría las nubes:
a)
HACIA EL NORTE
b)
EN SENTIDO HORARIO
c)
HACIA EL ESTE
d)
HACIA EL SUR
e)
EN SENTIDO ANTIHORARIO
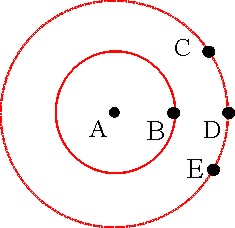
1.8.29.* En
un carrusel de feria, esquematizado en el dibujo, el encargado, situado en
la posición A, junto al eje del tiovivo, que gira con velocidad angular constante,
lanza un balón que se había dejado olvidado en uno de los coches, un chico
D, que se encuentra observando como su amigo B, gira montado en un caballito.
Con tus conocimientos de física podrás asegurar que :
a) B VERÁ PASAR EL BALÓN POR DELANTE DE SUS
NARICES
b) EL BALÓN LLEGARÁ A E
c) C RECIBIRÁ EL BALON
d) EL BALÓN PASARÁ POR DETRÁS DE B
e) EL BALÓN LLEGARÁ SIN DESVIARSE A D
