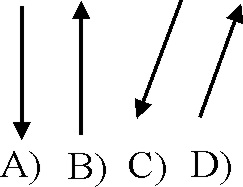ENSEÑANZA
DE LA FÍSICA Y LA QUÍMICA
1.4.1. Si
un cuerpo es lanzado verticalmente hacia arriba con velocidad inicial V0,
llegando hasta una altura H, al duplicar su velocidad inicial, el tiempo que
tardaría ahora en llegar a H, sería:
a)
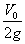 b)
b)
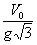 c)
c)
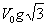
d)
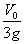 e) NADA DE LO DICHO
e) NADA DE LO DICHO
1.4.2. Un
cuerpo lanzado verticalmente hacia arriba con velocidad inicial V0,
llega a la mitad de su trayectoria ascendente, una vez transcurrido un tiempo
en segundos de:
a)
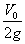 b)
b)
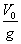 c)
c)
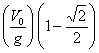
d) LA MITAD DEL TIEMPO TOTAL e) NADA DE LO DICHO
1.4.3. Si
dejas caer una esfera metálica desde una altura H y después de rebotar en
el suelo alcanza una altura H/2, la
relación entre los módulos de sus velocidades antes y después de llegar al
suelo, será de:
a) 2
b)
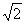 c)
c)
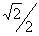
d)
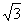 e) NADA DE LO DICHO
e) NADA DE LO DICHO
1.4.4.* Si
lanzas verticalmente hacia arriba un móvil con una velocidad inicial de 40
m/s, al cabo de 7s podrás afirmar que:
a) SUS VECTORES VELOCIDAD Y ACELERACIÓN CAMBIARON
DE SENTIDO
b) EL MÓVIL SUBE CON UNA VELOCIDAD DE 30 m/s
c) EL MÓVIL BAJA CON UNA VELOCIDAD DE 30 m/s
d) SU VECTOR ACELERACIÓN CAMBIÓ DE SENTIDO, NO ASÍ
SU VELOCIDAD
e) SU VECTOR VELOCIDAD CAMBIÓ DE SENTIDO, NO ASÍ
SU ACELERACIÓN
1.4.5. Desde
determinada altura H, se deja caer un cuerpo desde el reposo y simultáneamente
se lanza hacia arriba, con una velocidad incial V0, un cuerpo 10
veces mayor que el primero. Suponiendo que no existe rozamiento, el tiempo
que tardan en encontrarse será en segundos de:
a) H/2V0 b) 10H/V0
c) H/V0
d)
H/10V0 e) NADA DE LO DICHO
1.4.6. Si
una esfera que se mueve por una mesa de altura H, con una velocidad V0,
cae al suelo a una distancia X de la vertical de la mesa, la relación entre
H y X será:
a)
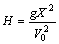 b)
b)
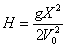 c)
c)
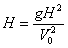
d)
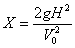 e) NINGUNA
DE LAS DADAS
e) NINGUNA
DE LAS DADAS
1.4.7. Si
calculas la velocidad inicial con que rueda por una mesa de altura H, sobre
el suelo, una esfera que al caer desde aquella al mismo, lo alcanza a una
distancia de la vertical de la mesa igual a H, dirás que valdrá en m/s:
a)
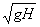 b)
b)
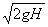 c)
c)
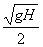
d)
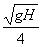 e) NADA DE LO DICHO
e) NADA DE LO DICHO
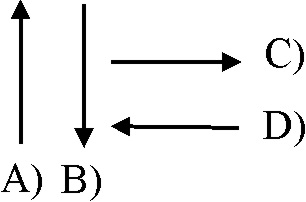
1.4.8. Si
una esfera que rueda por una mesa con una determinada velocidad, cae al suelo,
la gráfica de la variación de su velocidad horizontal con el tiempo será de
todas las dadas, la:
a) A b) B c) C
d) D e) NINGUNA
1.4.9. Los
gráficos dados corresponden al estudio del movimiento de caída de un cuerpo
lanzado horizontalmente desde una altura H en el campo gravitatorio terrestre,
en un referencial situado en el suelo y sin tener en cuenta el rozamiento.
Deberás relacionar
cada gráfico representado por una letra, con la variación de una determinada
magnitud de su movimiento:
A
1) x/t
B
2) y/t
C 3) vx/t
D
4) vy/t
E
5) x/y
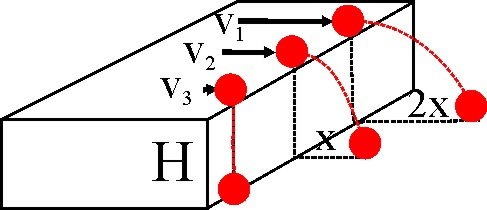
1.4.10.* En
el dibujo de la figura puedes observar 3 esferas iguales que caen desde la
misma altura, impulsadas por velocidades diferentes, llegando al suelo al
cabo de unos tiempos respectivos t1, t2 y t3,
y a unas distancias 2X, X y 0. De aquellas podrás afirmar que:
a) V1=2V2>V3 b) V1>2V2>V3
c) V1<2V2>V3
d)
t1>t2>t3
e) t1=t2=t3
1.4.11. Los
gráficos dados corresponden al movimiento de un cuerpo lanzado oblicuamente
desde el suelo y hacia arriba en el campo gravitatorio terreste, en un referencial
situado en el suelo y sin rozamiento.
Deberás relacionar
cada gráfico representado por una letra, con la variación de la magnitud
dada, que le corresponda:
a)
A b) B c) C d)D e) E
1)
x/t
2) y/t
3) vx/t
4) vy/t 5)
x/y
1.4.12. Si
se lanza un proyectil con un determinado ángulo y velocidad inicial, el vector
de los dados que mejor representa la velocidad de dicho proyectil en el punto
más alto de su trayectoria, es el:
a) A
b) B c) C
d) D
e) NINGUNO
DE LOS DADOS
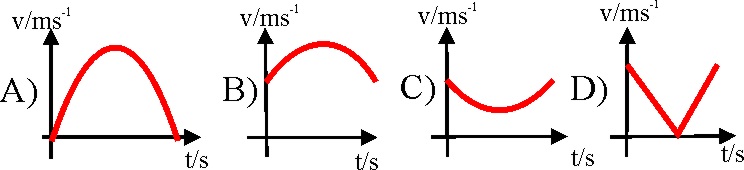
1.4.13. Cuando
se lanza un proyectil con un determinado ángulo y velocidad inicial, en el
campo gravitatorio terrestre, sin considerar el rozamiento, la gráfica módulo de v respecto a t que mejor representa
la variación de su velocidad, de todas las dadas, será la:
a) A
b) B c) C
d) D
e) NINGUNA
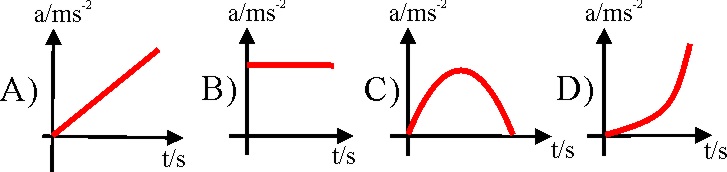
Y la que mejor
representa la variación de su aceleración, de todas las dadas será la:
a)
A b) B
c) C
d)
D e) NINGUNA
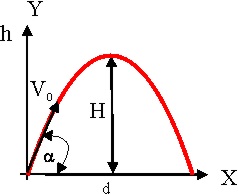
1.4.14. Si un proyectil lanzado con una
determinada velocidad inicial V0,
y un ángulo
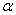 , con la horizontal, después de alcanzar una altura máxima H, llega al suelo
a una distancia d del punto de lanzamiento, podrás decir que:
, con la horizontal, después de alcanzar una altura máxima H, llega al suelo
a una distancia d del punto de lanzamiento, podrás decir que:
a) d AUMENTA A MEDIDA QUE LO HACE
b) A LA ALTURA H
,
c) A LA ALTURA H,
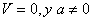
d) EN d,
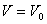
e) EN H,
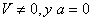
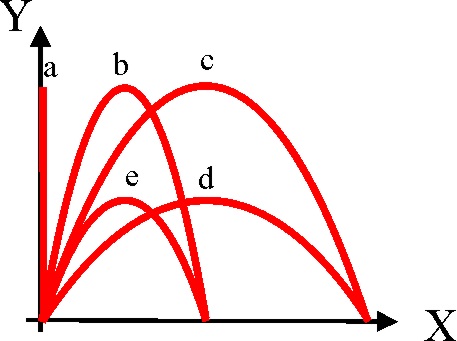
1.4.16. Examinando las trayectorias de cinco
objetos iguales lanzados hacia arriba en el mismo plano vertical y sin rozamiento,
podrás decir que la que corresponde al móvil lanzado con un módulo de su velocidad
inicial mayor, será la:
a) A
b) B
c) C
d) D
e) E
DATO: Aproximadamente los
ángulos de lanzamiento son :
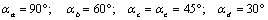
1.4.17. Si se lanza un proyectil con una
determinada velocidad inicial formando un determinado ángulo de
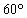 con la horizontal, y despreciando la
resistencia del aire, el vector que mejor nos da la diferencia entre el vector
velocidad en el punto mas alto de su trayectoria y la velocidad en el instante
de lanzamiento, es de todos los dados el:
con la horizontal, y despreciando la
resistencia del aire, el vector que mejor nos da la diferencia entre el vector
velocidad en el punto mas alto de su trayectoria y la velocidad en el instante
de lanzamiento, es de todos los dados el:
a) a
b) b c) c d) d
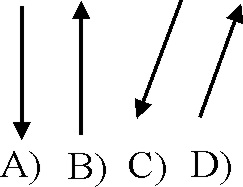
1.4.18. Cuando lanzas un proyectil oblicuamente
formando un ángulo
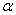 con la horizontal y con velocidad inicial
V0, éste deberá llegar al suelo supuesto en la misma horizontal,
en un punto que tendrá por coordenadas (X,Y), referidas
al punto de lanzamiento como origen:
con la horizontal y con velocidad inicial
V0, éste deberá llegar al suelo supuesto en la misma horizontal,
en un punto que tendrá por coordenadas (X,Y), referidas
al punto de lanzamiento como origen:
a)
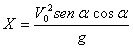 ,Y=0
,Y=0
b)
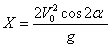 ,Y=0
,Y=0
c)
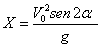 ,Y=0
,Y=0
d)
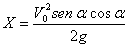 ,Y=0
,Y=0
e) NADA
DE LO DICHO
1.4.18.1. Siendo el valor de
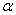 en grados para que su altura fuera
máxima:
en grados para que su altura fuera
máxima:
a) 30
b) 45 c) 60 d) 90
e) NADA DE LO DICHO
1.4.18.2. Y para que su alcance fuera máximo:
a) 30
b) 45 c) 60 d) 90
e) NADA DE LO DICHO
1.4.19. Si un avión que vuela a 2000 m de
altura y con una velocidad constante en su vuelo horizontal de 300 m/s, lanza
una bomba, podrán oir la explosión de dicha bomba desde el avión, en un lugar
que dista de la posición de lanzamiento, una distancia d en metros tal que:
a) 7000<d<8000 b) 8000<d<9000 c)
6000<d<7000
d) 9000<d<10000 e) NADA DE LO DICHO
Velocidad del Sonido= 340 m/s
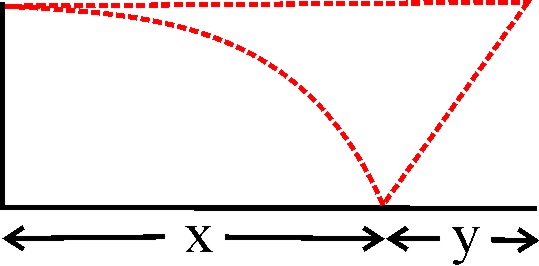
1.4.20. Si lanzas verticalmente hacia arriba
un objeto con una velocidad inicial v y v/g segundos más tarde lanzas otro
con la misma velocidad, si no tienes en cuenta el rozamiento del aire, dirás
que ambos se encuentran:
a)
A LAS 3/4 PARTES DE LA ALTURA MÁXIMA ALCANZADA
b)
AL LLEGAR AL SUELO
c)
A LOS V2/2g SEGUNDOS DE LANZAR EL PRIMER CUERPO
d)
A LOS V2/4g SEGUNDOS DE LANZAR EL SEGUNDO OBJETO
e)
A LA CUARTA PARTE DEL RECORRIDO QUE DEBERIA REALIZAR EL SEGUNDO OBJETO
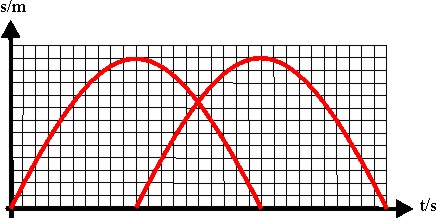
1.4.21. Si,
situado en un extremo de la terraza de un alto edificio, lanzas verticalmente
hacia arriba un objeto, con una velocidad cuyo valor numérico es el triple
del de g, y 4 segundos más tarde dejas caer otro, sin velocidad inicial desde
el mismo sitio, ambos objetos se encontrarán al cabo de un tiempo t del primer
lanzamiento de:
a) 4s b)
8s
c) 10s d) 2s
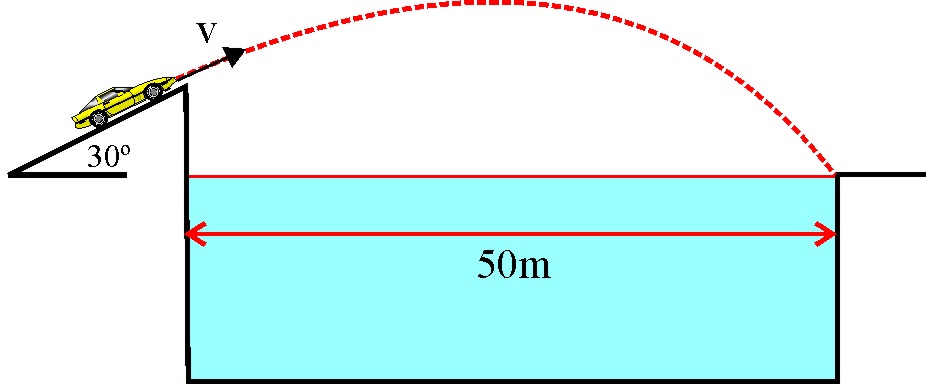
1.4.22.* Si un "coche
fantástico" asciende por una rampa inclinada
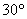 , y cuando está a 4 metros sobre el nivel del suelo "vuela" a fin
de salvar un rio de 50 metros de ancho, para alcanzar la orilla sin "mojarse",
deberá ser impulsado por el turbo antes del "vuelo", con una velocidad
de salida de:
, y cuando está a 4 metros sobre el nivel del suelo "vuela" a fin
de salvar un rio de 50 metros de ancho, para alcanzar la orilla sin "mojarse",
deberá ser impulsado por el turbo antes del "vuelo", con una velocidad
de salida de:
a) 30 m/s b)
126 km/h c) 22,5 m/s
d) 81 km/h
e)NADA DE LO DICHO
1.4.23. Un
bombero desea apagar el fuego en una casa, y para ello deberá introducir agua
por una ventana situada a 10 metros de altura. Si sujeta la manguera a 1 metro
del suelo, apuntándola con un ángulo de
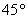 , sobre la pared de cuya fachada dista 15m. Para ello, el módulo de la velocidad
que debe comunicarle al agua la bomba de presión, será en m/s,aproximadamente:
, sobre la pared de cuya fachada dista 15m. Para ello, el módulo de la velocidad
que debe comunicarle al agua la bomba de presión, será en m/s,aproximadamente:
a) 10
b) 19
c) 23
d) 30 e) NINGUNO DE LOS VALORES DADOS
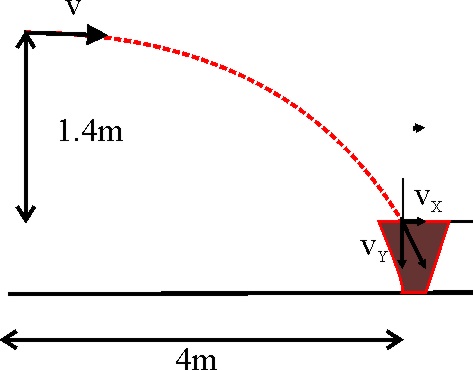
1.4.24.* Un
alumno que se prepara para entrar en la universidad, pensando que está en
el recreo, y congratulándose de su buena forma, intenta encestar en la papelera,
las arrugadas notas que tomó en la clase anterior. Teniendo en cuenta que
está sentado a 4m de aquella, y que la altura de su brazo estirado y vertical,
sobre el nivel del borde de la papelera es de 1,4 metros, para así intentar
superar la cabeza de su compañera de delante, podrás decir que:
a) LA TRAYECTORIA QUE SEGUIRÍAN LOS APUNTES SERÍA
UNA RAMA DE PARÁBOLA
b) LA VELOCIDAD
CON QUE DEBERÍA LANZAR LOS PAPELES PARA ACERTAR EN LA PAPELERA SERÍA DE 7,56
m/s
c) LA VELOCIDAD CON QUE INCIDIRÁN LOS APUNTES EN
LA PAPELERA TIENE POR MÓDULO 9,2 m/s
d) EL ÁNGULO
CON QUE INCIDEN LOS PAPELES, CON LA HORIZONTAL ES DE CERCA DE
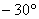
e) EL VECTOR VELOCIDAD FINAL DE LOS PAPELES ES 7,56i-5,3j m/s
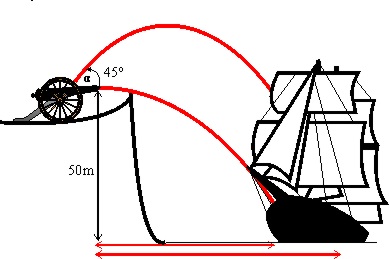
1.4.25.* Hace tan sólo unos años era bastante corriente
ver en televisión películas de piratas. En ellas el barco del capitán (el
pirata "bueno de película") era bombardeado por los cañones de los
fuertes que guardaban el palacio del gobernador de la isla. Los cañones estaban
situados en el acantilado, a 50 metros sobre el nivel del mar. El capitán
pirata después de examinar con el catalejo y suponer que la velocidad de salida
de las balas es de 50 m/s, dice a su contramaestre:
a) LAS BALAS NO NOS DARÁN SI NOS MANTENEMOS A 300
m DE LA COSTA
El contramaestre le responde:
b) TAMPOCO LO HARÍAN SI ESTUVIERAMOS A 170 m
El capitán agrega:
c) COMO LOS CAÑONES NO PUEDEN INCLINARSE NI MAS
DE
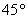 NI MENOS DE
NI MENOS DE
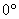 Y TARDAN EN CARGARSE 5 MINUTOS, YO
CREO QUE NI AUNQUE FUERAMOS CAMINANDO NOS DARÍAN
Y TARDAN EN CARGARSE 5 MINUTOS, YO
CREO QUE NI AUNQUE FUERAMOS CAMINANDO NOS DARÍAN
d) SEGURO QUE NOS HUNDEN (contesta el contramaestre)
Te tocará dirimir quién tiene razón y quién
no.
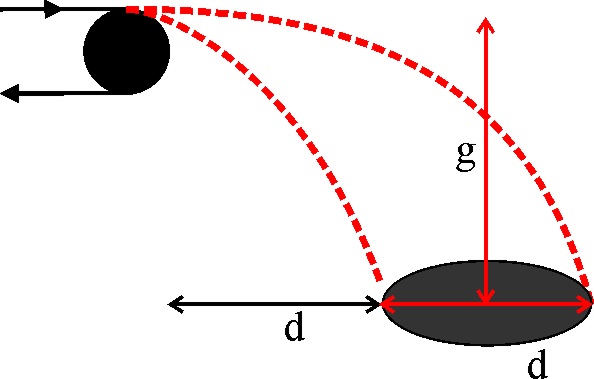
1.4.26. En
una cinta de transporte de mineral que se mueve con una velocidad uniforme
v, situada a una altura h, numéricamente igual a g, sobre la boca de una tolva,
con un diámetro d, cuyo centro dista del borde de la cinta, una distancia
horizontal 3d/2. Para que el mineral caiga dentro, tendrás que decir que v
numéricamente deberá ser:
a) 0,35d<v>d b)
0,7d<v<1,4d
c) 3,5d>v>d d) 1,4d>v>d
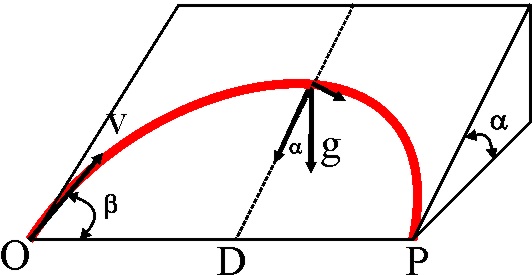
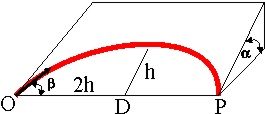
1.4.27. En el esquema de la figura, la relación
entre el seno de 2
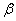 al seno de
al seno de
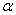 , del sistema para que la esfera que rueda sin rozamiento, lanzada desde O
con velocidad v, alcance P, situado a una distancia D, es de:
, del sistema para que la esfera que rueda sin rozamiento, lanzada desde O
con velocidad v, alcance P, situado a una distancia D, es de:
a) Dg/2v2 b) g/Dv2 c) Dg/v2
d) 2D/gv2 e) NADA DE LO DICHO
1.4.28. En
el laboratorio de mecánica se puede montar un juego muy divertido con canicas,
tal como te indica el montaje de la figura. Se trata de meterla por una abertura
situada a una altura h, mitad de la distancia horizontal al punto de lanzamiento.
Se supone que no hay rozamiento, y que el ángulo de lanzamiento
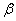 , es doble del de inclinación del plano,
, es doble del de inclinación del plano,
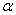 de
de
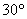 . En estas condiciones el cuadrado del módulo de la velocidad de lanzamiento
deberá ser:
. En estas condiciones el cuadrado del módulo de la velocidad de lanzamiento
deberá ser:
a) 2hg
b) 1,6hg c) 5,5hg d)hg
1.4.29.Si lanzaras
una piedra hacia arriba con un cierto ángulo de forma que en el punto más
alto de su trayectoria el radio de curvatura fuera doble de la altura máxima,
el ángulo de lanzamiento con la horizontal, sería de :
a)
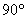 b)
b)
 c)
c)
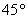
d)
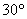 e) NINGUNO DE LOS VALORES DADOS
e) NINGUNO DE LOS VALORES DADOS
1.4. MOVIMIENTO EN EL CAMPO GRAVITATORIO
![]() b)
b)
![]() c)
c)
![]()
![]() e) NADA DE LO DICHO
e) NADA DE LO DICHO![]() b)
b)
![]() c)
c)
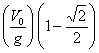
![]() c)
c)
![]()
![]() e) NADA DE LO DICHO
e) NADA DE LO DICHO![]() b)
b)
![]() c)
c)
![]()
![]() e) NINGUNA
DE LAS DADAS
e) NINGUNA
DE LAS DADAS![]() b)
b)
![]() c)
c)
![]()
![]() e) NADA DE LO DICHO
e) NADA DE LO DICHO