Campos vectoriales 1

ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA

sección: TEST DE FÍSICA

5. TEORÍA GENERAL DE CAMPOS

CAMPOS 1

5.1*.Cuando una magnitud escalar varía en el espacio, de un punto a otro, se dice que en ese espacio existe un campo escalar y una de las características de dicho campo es la medida de esta variación, que lo hace a través de su

a) DERIVADA

b) DERIVADA VECTORIAL

c) GRADIENTE

d) INTEGRAL

5.2*.Si en un río echamos corchos a diferente distancia de la orilla, observaríamos que la velocidad con que se moverían debido a la corriente, sería distinta, mayor hacia el centro e inferior cerca de la orilla.

Dirías por lo tanto en el corcho se desplaza en:

a) UN CAMPO DE FUERZAS

b) UN CAMPO DE VELOCIDADES

c) UN CAMPO ESCALAR

d) UN CAMPO VECTORIAL

5.3 Si en tu casa llenas un lavabo con agua, disponiendo un corcho, cerca del borde, y sacando el tapón. El régimen turbillonario del fluido al desaguar, produciría un campo de velocidades cuyo esquema más aproximado de los dados

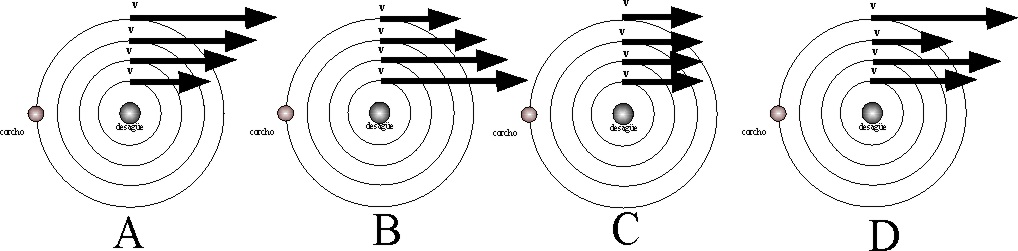
es el:

a) A b) B c) C d) D

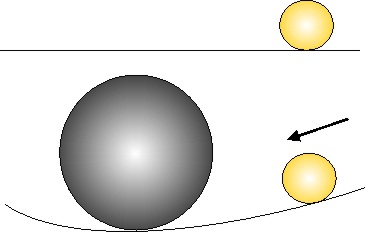
5.4. Por ejemplo, si uno se imagina una tela tensa (sería el espacio del campo vectorial). Si sobre ella se dispone una bolita de cristal, permanecerá en reposo, como su masa es muy pequeña es incapaz de deformar la tela. Sin embargo si en otro punto de la tela se sitúa una bola de acero, ésta sí la deformará, y la bola de cristal se acercará a ella. Por lo tanto, la bola de acero actuará:

a) CREADORA DE UN CAMPO ESCALAR

b) FUENTE DE UN CAMPO

c) MAGNITUD QUE PERTURBA EL MEDIO

d) ORIGEN DE UNA ACCIÓN A DISTANCIA

5.5*. La noción de campo, no afecta únicamente a aquellas magnitudes vectoriales que modifican su valor en el espacio, según su posición. También pueden ser escalares, y en este caso el campo se denominará escalar. Si durante el verano, en tu casa, el sol da en los cristales de tu ventana, y con un termómetro de precisión tomas la temperatura en diferentes puntos, observarás que dentro de la habitación variará en el espacio de unas zonas a otras. En este caso dirás que:

a) EN LA HABITACIÓN EXISTE UN CAMPO ESCALAR

b) LA VARIACIÓN DE LOS VALORES TERMOMÉTRICOS DE UN PUNTO A OTRO CONSTITUYE EL GRADIENTE DE TEMPERATURA

c) EL GRADIENTE DE TEMPERATURA ES DIFERENTE SEGÚN SE TOME MÁS CERCA DE LA VENTANA O MAS LEJOS, MÁS CERCA DE LAS PAREDES O MAS LEJOS

d) EL GRADIENTE DE TEMPERATURA ES UNA MAGNITUD VECTORIAL

5.6*. En el plano XY de la "isla misteriosa" del dibujo, a cada punto del plano dado, le corresponde una determinada altura, dado que es una magnitud escalar, el dibujo realizado debajo corresponde al campo escalar de la función altura y las curvas de nivel, se denominan con carácter general líneas isotímicas que corresponden a:

a) LOS VALORES CONSTANTES DE LA ALTURA

b) EL LUGAR GEOMÉTRICO EN EL QUE LA MAGNITUD REPRESENTADA O SEA LA ALTURA ES LA MISMA

c) LA PENDIENTE DE LA ISLA

d) LAS ZONAS DE IGUAL ALTURA

5.7* .Estamos acostumbrados a escuchar en la información televisiva del tiempo, que cuando las isobaras están muy juntas, los vientos son fuertes, debido a las alteraciones bruscas de presión. Igualmente sabemos que en un mapa topográfico, cuando las curvas de nivel están próximas, el desnivel es mayor, y la zona se supone abrupta. Pues bien, la magnitud que mide la máxima variación de la función escalar considerada, con la variación de la posición, se denomina gradiente, siendo su sentido hacia los valores crecientes de la magnitud escalar que sufre la variación. En el caso de un campo escalar de alturas, el gradiente nos indicaría:

a) LA LÍNEA DE MÁXIMA PENDIENTE

b) LA LÍNEA DE MÍNIMA PENDIENTE

c) LA LÍNEA POR DONDE DISCURRIRÍA LAS AGUAS SALVAJES

d) LA LÍNEA POR DONDE SE BAJARÍA MAS RÁPIDAMENTE

5.8* En los mapas topográficos de una zona montañosa observas unas líneas que corresponden al lugar geométrico de los puntos que tienen la misma altura. Si aplicas la teoría de los campos podrás asegurar que:

a) EL MAPA TRADUCE UN CAMPO ESCALAR DE LA ALTURA

b) LAS LÍNEAS DE IGUAL ALTURA SE DENOMINAN LÍNEAS ISOTÍMICAS

c) EL PLANO DELIMITADO POR LAS LÍNEAS DE IGUAL ALTURA CORRESPONDE A UNA SUPERFICIE CUYOS PUNTOS TIENEN EL MISMO POTENCIAL RESPECTO AL CENTRO DE LA TIERRA

d) EN CUALQUIER PUNTO DE LA LÍNEA DE IGUAL ALTURA, UNA MASA DE UN KILO TENDRÍA LA MISMA ENERGÍA POTENCIAL

e) CUANDO LAS LÍNEAS ESTÁN MAS JUNTAS EL GRADIENTE DE LA ALTURA ES MENOR

5.9*. El gradiente de un campo escalar tiene propiedades muy curiosas puesto que:

a) SIEMPRE ES PERPENDICULAR A CADA PUNTO DE UNA LÍNEA ISOTÍMICA

b) SE CALCULA MEDIANTE LA DERIVADA DE UNA FUNCIÓN ESCALAR RESPECTO A LA POSICIÓN EN UN ESPACIO VECTORIAL DENOMINADA NABLA

c) ES SIEMPRE UN ESCALAR

d) ES 0 EN UNA SUPERFICIE EN LA QUE LA FUNCIÓN ESCALAR ES CONSTANTE

5.10. En un mapa topográfico los arroyos y ríos se observan perfectamente porque suelen estar enmarcados por las líneas isotímicas, en este caso correspondientes a la misma altura, al discurrir sobre valles. Estos ríos y arroyos, debido a la acción del campo gravitatorio:

a) DISCURREN POR LA LINEA DE MÁXIMA PENDIENTE

b) SIGUEN LA MISMA DIRECCIÓN QUE EL GRADIENTE EN CADA PUNTO

c) TIENEN SENTIDO CONTRARIO AL VECTOR GRADIENTE EN CADA PUNTO

d) VAN PERPENDICULARES A LAS LÍNEAS DE IGUAL ALTURA

e) VAN PARALELOS A LAS LÍNEAS DE IGUAL ALTURA

5.11*. Si en un campo escalar de una función que puede ser la temperatura, unes todos los puntos de igual temperatura, formando líneas de nivel, y trazas en cada punto de ellas líneas perpendiculares que corten a aquellas, podrás decir que:

a) LOS VECTORES GRADIENTE DEL CAMPO ESCALAR SERÁN PERPENDICULARES A LAS NUEVAS LÍNEAS

b) LOS VECTORES GRADIENTE DEL CAMPO ESCALAR SERÁN TANGENTES A LAS NUEVAS LÍNEAS

c) SE HABRÁ FORMADO UN CAMPO VECTORIAL DE GRADIENTES

d) LAS LÍNEAS TRAZADAS SON LÍNEAS DEL CAMPO DE GRADIENTES

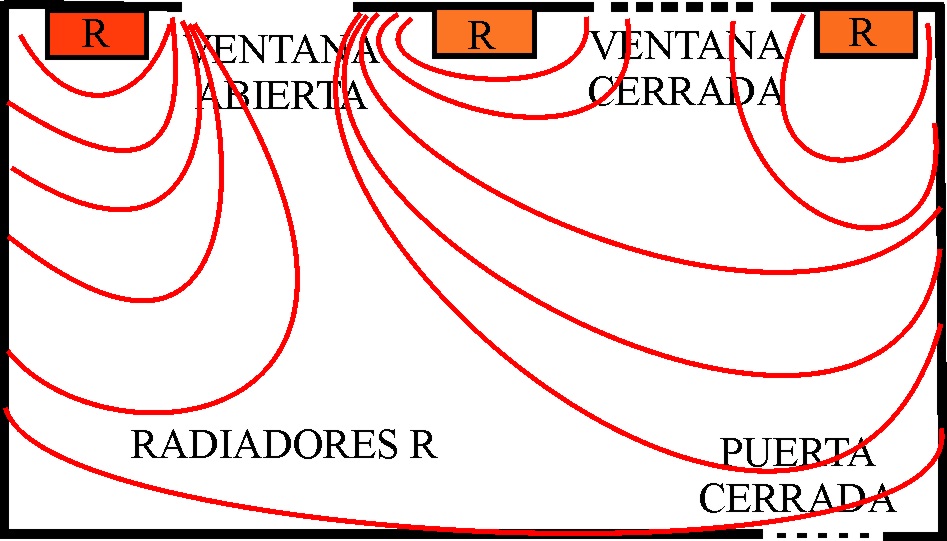
5.12. El dibujo que te dan, corresponde a un aula de física de 8m por 4,5m, en invierno y en la cual se deja una ventana abierta, se toman las temperaturas en cada punto con una sonda sensible y se unen los puntos de igual temperatura con líneas continuas tal como las dadas, que varían en 1ºC. Estudiando dicho dibujo podrás decir que:

a) LAS LÍNEAS TRAZADAS SON ISOBARAS

b) SE TRATA DE UN CAMPO ESCALAR DE TEMPE-RATURAS

c) LOS GRADIENTES MAYORES SE ENCUENTRAN PRÓXIMOS A LA VENTANA CERRADA

d) EL GRADIENTE DE ESE CAMPO SE MEDIRÍA EN ºC/m

5.13*. El término escalar y vectorial aparece por primera vez en los escritos del matemático irlandés Hamilton, así como el de gradiente, que indica grado, escalón, esto es la variación de la función escalar V, pero esta variación tiene carácter vectorial, y por eso deberán aparecer los vectores unitarios (reforzando el carácter vectorial), se conoce con el nombre de nabla y fue representada por primera vez cuando hace referencia a al plano XY como:

a) b)

c) d)

5.14. Si tenemos una función escalar F(x,y,z) , siendo F (presión, temperatura, altura, potencial, densidad electrónica etc.),el gradiente representa las derivadas parciales de dicha función escalar en un espacio vectorial, lo que va a producir una derivada vectorial. Existe un operador vectorial o símbolo matemático que representa dicha operación, consiste en el triángulo (delta) significativo del incremento pero invertido, o sea con el vértice hacia abajo: Por su forma, se le denominó NABLA (el nabla era un instrumento musical de cuerda, tal como el arpa, empleado por sirios y persas), o ATLED (delta al revés). Este operador fue empleado por Hamilton a mediados del siglo XIX. De esta forma,:

a) EL NABLA COMO OPERADOR MATEMÁTICO EN COORDENADAS CARTESIANAS APLICADO A LA FUNCIÓN F SERÍA:

b) QUE TAMBIÉN SE PODRÍA REPRESENTAR POR

c) QUE TIENE POR MÓDULO

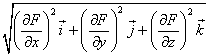
d) MIENTRAS QUE SU DIRECCIÓN SERÁ TAL QUE SUPONGA LA MÍNIMA VARIACIÓN DE LA FUNCIÓN. Y EL SENTIDO DE DICHA VARIACIÓN SIEMPRE SE TOMARÁ EL CRECIENTE.

5.15. El nabla era un instrumento musical parecido a la lira en forma de triángulo muy conocido por sirios y persas. Su forma en contraposición con la de la letra delta, que servía para representar el incremento de una función, se empleó para significar el operador matemático que indica la operación gradiente. Por ello si tienes una función escalar: 2x+3y-5z+1,su nabla te va a dar:

a) 0 EN CUALQUIER PUNTO DEL ESPACIO

b) EN EL PUNTO 1,1,1 , UN VECTOR DE MÓDULO

c) EL VECTOR EN CUALQUIER PUNTO DEL ESPACIO

d) UN VECTOR DE MÓDULO RAÍZ CUADRADA DE -12, EN CUALQUIER PUNTO

5.16. Aunque posiblemente no lo creas el nombre de nabla fue propuesto por el físico matemático escocés Robertson Smith, e inicialmente no se representó con un triángulo equilátero ,(recordando por su forma al instrumento musical cuyo nombre lleva), con el vértice hacia abajo como se conoce actualmente, sino hacia la izquierda. Representa con el símbolo vectorial encima, el cálculo matemático del gradiente. Así si te dicen que calcules el módulo del gradiente de la función escalar V = 2x² + 3y² + z², en el punto (1,1,1), dirías que debería dar:

a) 12

b) 6