ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA

 

ELECTRICIDAD 6. Campo eléctrico 1

 

 

101*. En 1838, Faraday, a través de los experimentos realizados con los campos magnéticos y visualizar como se orientaba el polvillo de hierro en tales campos, sugirió una forma de visualizar los campos de fuerzas, surgiendo lo que denominó línea de fuerza (“línea de fuerza móvil”). Aunque sería Lord Kelvin el que 7 años después fijarías las condiciones que deberían reunir:

a) La intensidad del campo debería ser tangente a ella en cada punto

b) Debería ser la trayectoria de una carga positiva en dicho campo

c) Debería ser la trayectoria de una carga negativa en dicho campo

d) Tendrían que ser perpendiculares a la intensidad del campo en cada punto

 

 

102 * Faraday tratando de unificar la interacción gravitatoria, la eléctrica y la magnética, rebate la teoría de la acción a distancia, diciendo que sólo se trata de la de un punto de fuerza del campo universal, sobre puntos contiguos, y postulando la teoría de la conservación de la fuerza, que sería compatibilizada con las anteriores por Maxwell. Según éste, la intensidad de un campo eléctrico se mide por la fuerza que se ejerce sobre la unidad de carga. Por este motivo:

a) Se medirá en unidades de fuerza

b) Se considerará una energía

c)La intensidad del campo eléctrico se mide en newton/amperios en el SI.

d)La intensidad del campo eléctrico tiene sentido contrario al de la fuerza que actúa sobre la carga negativa

 

 

 

103.Como la intensidad de un campo eléctrico E se define como la fuerza que actúa sobre la unidad de carga positiva, las unidades en las que se mide en el sistema internacional serán:

a) J/C              b) N/C             c) dina/ues      d) dina/C

 

 

 

104*. Dado que la fuerza de interacción eléctrica se mide por la ley de Coulomb, dirás que la expresión que nos dará la variación de intensidad de un campo eléctrico en el aire o vacío vendrá dada en el sistema internacional de unidades por:

a)              b)                c)                 d)

 

 

 

105. La intensidad de un campo eléctrico creado por una carga positiva, en todo su espacio solo será cero:

a) Si la carga es cero             b) Si hay otra carga igual y contraria

c) En el infinito                       d) En el punto cero

 

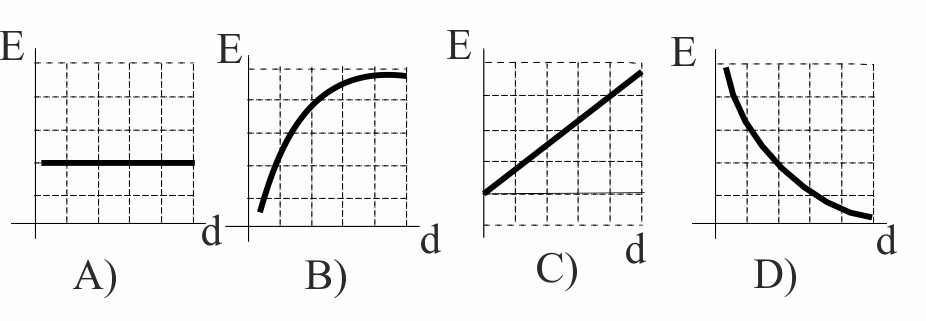
Es la: a) A       b) B                 c) C                 d) D

 

 

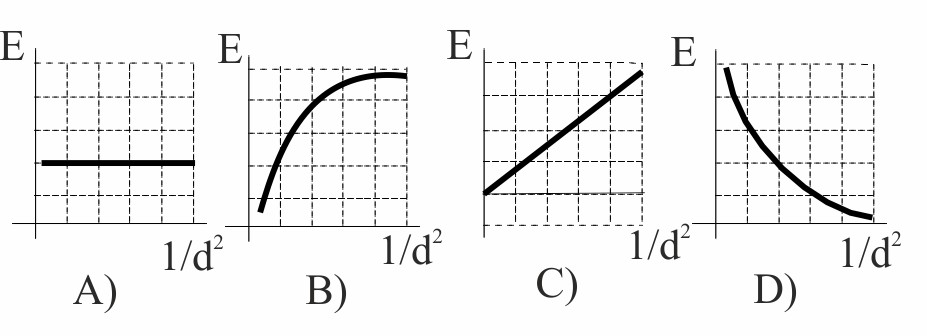
108. Una carga eléctrica positiva puntual crea un campo eléctrico a una distancia d, variable. Se dan las posibles gráficas intensidad del campo eléctrico  en función del inverso del cuadrado de dicha distancia d.

 

 

De todos los dados, será el: a) A       b) B                 c) C                 d) D

 

 

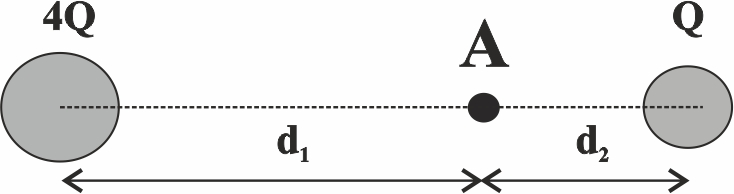
110. Sabiendo que el campo eléctrico en A, es nulo, la relación entre d₁ y d₂, deberá ser:

a)1                  b)4                  c)2                   d)0,5

 

 

 

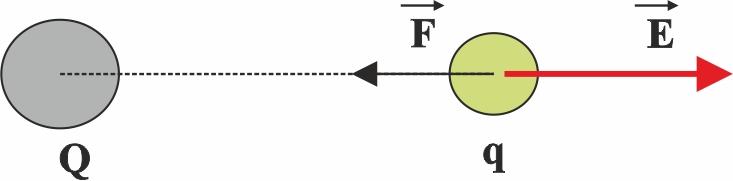
109. Si Q y q, son dos cargas puntuales aisladas, para que se cumpla lo que se ve en el dibujo, deberá ocurrir que:

a) Q<0 y q<0             b) Q<0 y q>0

c)Q>0 y q<0              d) Q>0 y q>0

 

 

 

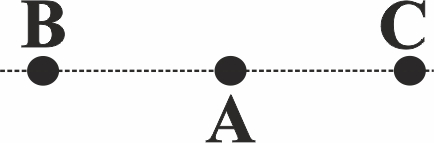
111.Dos cargas puntuales Q₁ y Q₂ de signos opuestos están situadas respectivamente en A y B, sabiendo que numéricamente Q₁>Q₂, podremos asegurar que existe un punto en el eje x, en el que el campo eléctrico resultantes es nulo. Dicho punto estará:

a)  Entre A y B                       b) A la derecha de B              

c) A la izquierda de A             d) Coincide con A

 

 

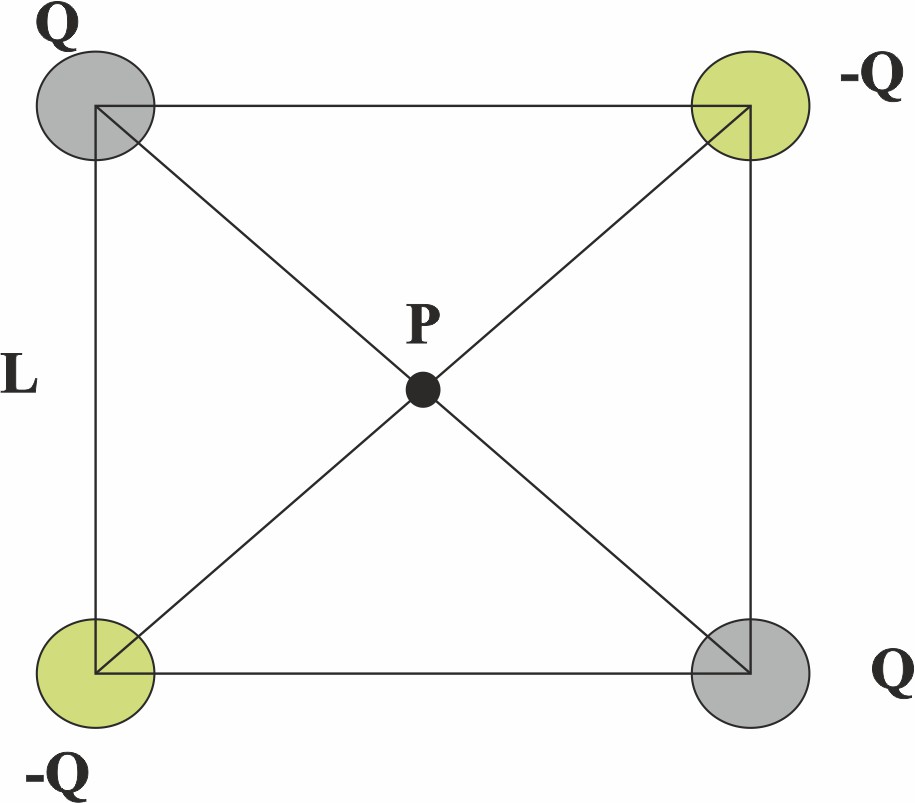
116. Sobre un cuadrado de lado L, se sitúan las cargas que indica el dibujo. La intensidad del campo eléctrico en el punto P será:

a) 4KQ/L²                   b) 2KQ/L                    c) KQ/L²                     d) 0

mientras que su sentido estará orientado:

a)      Hacia abajo                     b) Hacia arriba         

c) Hacia la derecha                d) Hacia la izquierda

 

 

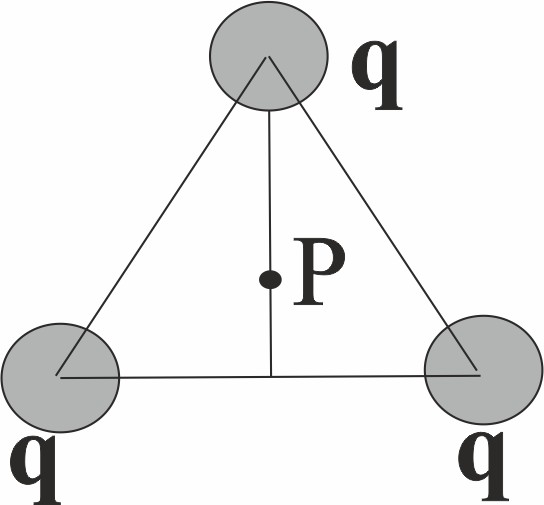
120. Tres cargas puntuales e iguales, se disponen en los vértices de un triángulo equilátero. El vector que indica su campo eléctrico creado en su centro P, será:

a) Un vector vertical dirigido hacia arriba

b)Un vector vertical dirigido hacia abajo

c)Un vector horizontal dirigido hacia la derecha

d)Nulo

 

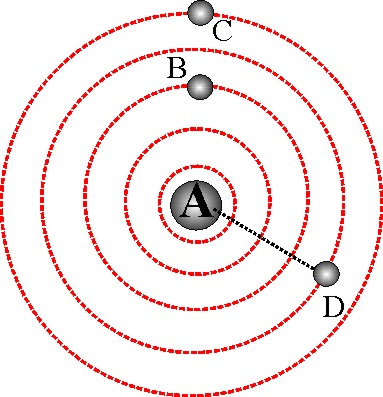
106. En las proximidades de A que es una carga eléctrica positiva , se sitúan 3 partículas B, C y D. A C no le ocurre nada. B es atraída hacia A y D se aleja hasta el infinito. Según todo ello podrás asegurar que:

a) D es una masa

b) C no es una carga eléctrica

c) La acción de a sobre d en el infinito es 0

d) B es una carga positiva

 

 

 

107.De las gráficas dadas, la que mejor corresponde con la definición de campo eléctrico:

 

 

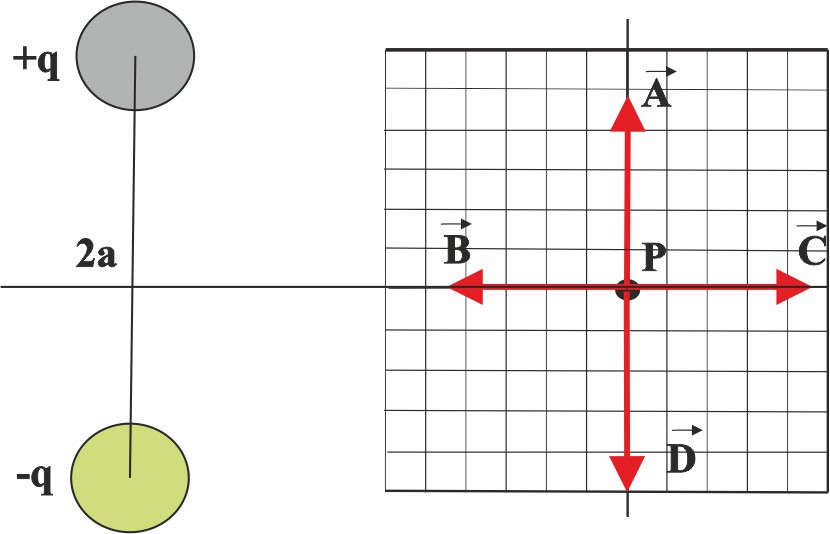
119. Dos cargas puntuales separadas una distancia muy  pequeña 2a, tal como muestra la figura, se suelen denominar dipolo. El campo que crean las mismas en el punto P, será un vector orientado como se indica en :

a) A                              b) B                          

c)C                              d)D

 

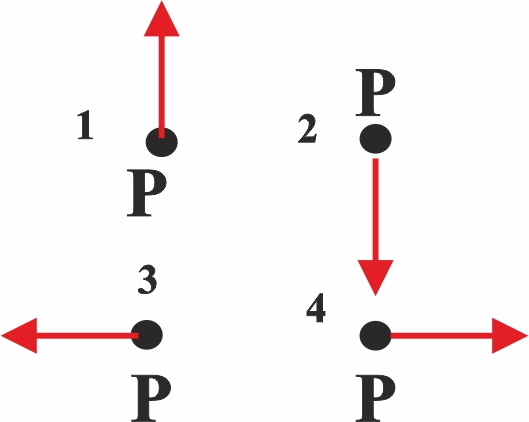
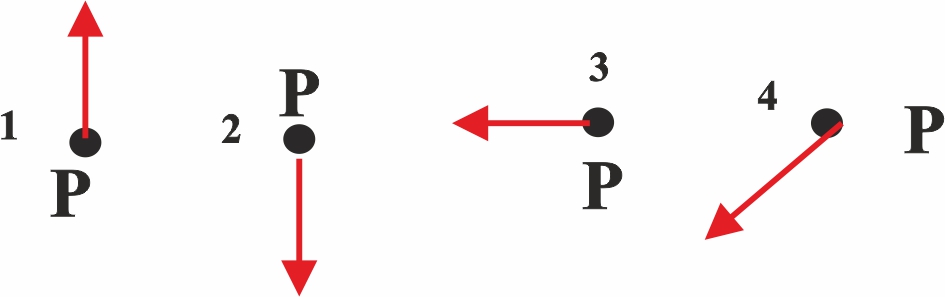
113.En la figura, Q representa una carga puntual positiva, y P un punto próximo a ella. El campo eléctrico que mejor representaría de todos los dados sería el:

a)1                   b) 2                  c)3                   d)4

 

 

114. Una carga puntual crea un campo eléctrico a una distancia d. Para que el campo eléctrico tenga una intensidad cuatro  veces mayor, la distancia de la carga deberá ser:

a) 2d               b) d/4              c) d/2               d) d√2

 

 

 

 

115. Para que una  partícula de masa m y carga Q(Q<0), permanezca en equilibrio estático deberá abandonarse en un campo eléctrico:

a) Vertical con sentido hacia abajo               b) Vertical con sentido hacia arriba

c) Horizontal  hacia la derecha                     d) Horizontal y hacia la izquierda

 

 

 

112. En A existe un campo eléctrico orientado hacia C. Si en este punto se sitúa una carga puntual negativa, ésta quedará sometida a una fuerza orientada:

a) Hacia B      b) Hacia C     

c) perpendicular a BC y hacia arriba

d) Perpendicular a BC y hacia abajo

 

 

 

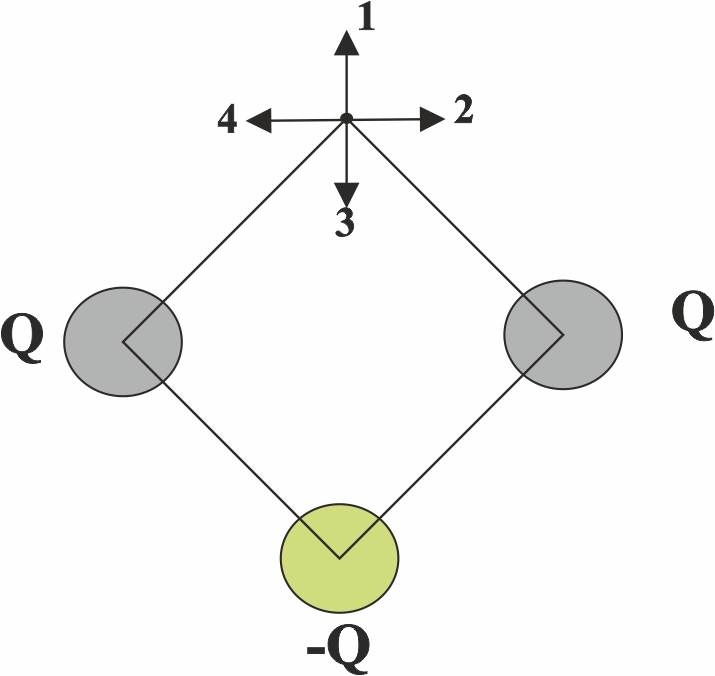
118. Sobre los 3 vértices de un rombo, se sitúan las cargas que indica el dibujo. La intensidad del campo eléctrico en el punto P será un vector orientado, tal como se indica en: 

a) 1                  b)2                  c)3                   d)4

                            

 

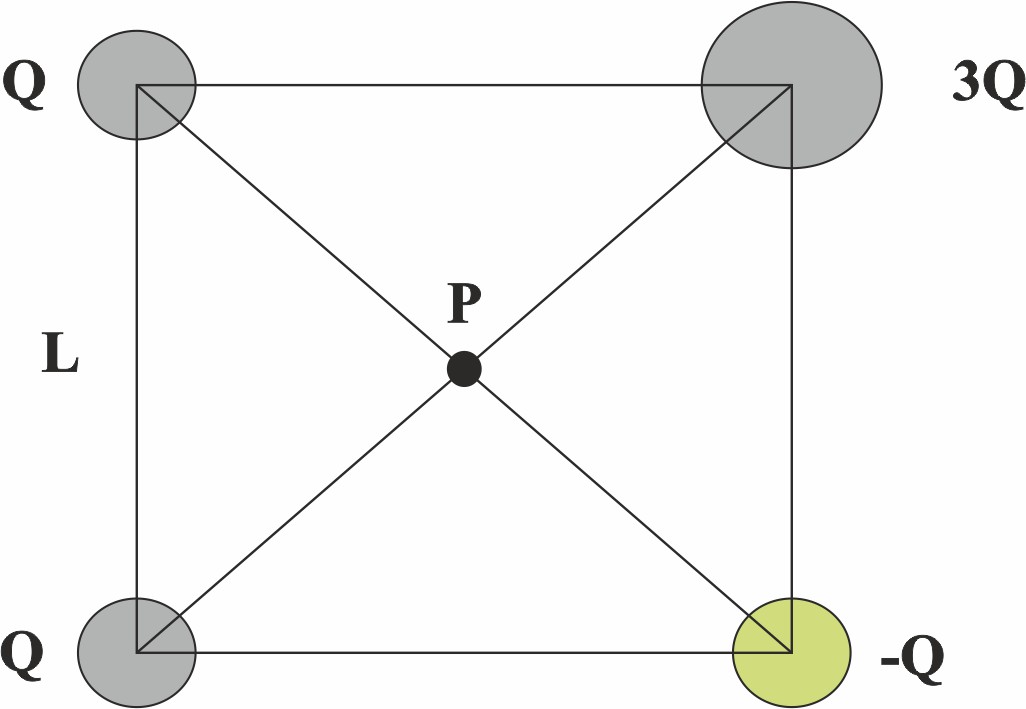
117. Sobre un cuadrado de lado L, se sitúan las cargas que indica el dibujo.

La intensidad del campo eléctrico en el punto P será:

a) 4KQ/L²                   b) 2KQ/L²                   c) KQ/L²         d) 4KQ√2/L²

y será  un vector orientado, tal como se indica en el dibujo inferior:          

a) 1      b)2                  c)3                   d)4