ENSEÑANZA
DE LA FÍSICA Y LA QUÍMICA
3.4. SISTEMA
DE REFERENCIA DEL CENTRO DE MASAS (I)
3.4.1.* Respecto del sistema de referencia
del centro de masas (S.R.C.M.) podemos decir que
a) ES
INERCIAL EN LOS SISTEMAS AISLADOS
b) EL
ORIGEN DEL S.R.C.M. ES EL CENTRO DE MASAS DEL SISTEMA
c) EN MUCHOS SISTEMAS
EL CENTRO DE MASAS Y EL CENTRO DE GRAVEDAD COINCIDEN
d) EN UN SISTEMA
DE PARTÍCULAS DISCRETAS EL ORIGEN DEL S.R.C.M. ESTÁ NECESARIAMENTE LOCALIZADO
SOBRE UNA DE LAS PARTÍCULAS
e) EL SISTEMA DE
REFERENCIA DEL LABORATORIO (S.R.L.) ES EL MISMO QUE EL S.R.C.M.
3.4.2. La cantidad de movimiento de un sistema de partículas
referido al sistema del centro de masas es:
a)
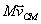 , SIENDO M LA MASA DEL SISTEMA Y
, SIENDO M LA MASA DEL SISTEMA Y
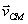 SU VELOCIDAD EN UN SISTEMA DE REFERENCIA DE LABORATORIO
SU VELOCIDAD EN UN SISTEMA DE REFERENCIA DE LABORATORIO
b) LA MISMA QUE
SI SE TOMA COMO REFERENCIA UN SISTEMA INERCIAL CUALQUIERA
c) NULA
d) VARÍA CON EL
TIEMPO
3.4.3. El sistema de referencia del centro de masas suele
denominarse a veces, sistema de momento lineal nulo, esto se debe a que en
él:
a) LA CANTIDAD
DE MOVIMIENTO
DE CADA UNO LOS PUNTOS MATERIALES ES SIEMPRE 0
b) TODOS LOS PUNTOS
MATERIALES REFERIDOS ESTÁN EN REPOSO
c) TODOS LOS PUNTOS
MATERIALES TIENEN IGUAL MOMENTO LINEAL
d) LA SUMA DE LA
CANTIDAD DE MOVIMIENTO DE TODOS LOS PUNTOS ES NULA
e) TODOS LOS PUNTOS MATERIALES
TIENEN LA MISMA MASA
3.4.4. * Las magnitudes físicas relativas a un sistema
de puntos materiales que tienen el mismo valor cuando se miden desde un sistema de referencia
de laboratorio o desde un sistema de referencia del centro de masas pueden
ser:
a) LA MASA DE LOS
PUNTOS MATERIALES
b) LA DISTANCIA
DE CADA
PARTÍCULA AL ORIGEN DE CUALQUIER SISTEMA
c) LAS FUERZAS
QUE ACTUEN EXTERNAMENTE
d) LA VELOCIDAD
CON QUE SE DESPLAZAN
e) LA ENERGÍA CINÉTICA
3.4.5. * El sistema de referencia del centro de masas
es un sistema de referencia interno de un sistema de partículas que permite
justificar acciones interiores que serían inobservables en un sistema de referencia
de laboratorio. Sin embargo en un sistema de partículas múltiples en estado
de movimiento, el centro de masas con toda la masa del sistema situada en
él:
a) TIENE SIEMPRE
UN MÓDULO DE LA VELOCIDAD MENOR QUE CUALQUIER PARTÍCULA, EN EL SISTEMA DE
REFERENCIA DE LABORATORIO
b) TIENE SIEMPRE
UN MÓDULO DE LA VELOCIDAD MENOR QUE CUALQUIER PARTÍCULA CUANDO SE FIJA
EN EL S.R.C.M.
c) SU VELOCIDAD,
MEDIDA EN UN S.R.L., MULTIPLICADA POR LA MASA DEL SISTEMA NOS MIDE LA CANTIDAD DE MOVIMIENTO.
d) PERMANECE SIEMPRE
EN REPOSO SEA CUAL SEA EL SISTEMA DE REFERENCIA
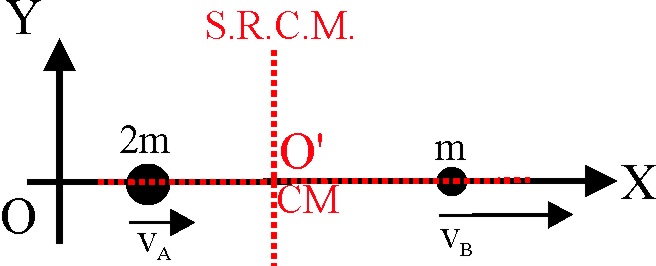
3.4.6. Si dos puntos materiales
A y B, se mueven por el eje X, del laboratorio, en su sentido positivo, B
con doble velocidad que A, que a su vez, tiene doble masa que B, en el sistema
de referencia del centro de masas:
a) A Y B TENDRÍAN
IGUAL VELOCIDAD
b) B TENDRÍA DOBLE
VELOCIDAD QUE A
c) B TENDRÍA DOBLE
VELOCIDAD QUE A PERO CON SENTIDO CONTRARIO
d) A CAMBIARÍA
DE SENTIDO SU VELOCIDAD
e) A TENDRÍA DOBLE
VELOCIDAD QUE B
3.4.7.* Cuando un sistema
de partículas está constituido por sólo dos, A y B, es muy conveniente emplear
el concepto de masa reducida
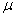 , esto es, el producto de sus masas dividido por la suma de ellas, y
considerarlo como si se tratara de una sola partícula, que se moviera con
la velocidad relativa de una partícula respecto a la otra. Usando estos términos,
podrás asegurar que en el sistema de referencia del centro de masas:
, esto es, el producto de sus masas dividido por la suma de ellas, y
considerarlo como si se tratara de una sola partícula, que se moviera con
la velocidad relativa de una partícula respecto a la otra. Usando estos términos,
podrás asegurar que en el sistema de referencia del centro de masas:
a)
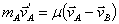 b)
b)
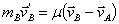
c)
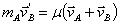 d)
d)
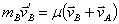
e)
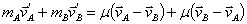
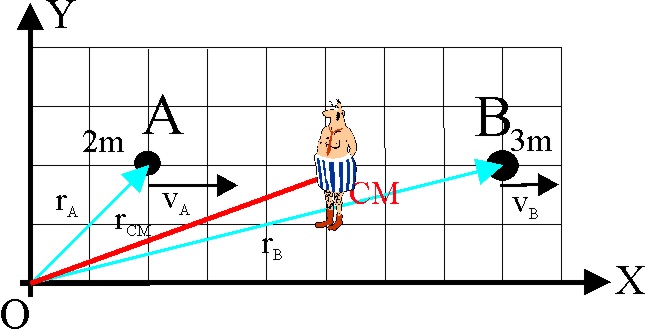
3.4.8. * Dos partículas A
y B, de masas 2m y 3m, se encuentran en un sistema de referencia de laboratorio
en los puntos respectivos (2,2) y (8,2) en m. Comienzan a moverse con velocidades
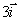 y
y
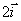 m/s. Si situáramos un observador en el centro de masas
del sistema diría que:
m/s. Si situáramos un observador en el centro de masas
del sistema diría que:
a) A ESTÁ A UNA
DISTANCIA DE 3,6m DE ÉL
b) EL VECTOR DE
POSICIÓN DE B RESPECTO DEL OBSERVADOR ES:
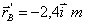
c) B SE ACERCARÍA
A ÉL
d) A SE ALEJARÍA
DE ÉL CON UNA VELOCIDAD DE
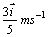
3.4.9.* La velocidad relativa
de una partícula A, de masa 2M, respecto a otra partícula B de masa M, en
el sistema de referencia del centro de masa es:
a) SIEMPRE MAYOR
QUE LA RELATIVA EN EL SISTEMA DE REFERENCIA DE LABORATORIO
b) IGUAL A LA RELATIVA
EN EL SISTEMA DE REFERENCIA DE LABORATORIO
c) IGUAL EN MÓDULO
A LA RELATIVA EN EL SISTEMA DE REFERENCIA DE LABORATORIO, PERO TIENE SENTIDO
CONTRARIO
d) INDEPENDIENTE
DE LA MASA DE LAS PARTÍCULAS
3.4.10. Dos partículas de
masas m1= 1kg y m2= 3kg se desplazan respecto a un sistema
inercial con las velocidades v1= 4ti m/s y v2=
4t2j m/s. La velocidad de la partícula 1, expresada en m/s,
respecto al centro de masas es:
a)
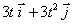 b)
b)
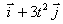 c)
c)
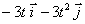 d) CERO
d) CERO
y la de la partícula 2 es:
a)
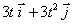 b)
b)
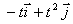 c)
c)
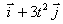 d)
CERO
d)
CERO
3.4.11.* Tres partículas
de masas A, B y C, de masas respectivas, m, 2m y 3m, se encuentran en reposo,
en un sistema de referencia de laboratorio en los puntos (1,0,0), (0,1,0)
y (0,0,1). Sobre ellas e independientemente actúan las fuerzas exteriores:
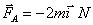 ,
,
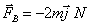 y
y
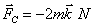 . De este sistema, cuyas
magnitudes están medidas en el S.I., podrás decir que:
. De este sistema, cuyas
magnitudes están medidas en el S.I., podrás decir que:
a) SU CENTRO DE
MASAS NO SE MUEVE
b) EN EL SISTEMA
DE REFERENCIA DE LABORATORIO, LA VELOCIDAD DE A RESPECTO DE B, AL CABO DE 0,1s ES -
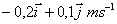
c) LA VELOCIDAD
DE A EN EL SISTEMA DEL CENTRO DE MASAS TIENE POR MÓDULO APROXIMADAMENTE 0,18 m/s
d) LA VELOCIDAD
DE A RESPECTO A B AL CABO DE 0,1s EN EL SISTEMA DE REFERENCIA DEL CENTRO DE
MASAS ES
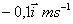
e) LA POSICIÓN
DE C RESPECTO AL CENTRO DE MASAS AL CABO DE 1s ES
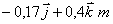
3.4.12. Un sistema de tres
partículas tienen respecto de su centro de masas unas cantidades de movimiento
que valen
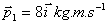 ,
,
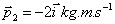 y
y
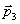 . El valor
de
. El valor
de
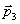 , expresado en
, expresado en
kg.m.s-1 es:
a) 6
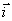 b) -6
b) -6
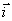 c)
2
c)
2
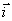 d)
-2
d)
-2
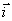 e)
-8
e)
-8
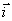
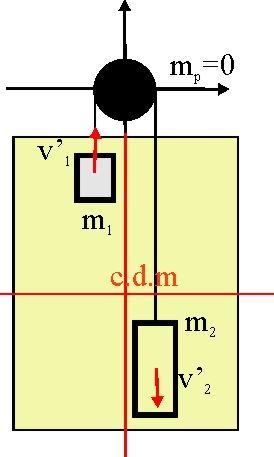
3.4.13. En el sistema de
la figura la masa m2 es tres veces mayor que la m1.
La velocidad de la masa m1, expresada en m/s, respecto del sistema
del centro de masas vale al cabo de 5 segundos:
a)
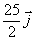 b)
b)
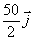
c)
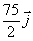 d) CERO
d) CERO
y la de la masa m2:
a)
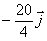 b)
b)
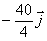
c)
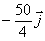 d) CERO
d) CERO
tómese g=10ms-2
3.4.14. En el ejercicio anterior
la cantidad de movimiento del sistema, expresada en kg.m/s (tomando m1=1kg) respecto del sistema inercial de referencia
es:
a)
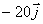 b)
b)
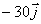 c)
c)
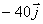 d)
d)
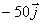 e) CERO
e) CERO
y la cantidad de movimiento del sistema
ligado al centro de masas vale:
a)
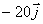 b)
b)
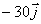 c)
c)
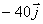 d)
d)
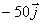 e) CERO
e) CERO
mientras que la cantidad de movimiento de
la masa m2 respecto del sistema del centro de masas es:
a)
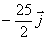 b)
b)
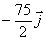 c)
c)
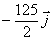 d)
d)
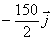 e) CERO
e) CERO
3.4.15. Un sistema de partículas
formado por tres de ellas tienen las masas y velocidades expresadas en el
dibujo respecto del sistema del centro de masas, se deduce que la velocidad
de la tercera partícula, expresada en m/s, respecto al sistema citado es:
a)
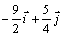 b)
b)
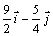
c)
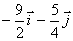 d) CERO
d) CERO
![]() , SIENDO M
, SIENDO M ![]() SU VELOCIDAD EN UN SISTEMA DE REFERENCIA DE LABORATORIO
SU VELOCIDAD EN UN SISTEMA DE REFERENCIA DE LABORATORIO