Choque II

3.5.37*.La partícula A de masa m y velocidad m/s, colisiona elásticamente con B, de masa 4m, situada en reposo, en un sistema de referencia de laboratorio. En el sistema de referencia del centro de masas, podrás asegurar que:

a) LA VELOCIDAD DE A ANTES DEL CHOQUE ES m/s

b) LA VELOCIDAD DE B DESPUÉS DEL CHOQUE ES m/s

c) LA VELOCIDAD DE A DESPUÉS DEL CHOQUE, RESPECTO A LA QUE TENÍA ANTES DEL CHOQUE ES m/s

d) LA VELOCIDAD DE B DESPUÉS DEL CHOQUE, ES DOBLE DE LA QUE TENDRÍA EN UN SISTEMA DE LABORATORIO

3.5.38*.La partícula A, de masa 4m, tiene un vector de posición, , mientras que la B, de masa 6m, , en unidades del SI, y en un sistema de referencia de laboratorio. De este sistema y con estos datos podrás decir que:

a) EL CENTRO DE MASAS DEL SISTEMA SE MUEVE CON UN MUA CON a=0,4 m/s²

b) CHOCARÁN AL CABO DE 1s

c) EL VECTOR DE POSICIÓN DEL LUGAR DE LA COLISIÓN SERÁ m.

d) SI EL CHOQUE ES ELÁSTICO LA VELOCIDAD DE A, DESPUÉS DE LA COLISIÓN ES m/s

e) SI EL CHOQUE ES ELÁSTICO LA VELOCIDAD DE B EN EL SISTEMA DE REFERENCIA DEL CENTRO DE MASAS ES m/s.

3.5.39*. Si la colisión anterior fuera perfectamente inelástica, dirías que:

a) LA VELOCIDAD DE B DESPUÉS DE LA COLISIÓN, EN EL SISTEMA DE REFERENCIA DE LABORATORIO ES m/s.

b) LA ENERGÍA PERDIDA EN LA COLISIÓN INELÁSTICA ES DE 43,2m J.

c) LA VELOCIDAD DE B DESPUES DE LA COLISIÓN, EN EL SISTEMA DE REFERENCIA DEL CENTRO DE MASAS ES 0

d) LA VELOCIDAD DE A DESPUÉS DE LA COLISIÓN, EN EL SISTEMA DE REFERENCIA DEL CENTRO DE MASAS ES IGUAL A LA DE B

3.5.40. Si la partícula A colisiona con la B en un choque completamente inelástico contemplado en el sistema de referencia del centro de masas, podrás asegurar que:

a) LA VELOCIDAD FINAL DE A NO ES LA MISMA QUE LA DE B

b) LA VELOCIDAD DEL SISTEMA DESPUÉS DE LA COLISIÓN ES NULA

c) LA PERDIDA DE ENERGÍA CINÉTICA ES IGUAL A LA ENERGÍA QUE TENÍAN LOS CUERPOS ANTES DE LA COLISIÓN EN DICHO SISTEMA DE REFERENCIA

d) EL VECTOR DE POSICIÓN DEL CENTRO DE MASAS DEL SISTEMA NO VARÍA

e) LA ENERGÍA INICIAL DEL SISTEMA ES IGUAL A LA MITAD DE LA MASA REDUCIDA, POR EL CUADRADO DE LA VELOCIDAD RELATIVA DE LAS PARTÍCULAS COLISIONANTES.

3.5.41*. El coeficiente de restitución fue definido por Newton en las colisiones directas como la relación entre las velocidades relativas de los colisionantes después del choque, y las velocidades relativas antes del choque, con el signo negativo. De él también puedes decir que:

a) ES LA RELACIÓN ENTRE LA SUMA DE LAS VELOCIDADES DE CADA CUERPO ANTES Y DESPUÉS DEL CHOQUE

b) ES LA RELACIÓN ENTRE EL CUADRADO DE LA ENERGÍA FINAL Y LA ENERGÍA INICIAL, EN DETERMINADAS CONDICIONES

c) ES UNA MAGNITUD SIN UNIDADES

d) ES CERO, EN UN CHOQUE PERFECTAMENTE ELÁSTICO

3.5.42. La pérdida relativa de energía en una colisión parcialmente inelástica entre dos cuerpos A y B, de masas respectivas M y 4M, y velocidades v_A y nula, con un coeficiente de restitución 1/2 es:

a) INDEPENDIENTE DE LAS VELOCIDADES DE A Y B

b) 40% c) 50% d) 60%

3.5.43*. Si el coeficiente de restitución de la colisión de una esfera metálica con el suelo es 0,5, podrás asegurar que:

a) DEJADA CAER DESDE UNA ALTURA H REBOTARA HASTA H/2

b) DEJADA CAER DESDE UNA ALTURA H REBOTARA HASTA H/4

c) EL MÓDULO DE SU VELOCIDAD DESPUÉS DEL CHOQUE ES LA MITAD DEL MÓDULO DE SU VELOCIDAD ANTES DEL CHOQUE

d) EL MÓDULO DE SU VELOCIDAD DESPUÉS DEL CHOQUE ES LA CUARTA PARTE DEL MÓDULO DE SU VELOCIDAD ANTES DEL CHOQUE

3.5.44. Si dos esferas A y B, de igual masa y material se desplazan al encuentro una de la otra, con velocidades respectivas v_A y v_B, y teniendo coeficiente de restitución e, podrás asegurar que la esfera A o la B, se detendrán después de la colisión cuando las relaciones entre las velocidades de A y B antes del choque sean:

a) (1+e) ; -(1+e)

b) (1+e)/(1-e) ; -(1+e)/(1-e)

c) -(1+e)/(1-e) ; -(1-e)/(1+e)

d) (1-e); (1+e)

3.5.45. Si se suelta una esfera metálica A, desde una altura H, colisionando con el suelo de forma que su coeficiente de restitución es e, y bota repetidas veces hasta que se detiene, el camino recorrido por A hasta que se detiene será:

a) H/(1+e²) b) [(1+e²)/(1-e²)]H c) H/(1-e²) d)[(1-e²)/(1+e²)]H

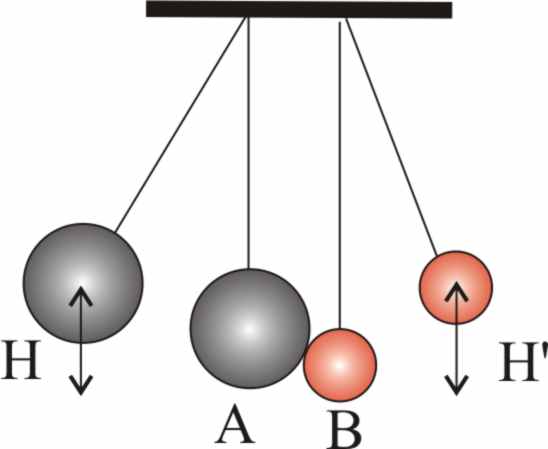
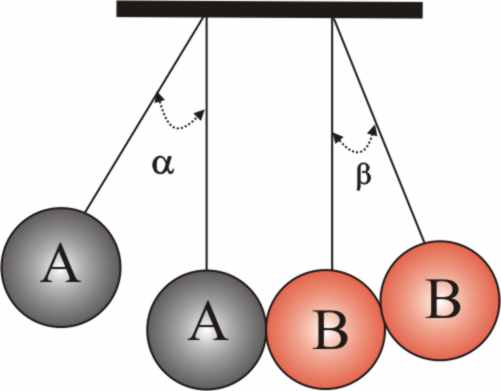
3.5.46. Si dispones de 2 esferas A y B, de igual masa, en sendos péndulos de igual longitud L, y paralelos. Separas A un cierto ángulo y la suelta, con lo que colisiona con B con un coeficiente de restitución e, de tal forma que B se separa formando otro ángulo

. Podrás decir que en dicha colisión la relación entre los senos de los ángulos mitades de y es :

a) e b) 2/(1+e) c) (1+e)/2 d) 2/(1 -e)

3.5.47. Si dispones de 2 esferas, A de masa 2m y B de masa m, en sendos péndulos de igual longitud L, y paralelos. Separas A hasta que alcance una altura H, y la sueltas, golpeando con B, con un coeficiente de restitución e. La altura H', alcanzada por B en dicha colisión será:

a) 4(1+e)²H/9

b)(1+e²)4H/9

c) 4(1-e)²H/9

d)(1+e²)H/9

3.5.48. En un choque frontal entre dos esferas A y B, de masas iguales con velocidades iguales y de sentido contrario, el porcentaje de pérdida de energía respecto a la inicial, cuando el coeficiente de restitución es e, es:

a) 100 (1-e)

b) 100(1+e²)

c) 100(1-e²)

d) 100 (1+e)/2

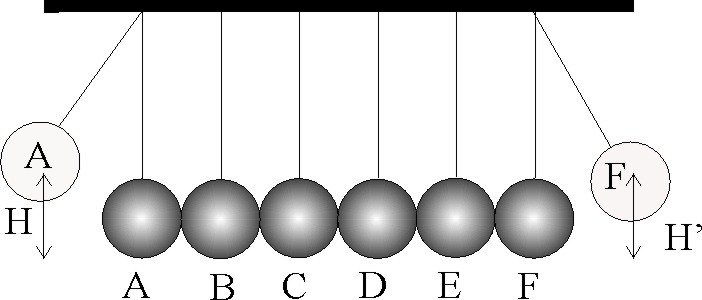
3.5.49. el francés Mariotte a mediados del XVIII, hizo un experimento curioso. Disponiendo de 6 péndulos alineados y pegados, y elevándolo el de la izquierda una altura H, y soltándolo, el del otro extremo se elevó hasta una altura H’. Si el coeficiente de restitución en la colisión fuera 0,8 la relación entre H y H' sería aproximadamente:

a) 2 b) 5 c) 9 d) 12

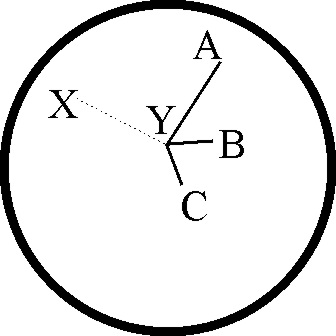
5.50. Un meteorólogo escocés Wilson, descubre al comenzar el siglo XX, que cuando pasa una descarga eléctrica a través de una zona de vapor de agua saturado, en su camino va produciendo núcleos de condensación, pequeñas gotitas perfectamente visibles, y que se pueden fotografiar. Crea así la cámara que lleva su nombre, que desempeñará un papel fundamental en la investigación sobre la estructura atómica, y cuyo desarrollo proporcionará nada menos que 3 Nobel de Física, en 1927, 48 y 60. Teniendo en cuenta que las huellas dependen de la carga y de la masa de las partículas de una reacción nuclear, si en una cámara de Wilson se aprecia el rastro indicado que corresponde a la colisión entre una partícula desconocida X y que no deja huella, con unos núcleos en reposo A, podrás decir que:

a)     EL NÚCLEO EN REPOSO SE ROMPE EN DOS FRAGMENTOS DE IGUAL MASA

b)    LA COLISIÓN PRODUCIDA FUE COMPLETAMENTE INELÁSTICA

c)  LA COLISIÓN ES PERFECTAMENTE ELÁSTICA Y LA PARTÍCULA X REBOTA CON VELOCIDAD DE IGUAL MÓDULO

d)    EN LA COLISIÓN EL NÚCLEO A SE FRAGMENTA EN DOS DE MUY DIFERENTE MASA

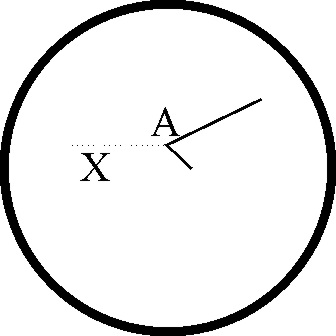
5.51. Cuando la huella en una cámara de Wilson modificada, es más larga y gruesa, indica que la partícula tiene más masa. Si te dan la fotografía de un proceso nuclear que corresponde a la colisión de una partícula invisible X, por no tener carga, con otra mucho más másica Y en reposo, podrás decir de las huellas dadas A, B, y C que:

           a) X SE ESCINDIÓ EN TRES FRAGMENTOS

           b) DOS DE LOS FRAGMENTOS TIENEN IGUAL MASA Y CARGA

           c) LA MASA DE C ES MAYOR QUE LA DE A Y B

           d) EN EL PROCESO NO SE CONSERVA LA ENERGÍA NI LA CANTIDAD DE MOVIMIENTO

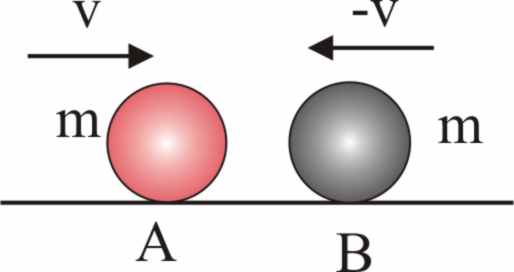
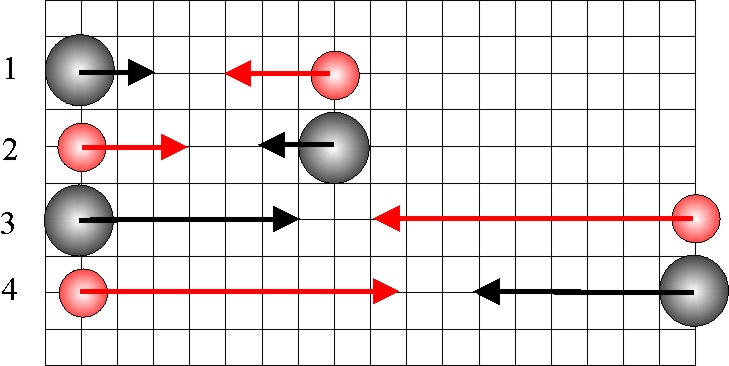
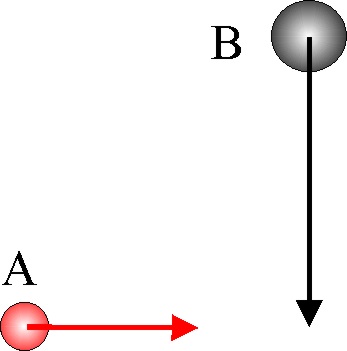
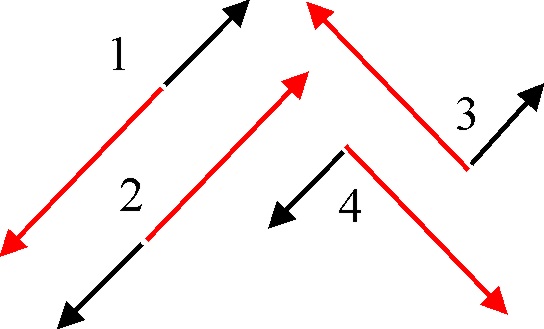
3.5.28. El esquema que te dan corresponde al movimiento unidimensional de dos esferas A (negra) y B (roja), de masas respectivas 3 y 2 kg, sobre una mesa sin rozamiento y cuyos vectores velocidad son los dibujados (cada cuadrado una unidad SI), suponiendo que la colisión que efectúan sea elástica, los vectores velocidad de A y B, respectivamente antes de la colisión en un sistema de referencia del centro de masas serán de los esquematizados:

a) el 1

b) el 2

c) el 3

d) el 4

3.5.29. El esquema que te dan corresponde al movimiento unidimensional de dos esferas A (negra) y B (roja), de masas respectivas 3 y 2 kg, sobre una mesa sin rozamiento y cuyos vectores velocidad son los dibujados (cada cuadrado una unidad SI), suponiendo que la colisión que efectúan sea elástica, los vectores velocidad de A y B, respectivamente antes de la colisión en un sistema de referencia del centro de masas serán de los esquematizados:

a) el 1

b) el 2

c) el 3

d) el 4

3.5.30. El esquema que te dan corresponde al movimiento unidimensional de dos esferas A (negra) y B (roja), de masas respectivas 3 y 2 kg, sobre una mesa sin rozamiento y cuyos vectores velocidad son los dibujados (cada cuadrado una unidad SI), suponiendo que la colisión que efectúan sea elástica, los vectores velocidad de A y B, respectivamente después de la colisión en un sistema de referencia del centro de masas serán de los esquema-tizados:

a) el 1

b) el 2

c) el 3

d) el 4

3.5.31. El esquema que te dan corresponde al movimiento unidimensional de dos esferas A (negra) y B (roja), de masas respectivas 3 y 2 kg, sobre una mesa sin rozamiento y cuyos vectores velocidad son los dibujados (cada cuadrado una unidad SI), suponiendo que la colisión que efectúan sea elástica, los vectores velocidad de A y B, respectivamente después de la colisión en un sistema de referencia del centro de masas serán de los esquematizados:

a) el 1

b) el 2

c) el 3

d) el 4

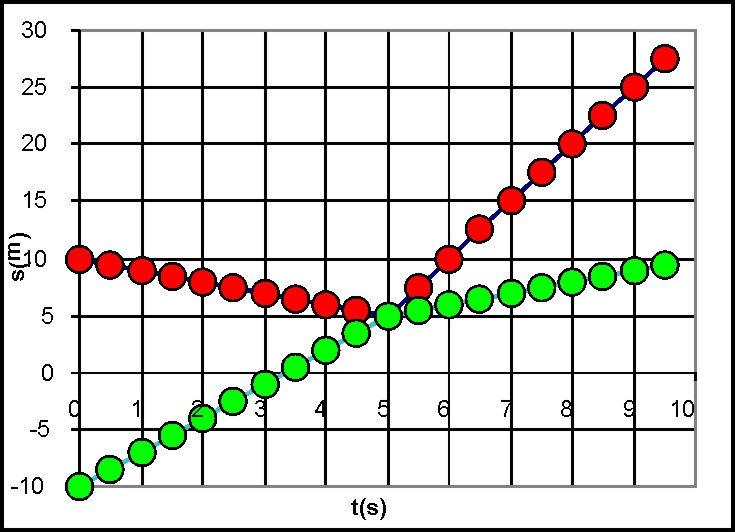
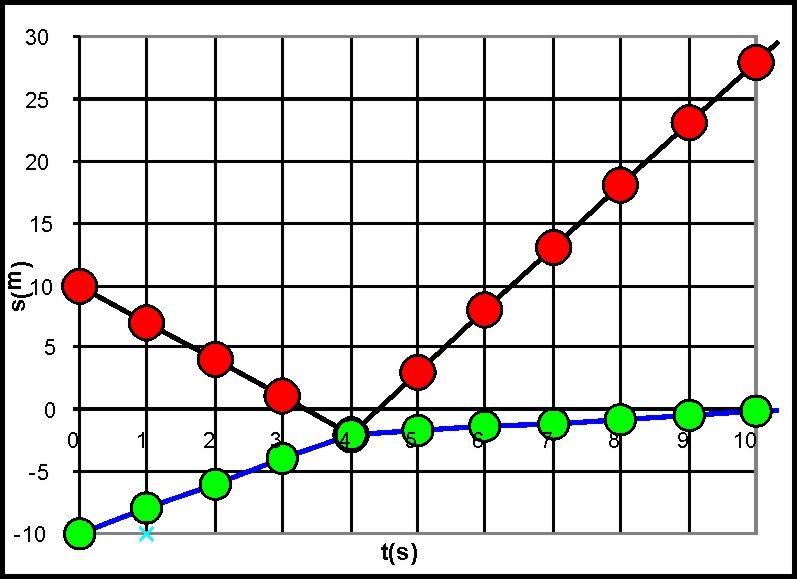
3.5.32. La gráfica de la figura corresponde a la representación del movimiento rectilíneo de dos cuerpos A (rojo en la gráfica) y B (verde en la gráfica), cuyas masas suman 4 kg, es una gráfica posición tiempo en un sistema de referencia de laboratorio, observándose que colisionan frontalmente en un instante determinado. Del análisis de dicha gráfica sacarás la conclusión que las velocidades respectivas antes de la colisión en un sistema de referencia del centro de masas serán:

a) 3 y -1 m/s

b) -3 y 1 m/s

c) 1 y -3 m/s

d) -1 y 3 m/s

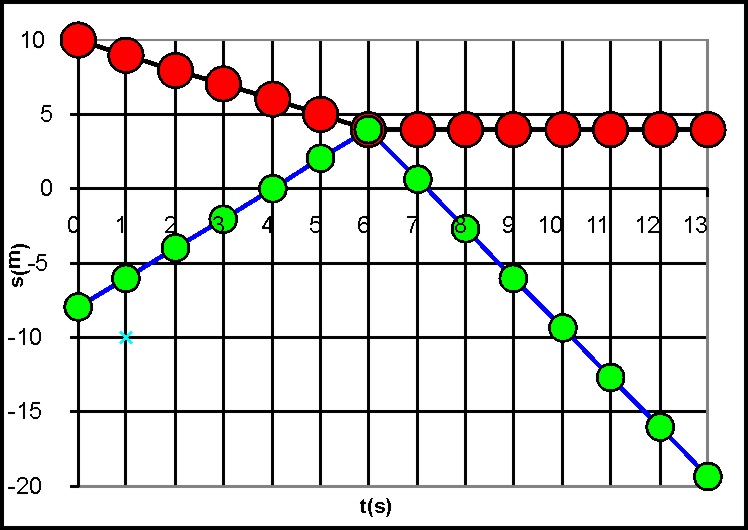
3.5.33.La gráfica posición/ tiempo de la figura corresponde a la representación del movimiento rectilíneo de dos cuerpos A(rojo) y B(verde), cuyas masas suman 6 kg, en un sistema de referencia de laboratorio, observándose que colisionan frontalmente a los 6s. Del análisis de dicha gráfica sacarás la conclusión que las velocidades respectivas después de la colisión en un sistema de referencia del centro de masas serán:

a) 2 y – 1 m/s

b) 0,5 y -2,5 m/s

c) 1 y -2 m/s

d) 2,5 y 0,5 m/s

3.5.34. La gráfica de la figura corresponde a la representación posición/tiempo del movimiento de dos cuerpos A y B, que se desplazan por el eje de las X y cuyas masas suman 10 kg, en un sistema de referencia de laboratorio, observándose que colisionan frontalmente a los 4s. Del análisis de dicha gráfica sacarás la conclusión que las velocidades respectivas después de la colisión en un sistema de referencia del centro de masas serán en m/s :

a) -4 y 1 b) 4 y -1

c) 1 y -4 d) -1 y 4

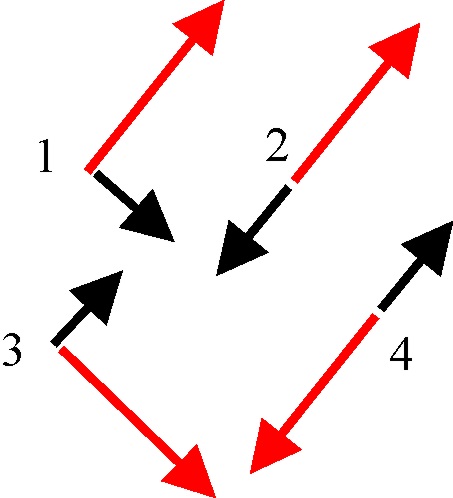
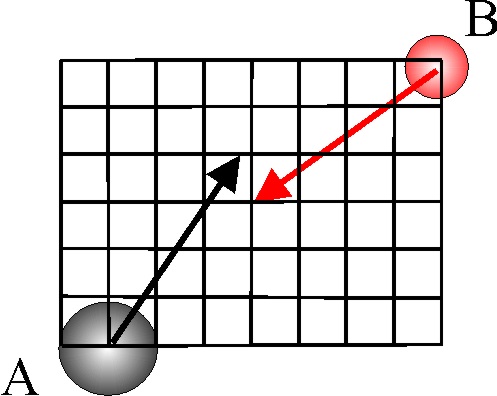
3.5.35. Dos cuerpos esféricos, A(rojo) y B(negro), de 4 y 6 kg de masa, respectivamente, se mueven en un movimiento rectilíneo y uniforme con velocidades de 6 y 8 m/s, en los sentidos indicados en dibujo, colisionando oblicua y elásticamente. Del estudio de su colisión en el sistema de referencia del centro de masas, dirás que sus velocidades respectivas en dicho sistema de referencia antes de la colisión están dadas en el esquema por los vectores:

a) 1

b) 2

c) 3

d) 4

Mientras que después de la colisión en el mismo sistema de referencia serán los vectores:

a) 1

b) 2

c) 3

d) 4

3.5.36. Dos cuerpos esféricos, A(negro) y B(rojo), de 10 y 5 kg de masa, respectivamente, se mueven en un movimiento rectilíneo y uniforme con velocidades de 5 y 5 m/s, indicadas en dibujo con sus vectores respectivos, colisionando oblicua y elásticamente. Cada cuadrado es una unidad del SI. Del estudio de su colisión en el sistema de referencia del centro de masas, dirás que sus velocidades respectivas en dicho sistema de referencia antes de la colisión están dadas en el esquema por los vectores:

a) 1

b) 2

c) 3

d) 4.

Mientras que después de la colisión en el mismo sistema de referencia serán los vectores:

a) 1

b) 2

c) 3

d) 4