ENSEÑANZA
DE LA FÍSICA Y LA QUÍMICA
1.7.MOVIMIENTO ARMÓNICO SIMPLE
1.7.1. La
gráfica elongación-tiempo de un movimiento vibratorio armónico (M.A.S.) tiene
la forma de la figura. Luego, la expresión de su velocidad será:
a)
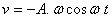
b)
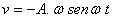
c)
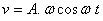
d)
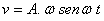
e)
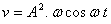
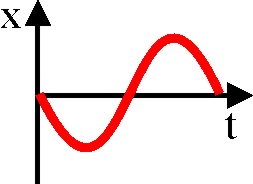
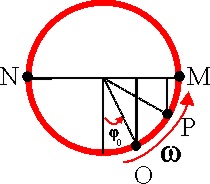
1.7.2.* Si
un punto material sale de M y llega a N según el esquema de la figura en un
tiempo t, recorriendo una semicircunferencia con movimiento uniforme, su proyección
sobre un diámetro MN describe un M.A.S. (movimiento armónico simple), representado
por una función cosenoidal cuya:
a) AMPLITUD ES EL RADIO
b) ACELERACIÓN ES 0
c) PERÍODO ES 4t SEGUNDOS
d) PULSACIÓN ES
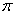 /t rads-1
/t rads-1
e) FASE INICIAL ES
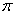 RADIANES
RADIANES
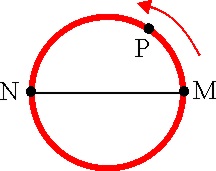
1.7.3*. Si
un punto material P que recorre la circunferencia según el esquema de la figura
se encuentra en el instante inicial en O, dirás que su proyección sobre el
diámetro MN realiza un M.A.S. representado por una función cosenoidal que
tiene:
a) UNA AMPLITUD IGUAL AL DIÁMETRO
b) UN PERÍODO QUE SERÁ EL TIEMPO QUE TARDA P EN
VOLVER A PASAR POR EL PUNTO O
c) UNA FASE INICIAL
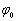
d) UNA ECUACIÓN DE MOVIMIENTO
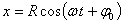
e) UNA ACELERACIÓN IGUAL A LA CENTRÍPETA MULTIPLICADA
POR
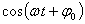
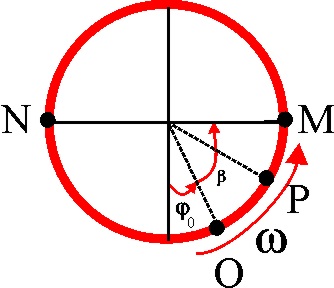
1.7.4.* Dado
el esquema de la figura en el cual un punto material P recorre la circunferencia
con módulo de su velocidad constante, partiendo inicialmente de O, podrás
decir que su proyección sobre el diámetro MN:
a) RECORRE DOS VECES LA DISTANCIA MN CUANDO P DA
UNA VUELTA COMPLETA
b) TIENE COMO FASE INICIAL EL ÁNGULO
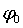
c) DA UNA OSCILACIÓN COMPLETA CUANDO VUELVE A PASAR
POR EL MISMO SITIO EN EL MISMO SENTIDO DE SU MOVIMIENTO
d) TIENE UNA PULSACIÓN QUE SERÁ IGUAL A 2
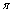 RADIANES DIVIDIDOS POR EL TIEMPO QUE TARDA EN DAR UNA OSCILACIÓN COMPLETA
RADIANES DIVIDIDOS POR EL TIEMPO QUE TARDA EN DAR UNA OSCILACIÓN COMPLETA
e) TIENE POR ECUACIÓN DEL MOVIMIENTO
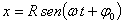
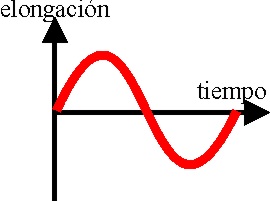
1.7.5. Un
móvil efectúa un movimiento vibratorio armónico (M.A.S.) cuya elongación frente
al tiempo está representada en la gráfica adjunta. La representación de la
aceleración (eje Y) frente al tiempo (eje X) será:
a)
A b) B c) C d) D
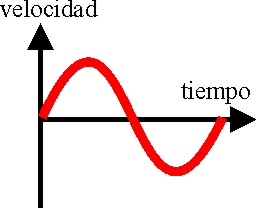
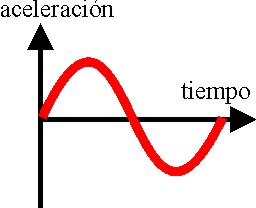
1.7.6. Un
móvil efectúa un movimiento vibratorio armónico, siendo la representación
de la velocidad frente al tiempo, la gráfica adjunta. La representación de
la aceleración (eje Y) frente al tiempo (eje X) será:
a) A b) B c)
C
d) D e) E
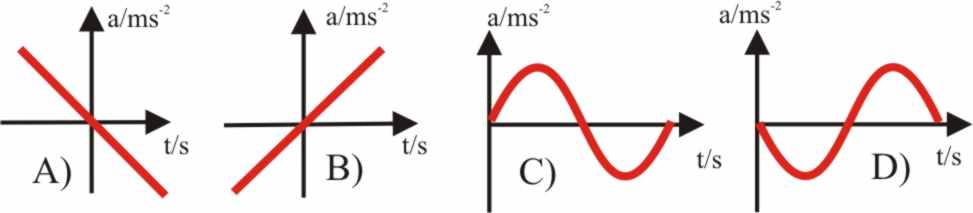
1.7.7. Un
móvil efectúa un movimiento vibratorio armónico (M.A.S.), siendo la representación
de la aceleración frente al tiempo, la gráfica adjunta. La representación
de la elongación (eje Y) frente al tiempo (eje X) será:
1.7.8. Un
móvil efectúa un movimiento vibratorio armónico (M.A.S.) sobre el eje AB,
siendo estos puntos sus posiciones extremas. Para la posición M del móvil:
a) SU VELOCIDAD ESTÁ SIEMPRE DIRIGIDA HACIA B
b) SU VELOCIDAD ES NULA
c) SU VELOCIDAD ESTÁ DIRIGIDA HACIA O
d) SU VELOCIDAD PUEDE ESTAR DIRIGIDA HACIA B O
HACIA O
e) SU VELOCIDAD,
EN MÓDULO, ES LA MÁXIMA QUE PUEDE TENER EL MÓVIL
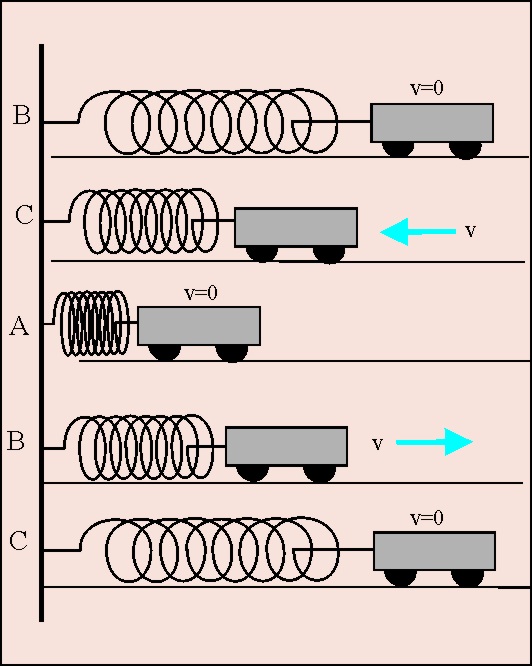
1.7.9. Un
móvil efectúa un movimiento vibratorio armónico simple (M.A.S.) sobre la línea
AB. En los cinco dibujos se representa el vector velocidad del móvil en distintas
posiciones. Sólo hay un dibujo correcto. Señálalo:
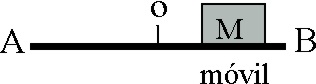

1.7.10.
Un
móvil efectúa un movimiento vibratorio armónico (M.A.S.) sobre el eje X. Cuando
t=0 el móvil tiene una elongación cero y cuando t=T/4 la elongación del móvil
es -A (siendo A la amplitud). Luego, la ecuación que describe este movimiento
es:
a)
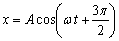 b)
b)
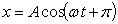
c)
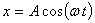 d)
d)
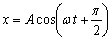
1.7.11. En
un movimiento vibratorio armónico la representación de la aceleración del
móvil (eje Y) frente a la elongación (eje X) es:

a)
A b) B c) C d)
D
e)
E
1.7.12.* Si
un punto material describe un M.A.S. recorriendo un diámetro, en las posiciones
en que invierte el sentido de su movimiento, dirás que:
a) SU VELOCIDAD ES 0
b) SU ACELERACIÓN ES 0
c) SU VELOCIDAD ES MÁXIMA
d) SU ACELERACIÓN CAMBIA DE SENTIDO
e) SU ACELERACIÓN ES MÁXIMA
1.7.13.* Si
te dicen que un punto material se mueve describiendo una trayectoria circular
de forma que el módulo de su velocidad se conserva constante, asegurarás que
su proyección sobre un diámetro cualquiera de dicha circunferencia realizará
un movimiento:
a) UNIFORME
b) UNIFORMEMENTE ACELERADO
c) CON ACELERACIÓN
QUE DEPENDE DE LA DISTANCIA AL CENTRO DE LA CIRCUNFERENCIA
d) CON ACELERACIÓN
CUYO SENTIDO VECTORIAL ES CONTRARIO AL DE SU VELOCIDAD SALVO EN SUS EXTREMOS
e) ARMÓNICO SIMPLE
1.7.14.* Si
estudias con detenimiento el movimiento armónico simple podrás asegurar que:
a) LA ELONGACIÓN ES LA SEPARACIÓN INSTANTÁNEA A
SU POSICIÓN DE ORIGEN O DE EQUILIBRIO
b) LA AMPLITUD ES LA SEPARACIÓN MÁXIMA DE SU POSICIÓN
A LA DE ORIGEN O DE EQUILIBRIO
c) LA FRECUENCIA DE DICHO MOVIMIENTO ES EL NÚMERO
DE VECES POR SEGUNDO QUE RECORRE EL DIÁMETRO
d) EL PERÍODO ES EL TIEMPO QUE TARDA EN RECORRER
UN DIÁMETRO
1.7.15. Si
un punto material que sale de P según el esquema de la figura recorre la circunferencia
de radio R con velocidad angular constante, y tarda un tiempo t en llegar
a P', su proyección sobre el diámetro MN, tendrá por ecuación de movimiento:
a)
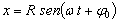 b)
b)
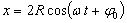
c)
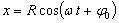 d)
d)
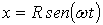
e)
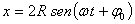
1.7.16. Un
movimiento vibratorio armónico está representado por la ecuación
x = A· sen(2
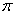 /T)t, luego su velocidad vendrá expresada por:
/T)t, luego su velocidad vendrá expresada por:
a)
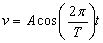 b)
b)
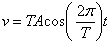
c)
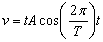 d)
d)
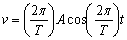
e)
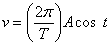
1.7.17. La
velocidad con que se desplaza la proyección de un punto material que recorre
la circunferencia con velocidad angular constante depende únicamente:
a) DEL RADIO
b) DEL ÁNGULO RECORRIDO Y DE LA AMPLITUD
c) DEL TIEMPO, VELOCIDAD ANGULAR O PULSACIÓN Y DEL
RADIO
d) DE LA ELONGACIÓN,
DEL RADIO Y DE LA VELOCIDAD ANGULAR
e) DE LA ELONGACIÓN Y DE LA VELOCIDAD LINEAL
1.7.18.* El
conocimiento de lo que es un M.A.S te permitirá asegurar que:
a) LA ELONGACIÓN DE DICHO MOVIMIENTO VENDRÁ DADA
POR UNA ECUACIÓN EN FUNCIÓN DEL COSENO O DEL SENO DEL ÁNGULO RECORRIDO SEGÚN
EL PUNTO DE ORIGEN DEL MOVIMIENTO O DEL DIÁMETRO O EJE QUE SE TOME COMO REFE-RENCIA
b) SU AMPLITUD SERÁ EL RADIO O EL DIÁMETRO SEGÚN
EL PUNTO DE REFERENCIA DE SALIDA DEL MOVIMIENTO CIRCULAR UNIFORME DEL QUE
EL M.A.S RESULTA PROYECCIÓN
c) LA AMPLITUD SI LA PROYECCIÓN PARTE DEL CENTRO
NUNCA SUPERARÁ EL RADIO
d) LOS ÁNGULOS RECORRIDOS SIEMPRE SE MEDIRÁN EN
RADIANES
e) SU FRECUENCIA ES EL NÚMERO DE VECES QUE LA PROYECCIÓN
RECORRE EL DIÁMETRO EN UN SEGUNDO
1.7.19. Si
comparas el M.A.S que realiza un cuerpo suspendido de un resorte con un hipotético
movimiento circular uniforme que en el mismo tiempo podría realizar un punto
P del mismo tal como se muestra en el esquema, te darás cuenta de que:
a) CUANDO RECORRE
UNA SEMICIRCUNFERENCIA LA VELOCIDAD DEL M.A.S CAMBIA DE SENTIDO
b) LA FUERZA QUE EJERCE EL RESORTE TIENE EL MISMO
SENTIDO QUE EL DESPLAZAMIENTO
c) LA FASE INICIAL DEL MOVIMIENTO ES
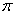 /2 RADIA-NES
/2 RADIA-NES
d) EL DESPLAZAMIENTO Y LA VELOCIDAD ESTÁN DESFASADOS
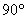
e) LA AMPLITUD DEL MOVIMIENTO ES EL DIÁMETRO
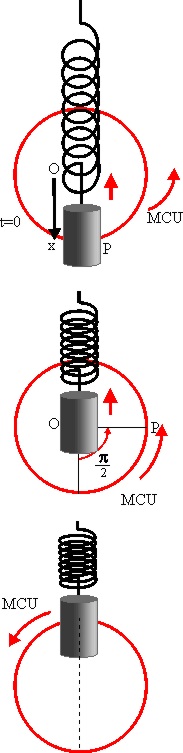
1.7.20.* Los
gráficos dados en los cuales se estudia la variación de una magnitud z con
el tiempo, en un M.A.S que corresponde a la proyección de un punto que saliendo
de la posición indicada recorre la circunferencia con un M.C.U. De ellos dirás
que z corresponderá a:
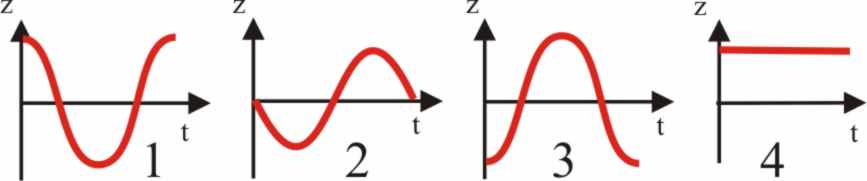
a) ELONGACIÓN
EN 1 b) ACELERACIÓN EN 3
c) VELOCIDAD
EN 2 d) VELOCIDAD ANGULAR EN 4
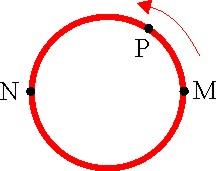
1.7.21. Si
estiras un muelle que mantiene un carrito sobre una mesa sin rozamiento y
llegado a una determinada posición, lo sueltas tal como muestra el esquema
de la figura, el vector velocidad con que se mueve dicho cuerpo variará con
la posición x y con el tiempo. De todos los gráficos dados, el que mejor representa
dicha variación será el:
a) a b) b c)
c
d) d e) NINGUNO DE LOS
DADOS
1.7.22. Dada
la ecuación del movimiento que realiza una masa colgada de un resorte previo
impulso inicial, y en el SI:
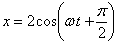
la gráfica que
mejor corresponde a la descripción de dicho movimiento es de las dadas es
la:
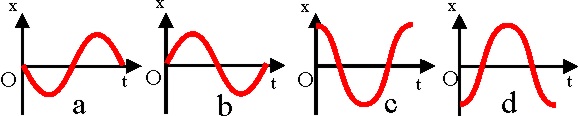
a) a b) b c) c
d) d
e) NINGUNA DE LAS DADAS
1.7.23.* Dada
la ecuación de un M.A.S, en el SI,
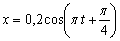 podrás decir que:
podrás decir que:
a) LA AMPLITUD DE DICHO MOVIMIENTO ES 0,2
b) EL PERÍODO SERA DE 0,5 SEGUNDOS
c) EL ÁNGULO DE FASE ES DE
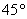
d) LA ELONGACIÓN SERA 0, UN CUARTO DE SEGUNDO DESPUÉS
DE COMENZAR EL MOVIMIENTO
e) SU VELOCIDAD MÁXIMA VALDRÍA
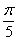 m/s
m/s
1.7.24.* Si
te dicen que un punto material de 2 kg realiza un M.A.S de 0,1m de amplitud
y que en un punto cuya elongación es de 0,05m su velocidad es de 4,35cm/s,
podrás asegurar que:
a) LA FRECUENCIA ES DE
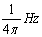
b) SU PULSACIÓN ES DE 0,5 rad/s
c) SU ECUACIÓN HORARIA ES
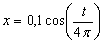
d) SU VELOCIDAD MÁXIMA ES DE 0,1 m/s
e) SU MÁXIMA ACELERACIÓN ES DE 0,025 m/s2
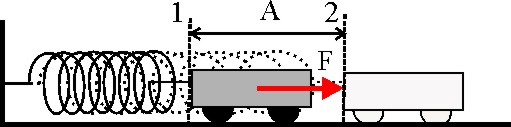
1.7.25. Si
en el esquema de la figura, aplicando la fuerza F desplazas el carrito unido
al resorte de la posición 1 a la 2, y luego lo sueltas sobre la mesa sin rozamiento,
dirás que:
a)
EL BLOQUE DESCRIBIRÁ UN MOVIMIENTO PERIÓDICO
b)
LA AMPLITUD DE DICHO MOVIMIENTO ES A
c)
TENDRÁ EL MÍNIMO DE VELOCIDAD EN LA POSICIÓN 2
d)
AL PASAR POR 1, TENDRÁ SU MÁXIMO DE VELOCIDAD
e)
PARARÁ AL VOLVER A PASAR POR 1
1.7.26.* Si
el bloque de la figura que está sobre una mesa sin rozamiento, unido a un
resorte se lleva de la posición 2 a la 3 y se suelta, realiza un movimiento
armónico simple, cuyas características vienen dadas por los gráficos A, B
y C de la figura. De ellos podrás decir que:

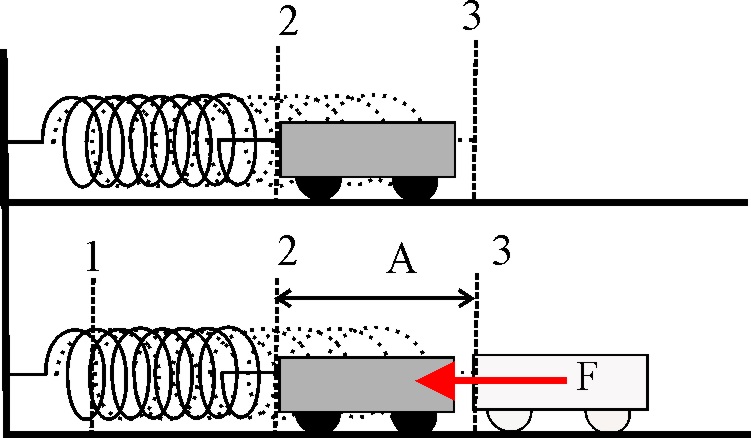
a) EL A REPRESENTA LA VARIACIÓN DE SU VELOCIDAD
CON EL TIEMPO
b) EL B REPRESENTA LA VARIACIÓN DE SU POSICIÓN CON
EL TIEMPO
c) EL C REPRESENTA LA VARIACIÓN DE SU ACELERACIÓN
CON EL TIEMPO
d) EL B CORRESPONDE A LA VARIACIÓN DE SU VELOCIDAD
CON EL TIEMPO
e) EL A CORRESPONDE A LA VARIACIÓN DE SU POSICIÓN
CON EL TIEMPO
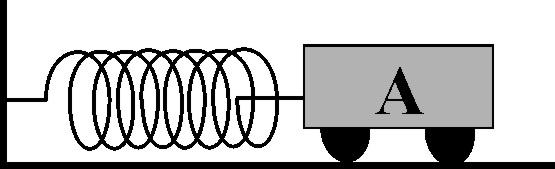
1.7.27. Si
el cuerpo A oscila con un M.A.S, sin
rozamiento con el suelo, una vez que se desplaza hacia la derecha una distancia
x, tal como se observa en la figura, la variación de su velocidad con su posición
x sobre el suelo vendrá dada por la gráfica:
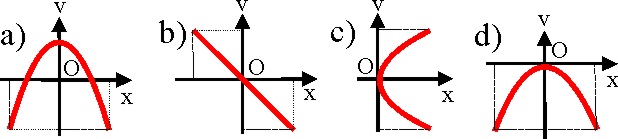
a) a b) b
c) c
d) d
e) NINGUNA DE LAS DADAS
1.7.28.* Un
resorte de 8cm se alarga hasta 12 cm cuando se le cuelga una masa de 200g.
Si después ejerces un ligero tirón hacia abajo sobre dicha masa, hasta que
el resorte alcance una longitud de 14 cm, y la sueltas,
dirás que:
a) LA MASA EFECTÚA UN M.U.A
b) LA MASA EFECTÚA UN MOVIMIENTO PERIÓDICO
c) LA MASA EFECTÚA UN M.A.S DE AMPLITUD 2cm
d) EL TIEMPO QUE TARDA EN SUBIR Y VOLVER A BAJAR
ES DE CASI 0,4s.
1.7.29.* Si
un cuerpo de 1 kg que oscila de un muelle de forma que su movimiento sea registrado
por un puntero pegado a él, en una cinta de papel que se mueve horizontalmente
con una velocidad de 0,1m/s tal como indica la figura, dirás que:
a) LA FRECUENCIA DE SU OSCILACIÓN ES DE 0,2 vueltas/s
b) LA LONGITUD DE ONDA REGISTRADA ES DE 0,75m
c) LA AMPLITUD MÁXIMA DEL MOVIMIENTO ES DE 0,1m
d) LA ECUACIÓN DEL M.A.S DESARROLLADA ES
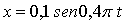
1.7.30. Cuando
se combinan 2 movimientos armónicos simples hay que tener muy en cuenta la
diferencia de fase entre ellos, amplitudes y frecuencias, y en el caso de
que las dos primeras magnitudes sean iguales, como en el caso de y1=3·sen2t
e y2=3·sent, la función y, que asocia a las dos tiene una:
a) AMPLITUD QUE DEPENDE DEL TIEMPO
b) AMPLITUD CONSTANTE IGUAL A 6
c) ELONGACIÓN MÁXIMA PARA t=0
d) FRECUENCIA IGUAL A
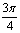
e) AMPLITUD IGUAL A 3
1.7.31.* Si
dos movimientos armónicos simples están desfasados entre si
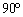 , pero tienen igual frecuencia, su combinación produce una serie de figuras
muy interesantes denominadas de Lissajous, matemático francés que las investigó
en 1857. Así, si se trata de obtener el movimiento resultante de
, pero tienen igual frecuencia, su combinación produce una serie de figuras
muy interesantes denominadas de Lissajous, matemático francés que las investigó
en 1857. Así, si se trata de obtener el movimiento resultante de
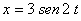 e
e
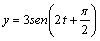 , podrías decir que:
, podrías decir que:
a) EL VECTOR DE POSICIÓN
RESULTANTE SERÍA
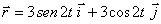
b) LA AMPLITUD RESULTANTE SERÍA SIEMPRE 3
c) LA ECUACIÓN DE LA TRAYECTORIA ES UNA CIRCUNFERENCIA
DE RADIO 3
d) LA FRECUENCIA DEL MOVIMIENTO SERÍA CONSTANTE
E IGUAL A 1/
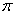
1.7.32.* La
resultante de los movimientos armónicos dados por las ecuaciones
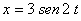 e
e
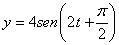 tiene:
tiene:
a) UN VECTOR DE POSICIÓN
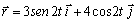
b) UNA ECUACIÓN DE TRAYECTORIA QUE ES UNA CIRCUNFERENCIA
DE RADIO IGUAL A 5
c) UNA ECUACIÓN DE TRAYECTORIA QUE ES UNA ELIPSE
DE SEMIEJES 3 Y 4
d) UNA AMPLITUD RESULTANTE CONSTANTE IGUAL A 5
e) UN PERÍODO IGUAL A
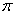 SEGUNDOS
SEGUNDOS
1.7.33. La
ecuación de la trayectoria resultante de la combinación de dos movimientos
armónicos simples perpendiculares, de igual frecuencia y amplitud, desfasados
en
 , sería una:
, sería una:
a) CIRCUNFERENCIA DE RADIO IGUAL A LA AMPLITUD
b) ELIPSE
c) RECTA BISECTRIZ DE LOS EJES XY
d) RECTA DE ECUACIÓN y = -x
e) RECTA QUE CONTENDRIA A UN DIÁMETRO DE LA CIRCUNFERENCIA
DE RADIO IGUAL A LA AMPLITUD
a) A b) B c)
C
d) D d) NINGUNO DE LOS DADOS
![]()
![]()
![]()
![]()
![]()
![]() /t rads-1
/t rads-1![]() RADIANES
RADIANES![]()
![]()
![]()
![]()
![]() RADIANES DIVIDIDOS POR EL TIEMPO QUE TARDA EN DAR UNA OSCILACIÓN COMPLETA
RADIANES DIVIDIDOS POR EL TIEMPO QUE TARDA EN DAR UNA OSCILACIÓN COMPLETA![]()


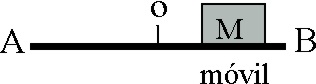







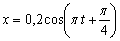
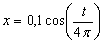





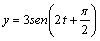 , podrías decir que:
, podrías decir que: