ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
TERMODINÁMICA 17. Transformaciones de estado
320.
El alumno de enseñanzas medias, asocia a Clapeyron,
ingeniero francés y profesor en Rusia, con la ecuación de los gases perfectos y
con el estudio de la vaporización de las sustancias, sin embargo lo que no
suele recordarse es que en 1834, introdujo los diagramas P/V, tan útiles para
estudiar las transformaciones de los sistemas termodinámicos. En él un proceso
isotérmico se representa por:
a)
Recta horizontal b)
Recta vertical
c)
Una parábola d)
Una hipérbola equilátera

324.
Un sistema evoluciona de un estado A, a otro B, observando los dibujos podrás
asegurar que para resolverlo tendrás que aplicar la fórmula:
a)
![]() b)
b)
![]()
c)
![]() d)
d)
![]()
325.
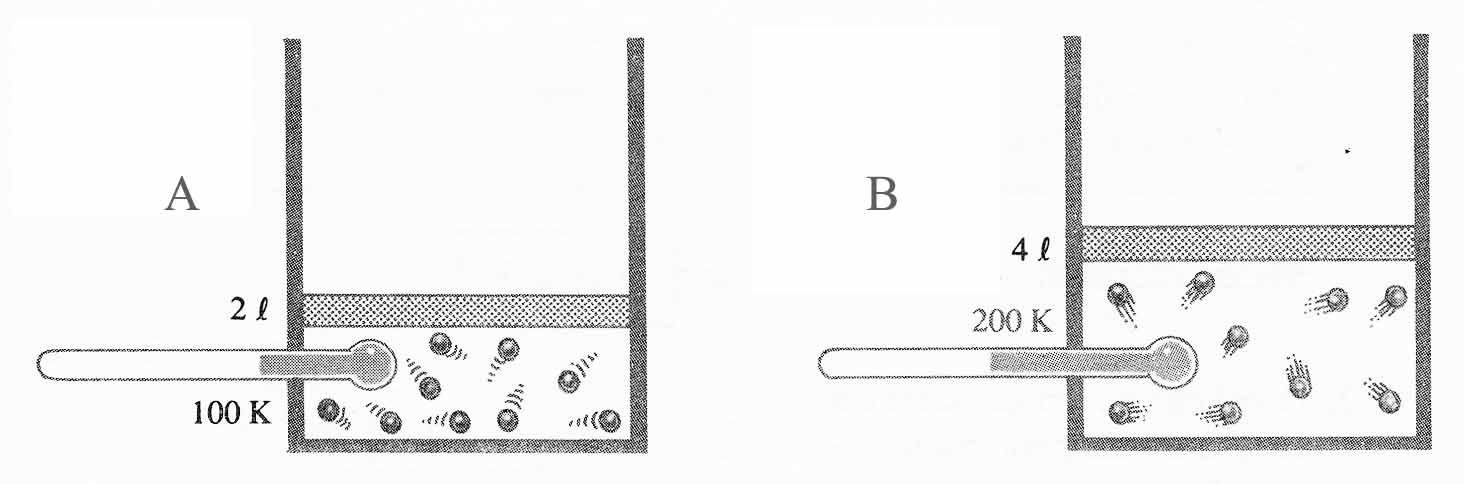
Un sistema evoluciona tal como se indica. Obser-vando los dibujos podrás asegurar que se trata de un proceso:
a) Isobárico b) Isocórico
c)Isotérmico d) Sin transferencia de energía
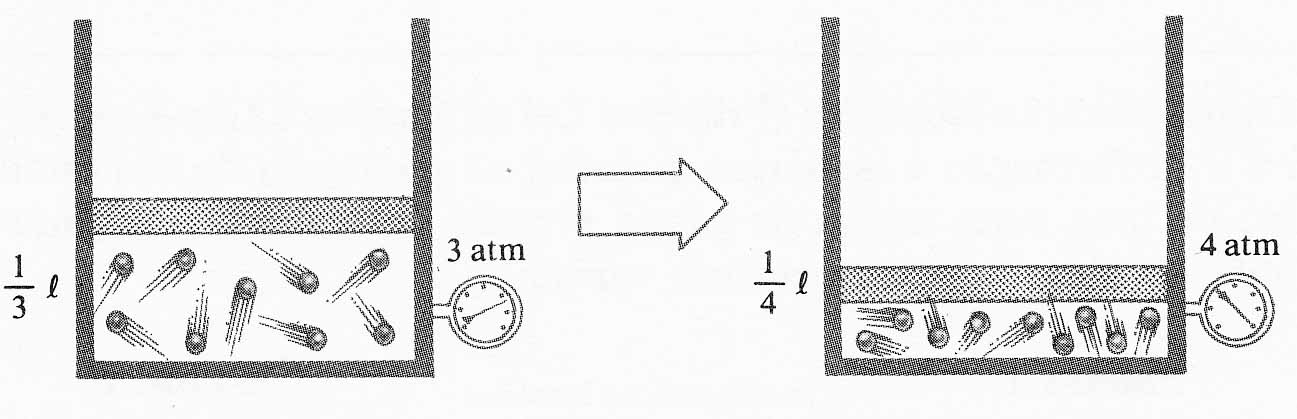
326.
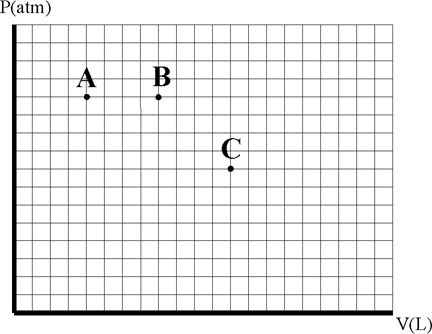
Los puntos A, B y C, representan tres estados de un mismo gas ideal, en un
diagrama PV, si comprendes las leyes de los gases dirás que:
a) TC >TB>TA
b) TA >TB>TC
c) TA <TB=TC
d) TA =TC <TB
327.
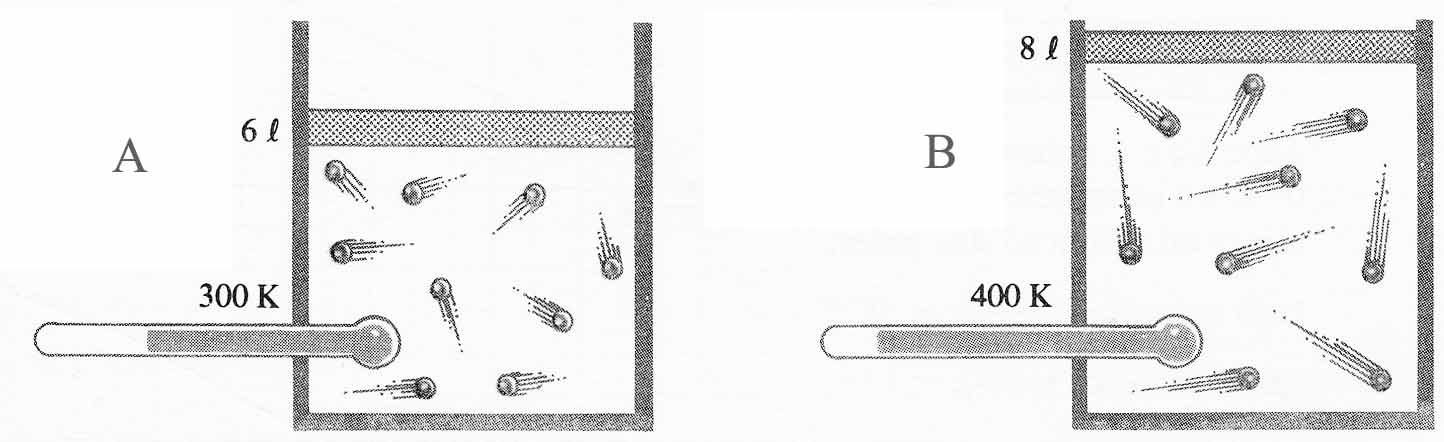
Un sistema evoluciona de A hasta B, tal como se indica. Observando los dibujos
podrás asegurar que se trata de un proceso:
a) Isobárico
b) Isocórico
c)Isotérmico
d)Sin transferencia de energía
328.
Un sistema evoluciona de A hasta B, tal como se indica. Observando los dibujos
podrás asegurar que se trata de un proceso:
a) Isobárico
b) Isocórico
c)Isotérmico
d) Sin transferencia de energía
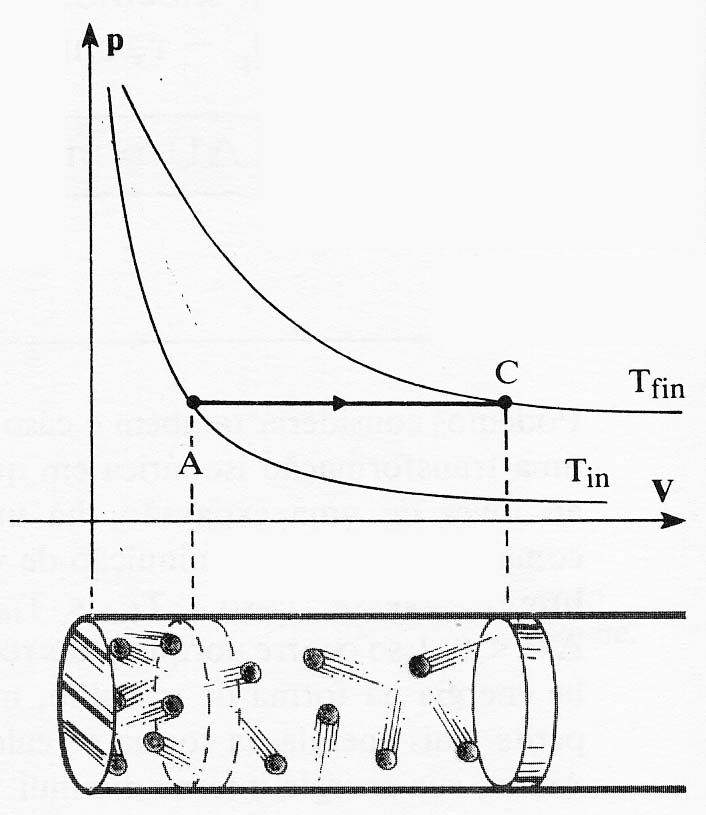
329*.
En el dibujo de la figura, se observa una transformación de un sistema gaseoso desde
A hasta C, situados en isotermas diferentes. Desde el punto de vista
microscópico podrás asegurar que:
a)El número de colisiones de las partículas del gas
aumentó
b)La velocidad de las partículas disminuyó
c)El número de colisiones de las partículas se
mantiene constante
d) La velocidad de las partículas aumentó

323.
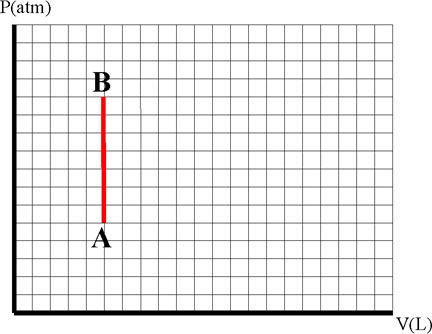
La línea que representa la evolución de un sistema desde un estado A, a otro B,
dada en el diagrama PV de la figura,
corresponde a un proceso:
a) Isobárico b) Isocórico
c) Isotérmico d)
Sin transferencia de energía
321.
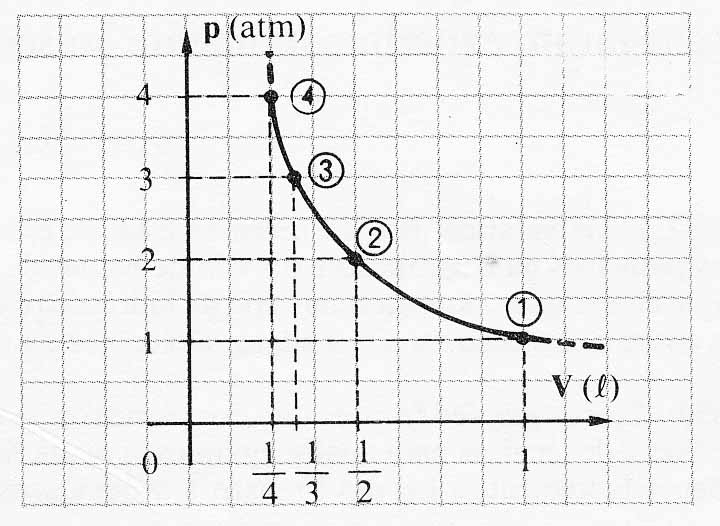
En el dibujo adjunto, observas que en los puntos 1,2,3 y 4 representados en la
curva, el producto de la presión por el volumen siempre es 1atm.L. Eso quiere
decir que estás representando una transformación:
a) Isobárica b)Isotérmica c)Isocórica d)Adiabática
322.
El prefijo iso, significa igual, y baros significa
pesado en griego, aunque se haya tomado siempre como presión. Coras, procede del griego y tal como el español corteza,
significa envoltura, por eso una ISOCORA mantiene igual la envoltura o sea el volumen, al igual que la ISOTERMA con la temperatura. En un
diagrama PV, una isobara estaría representada por una línea:
a) Recta horizontal b) Recta vertical
c) Una parábola d) Una hipérbola equilátera
331*.
En el dibujo de la figura, se observa una transformación de un sistema gaseoso.
Desde el punto de vista microscópico podrás asegurar que:
a)El número de colisiones de las partículas del gas
aumentó
b)La velocidad de las partículas disminuyó
c)El número de colisiones de las partículas se
mantiene constante
d) La velocidad de las partículas se mantienen
constante
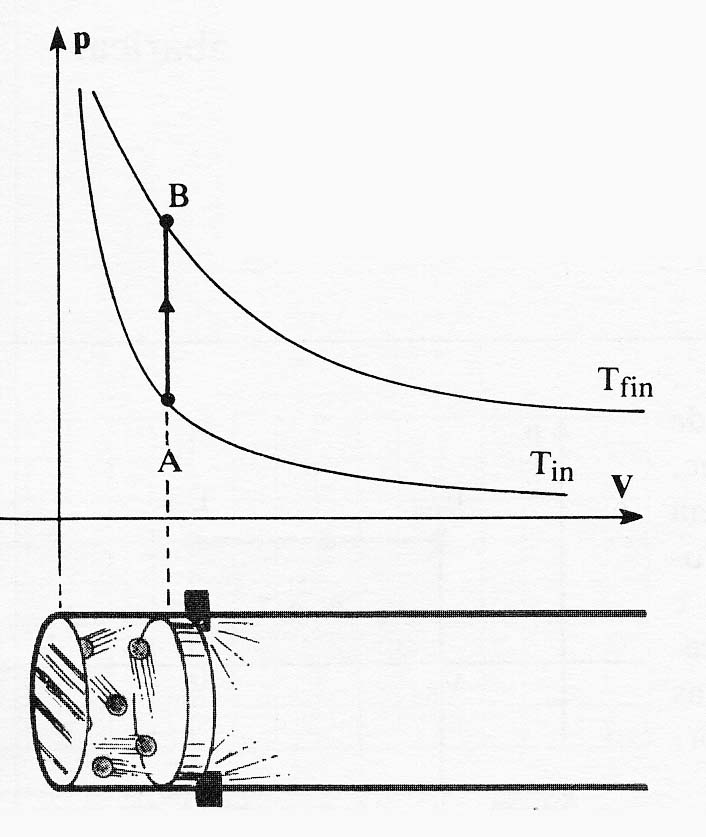
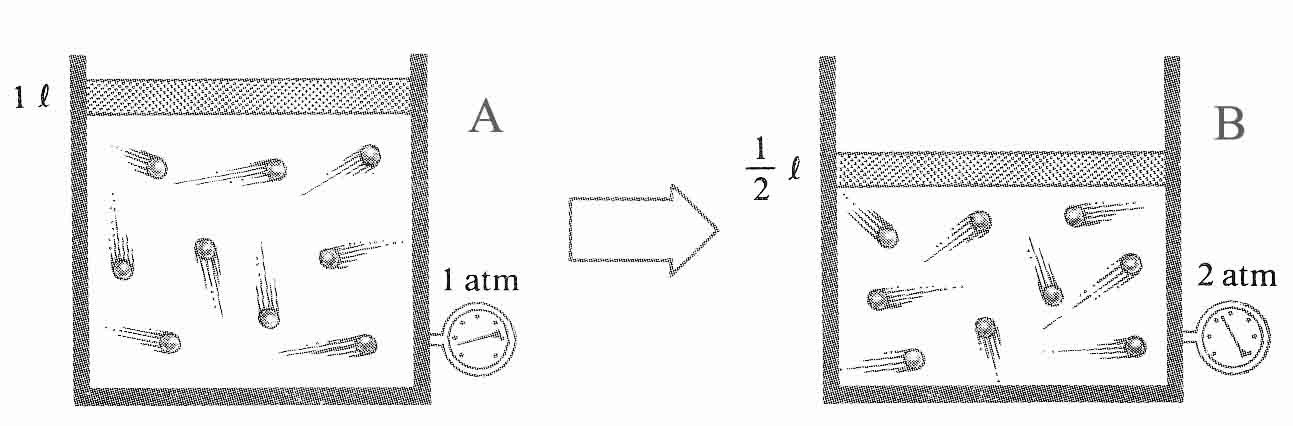
330*.
En el dibujo de la figura, se observa una transformación de un sistema gaseoso
desde A hasta B, situados en isotermas diferentes. Desde el punto de vista
microscópico podrás asegurar que:
a)El número de colisiones de las partículas del gas
aumentó
b)La velocidad de las partículas disminuyó
c)El número de colisiones de las partículas se
mantiene constante
d) La velocidad de las partículas aumentó
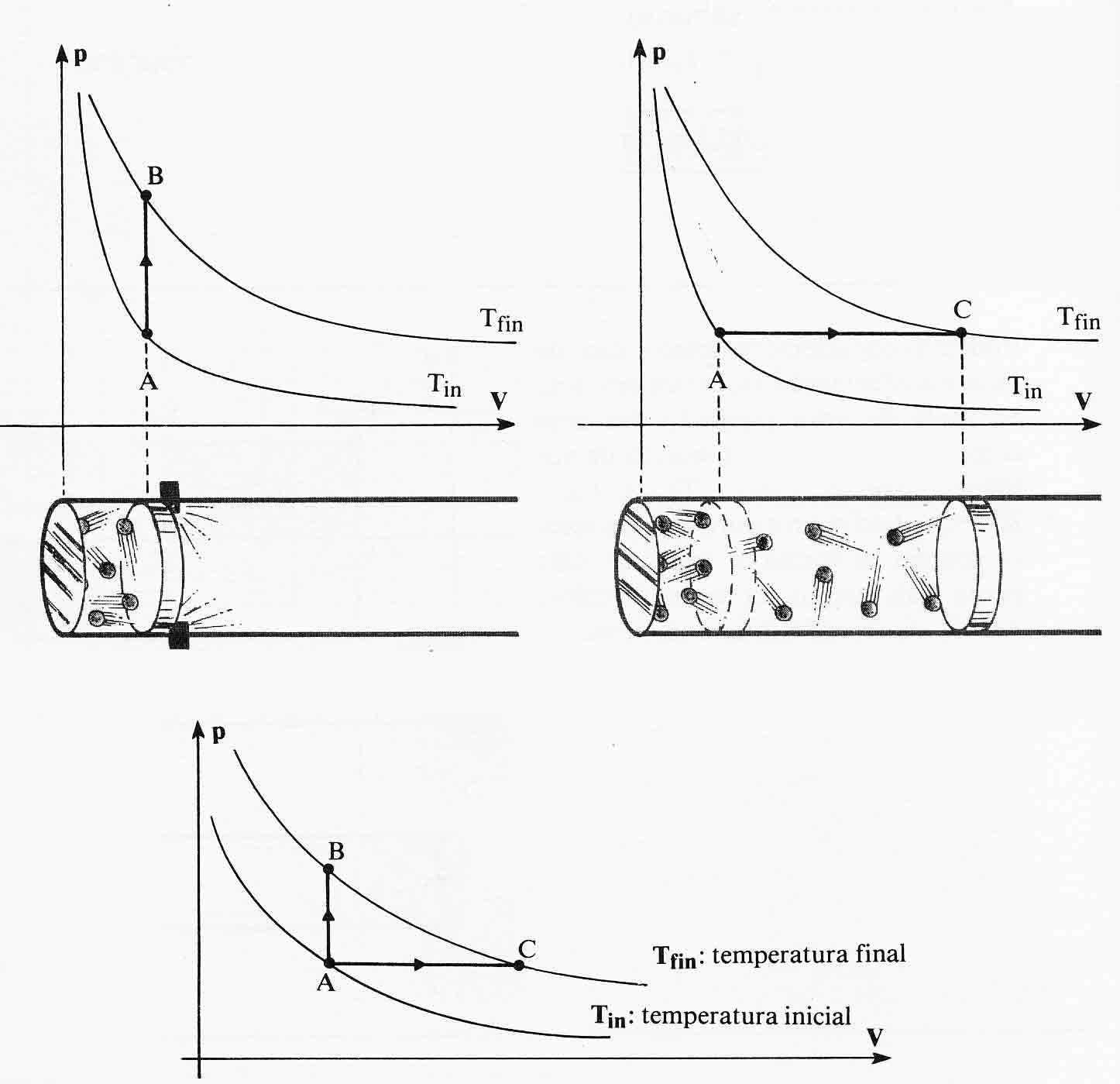
333*.
En el dibujo de la figura, se observan dos transformaciones de un sistema
gaseoso desde A hasta B, y desde A hasta C. Desde el punto de vista
microscópico podrás asegurar que en la primera, comparada con la segunda:
a)El número de colisiones de las partículas del gas
aumentó
b)La velocidad de las partículas disminuyó
c)El número de colisiones de las partículas se
mantuvo constante
d) La velocidad de las partículas aumentó
334*.
Se ha visto en los test anteriores lo que eran las variables de estado, especie
de coordenadas independientes, que permitían estudiar un sistema. Pues bien,
las funciones de estado son, como dice su nombre funciones dependientes de las
variables, pero que a su vez no dependen de cómo evoluciona el sistema, sino
solamente de su estado inicial o final. Dirás que serán funciones de estado:
a) La energía
interna de un sistema
b) El calor
intercambiado por un sistema
c) El trabajo
desarrollado por un sistema a presión constante
d) La variación
de entalpía de un sistema
332*.
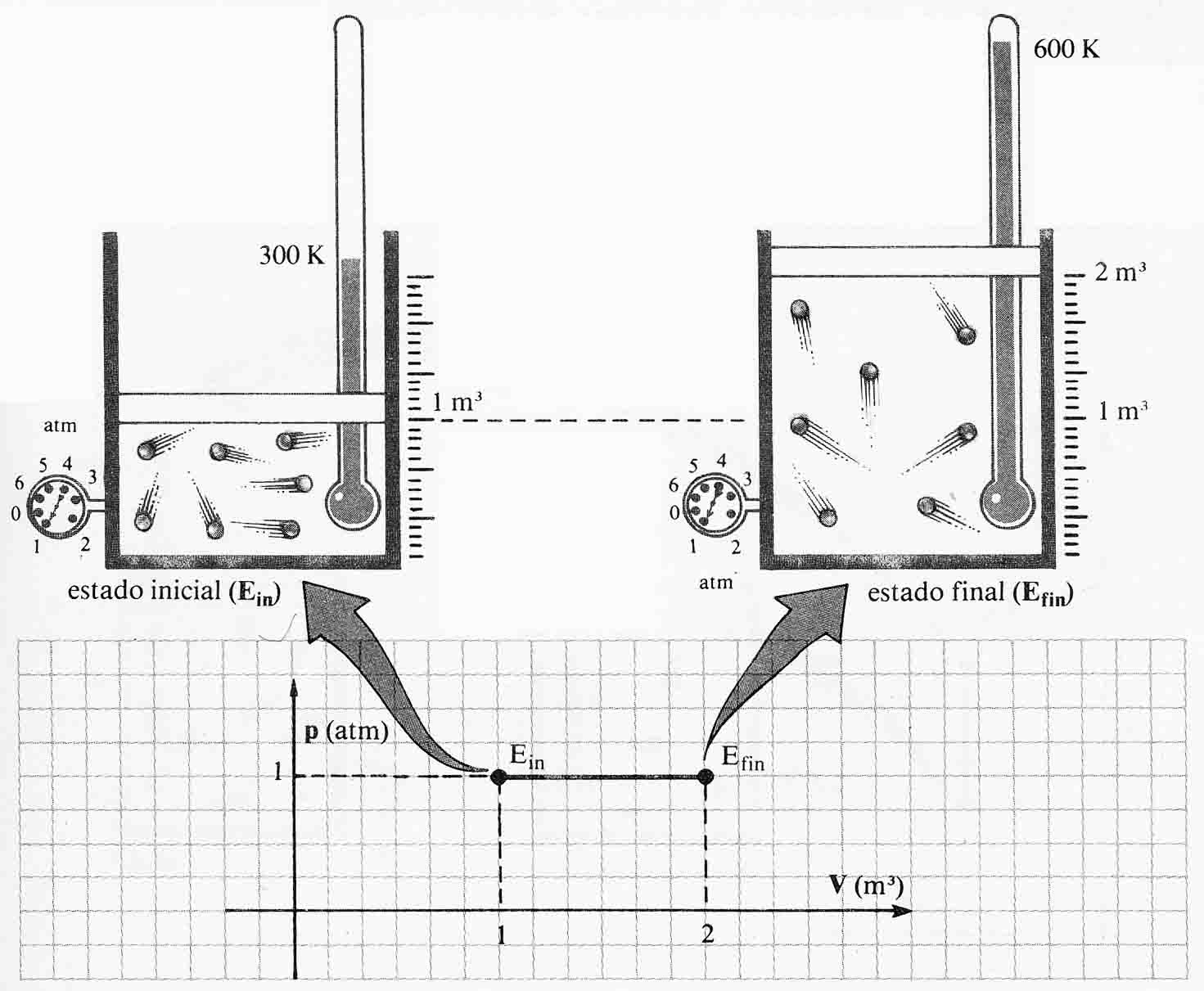
En el dibujo de la figura, se observa una transformación de un sistema gaseoso
desde un estado inicial hasta otro final. Desde el punto de vista microscópico
podrás asegurar que:
a)El número de colisiones de las partículas del gas
aumentó
b)La velocidad de las partículas disminuyó
c) El número de colisiones de las partículas se
mantiene constante
d) La velocidad de las partículas aumentó
338*.El término adiabático propuesto por Rankine, significa sin intercambio y los sistemas en estos
procesos no intercambian energía (como el caso de un termo), por lo que el
primer principio de termodinámica aplicado a un proceso de este tipo para un
mol de un gas, produciría que :
a) )U=W b) )U=
-W c) 0=W+Q d) CV =RT
339.
Los procesos isotérmicos, siempre se realizan muy lentamente mientras que los
adiabáticos para que no se produzca el intercambio, deberán hacerse muy
rápidamente. Las primeras expansiones adiabáticas fueron estudiadas, en la
colaboración entre Joule y el joven Thomson en 1847,
expansiones que daban lugar a un notable enfriamiento del sistema, y que serían
la base de los frigoríficos, y que justificarían las fuerzas de interacción y
las energías de enlace entre las moléculas de los gases Si este hecho lo representamos en una gráfica
PV, la ecuación indicada para ello sería:
a) PV=Cte b)
P= cte c)
V= cte. d) PV(=cte
340.
Si se pretende averiguar como evolucionan las variables de estado P,V y T en una
transformación isocórica de un sistema gaseoso ideal,
tendremos que emplear la ecuación:
a) P/T = constante b) PV= constante c) V/T= constante d) PV(=cte
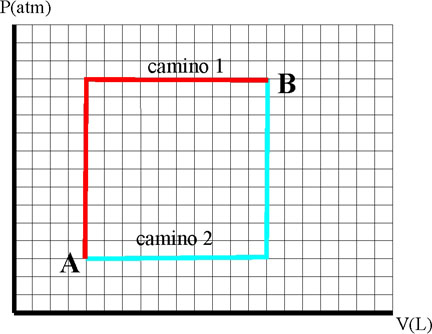
335*.El
trabajo se puede calcular fácilmente en un diagrama de Clapeyron,
dado que será la superficie abarcada en una gráfica PV, que expresa la
evolución de un sistema gaseoso que se comporta como un gas noble, por este
motivo si un sistema puede evolucionar desde A hasta B, por los dos caminos
dados en la gráfica, dirás que:
a) El trabajo no
es una función de estado
b) El trabajo es
independiente del camino seguido en la evolución
c) El trabajo
por en camino 1 es igual que por el
camino 2
d) El trabajo de A a B por cualquier camino siempre será <0
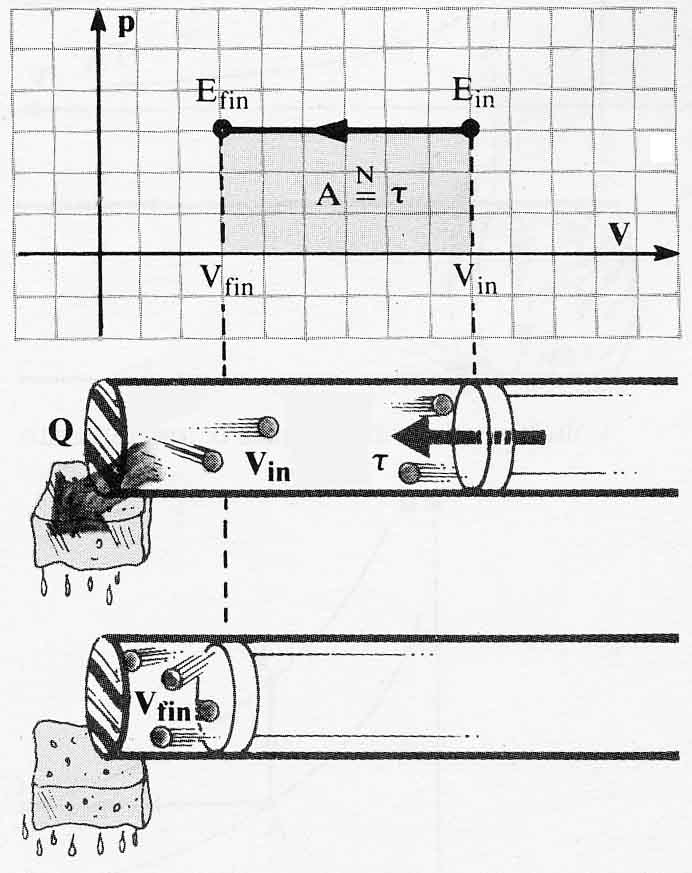
336*.
El sistema gaseoso de la figura se enfría desde un estado inicial, hasta otro
final, manteniendo la presión constante. El trabajo efectuado ↊, siempre
será:
a) positivo b)el área abarcada
en un diagrama PV
c) negativo d)
cero
mientras que la velocidad de las moléculas:
a) se mantiene constante b) aumenta
c)disminuye d)No
influye en ↊
337.Clausius,
en 1854, calcula el trabajo desarrollado por un sistema como el producto de la
presión que se ejerce, por la variación de volumen, por ese motivo si un
sistema gaseoso evoluciona como indica el dibujo del test anterior, la energía interna del sistema habrá:
a) aumentado b) disminuido
c) será igual al trabajo efectuado d) será igual al calor desprendido