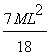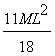ENSEÑANZA
DE LA FÍSICA Y LA QUÍMICA
4. SÓLIDO RÍGIDO
4.1. MOVIMIENTO DE UN SÓLIDO RÍGIDO. MOMENTO DE
INERCIA
4.2. FUERZAS Y MOMENTOS EN DINÁMICA DE ROTACIÓN
4.3. TRABAJO Y ENERGÍA DEL SÓLIDO EN ROTACIÓN.
CONSERVACIÓN.
4.4. CONSERVACIÓN DEL MOMENTO ANGULAR
4.1. MOVIMIENTO
DE UN SÓLIDO RÍGIDO. MOMENTO DE INERCIA. DETERMINACIÓN.
4.1.1*. Un sólido rígido es
como un:
a)
SISTEMA DE INFINITOS PUNTOS MATERIALES CUYO CENTRO
DE MASAS NO CAMBIA DE POSICIÓN RESPECTO DE UNOS EJES FIJADOS EN EL CUERPO.
b)
SISTEMA DE INFINITOS PUNTOS MATERIALES CUYA DISTANCIA
ENTRE ELLOS SE MANTIENE CONSTANTE AUNQUE SE MUEVA
c)
SISTEMA DE PUNTOS MATERIALES TALES QUE AL SUMAR
LA MASA DE TODOS, SE
OBTIENE LA MASA DEL CUERPO.
d)
PUNTO MATERIAL DE GRAN MASA
4.1.2. * Todos los puntos de
un sólido rígido que gira alrededor de un eje, independiente de su distancia
a éste, tienen la misma:
a) ACELERACIÓN
ANGULAR
b) VELOCIDAD LINEAL
c) VELOCIDAD
ANGULAR
d) DESPLAZAMIENTO
ANGULAR
4.1.3. Cuando
un cilindro rígido de radio R, rueda por una mesa (rueda sin deslizar),en
cada instante:
a)
TODOS LOS PUNTOS QUE ESTÁN EN CONTACTO CON EL
SUELO TIENEN
VELOCIDAD NULA
b)
LOS QUE ESTÁN A UNA DISTANCIA 2R DEL SUELO, TIENEN
UNA VELOCIDAD
DOBLE QUE LA DEL CENTRO DE MASAS.
c)
LA VELOCIDAD DEL CENTRO DE
MASAS ES SOLO DE TRASLACIÓN
d)
CUALQUIER PUNTO SITUADO RESPECTO DEL CENTRO DE
MASAS A UNA DISTANCIA INFERIOR AL RADIO R, TIENE UNA VELOCIDAD MAYOR QUE EL
DOBLE DE LA DEL CENTRO DE MASAS.
4.1.4.* El momento de inercia
de un sólido respecto a un eje que pasa por su centro de gravedad:
a)
ES UNA MAGNITUD
VECTORIAL
b)
MIDE LA INERCIA
DE UNA MASA EN ROTACIÓN
c)
SE MIDE EN
EL SI. EN kg.m
d)
ES IGUAL
A LA MASA DEL CUERPO POR SU RADIO DE GIRO AL CUADRADO
e)
DEPENDE DEL
EJE SOBRE EL QUE GIRE EL CUERPO
4.1.5. Euler,
en 1760, escribe la "Theoría motus corporum solidorum", en ella
se fijan las bases de la mecánica del cuerpo sólido y se define el momento
de inercia. Para calcularlo de forma simplificada es necesario determinar
el radio de giro. Si dispones de una pieza formada por tres cilindros coaxiales
de igual masa M y cuyos radios extremos son iguales y dobles del de la pieza
central R, dirás que su radio de giro al rodar sobre una mesa es:
a)
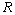 b)
b)
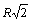 c)
c)
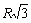 d)
d)

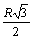
I. de un cilindro respecto
de un eje que pasa por su c.d.m.= mr˛/2
4.1.6. Cuatro
esferitas de masas m1=1g, m2=2g,
m3=3g y m4=4g están engarzadas mediante un alambre de masa
despreciable y longitud L=0,9m. Las masas m1 y m4 ocupan
los extremos del alambre y m2 está a una distancia L/4 de m1,
mientras que m3 está a la misma distancia de m4. Si
al sistema se le dota de un eje que pase por el centro de masas y sea perpendicular
al alambre resulta que el momento de inercia, expresado en kg.m2,
es:
a) 10-2 b) 10-3 c) 10-4 d) 10-5
en cambio
si el eje de giro pasase justamente por la bola m1 el valor del
momento de inercia en las mismas unidades es:
a) 4,7.10-2 b) 4,7.10-3 c) 4,7.10-4 d) 3,3.10-5
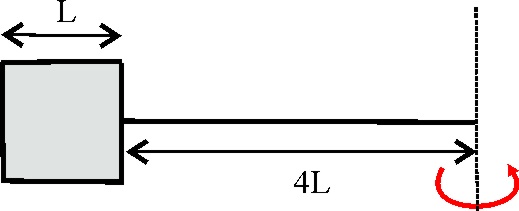
4.1.7. Una
pala matamoscas está hecha con cuatro varillas metálicas de masa M y longitud
L, que tensan una tela metálica de masa despreciable, soldadas por el centro
de una varilla a un mango de longitud 4L, y de masa M. Si para matar una mosca
la haces girar desde su extremo, su momento de inercia será aproximadamente:
a) 84 ML2 b) 80ML2
c) 90ML2
d) 87 ML2
Momento de
Inercia de una varilla de masa m y longitud L, respecto a un eje que pasa
por su c.d.m I0= mL˛/12
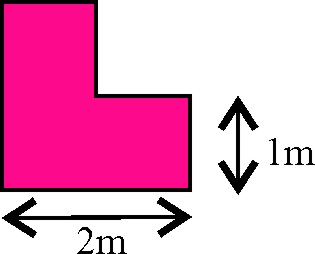
4.1.11. Una
superficie plana tiene la forma y dimensiones indicadas en la figura. Si existe
un eje de rotación que pasa por el centro de masas y es perpendicular a ella,
el momento de inercia es:
a) 2m/9
b) 3m/9
c) 4m/9 d) 5m/9
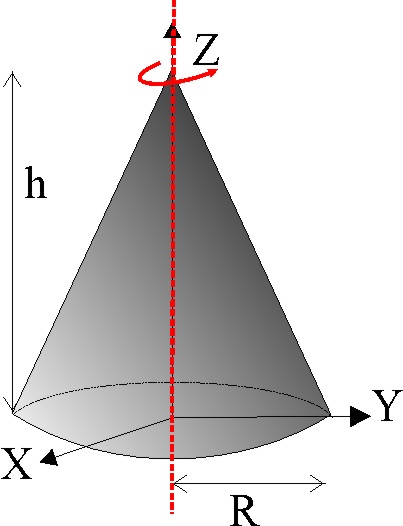
4.1.12. El
momento de inercia de un cono de radio de la base R y altura h respecto a
un eje que pasa por su vértice y por el centro de la base es:
a)
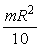 b)
b)
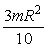
c)
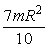 d) mR2
d) mR2
4.1.13. Si
un sólido rígido tiene el mismo momento de inercia respecto a los tres ejes
cartesianos que pasan por el centro de masas, podrás asegurar que este cuerpo
es:
a) UNA ESFERA MACIZA
b) UN CILINDRO MACIZO
c) UNA CORTEZA ESFÉRICA
d) UN ARO
e) NO SE
PUEDE PRECISAR
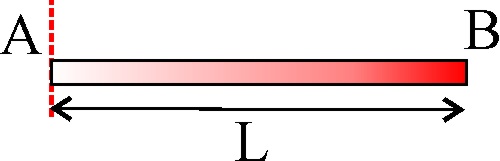
4.1.14. Una
varilla delgada tiene una masa M y una longitud L. La densidad crece uniformemente
desde un extremo A hasta el otro B de tal modo que la densidad en el extremo
B es doble que en el A. Si la varilla posee un eje perpendicular a la misma
y que pasa por el extremo A, el momento de inercia respecto a ese eje, vale:
a)
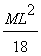 b)
b)
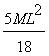
c)
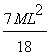 d)
d)
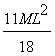
4.1.15. Una
varilla delgada tiene una masa M y una longitud L. La densidad crece de forma directamente proporcional
a su longitud desde un extremo A hasta el otro B. Si la varilla posee un eje
perpendicular a la misma y que pasa por el extremo A, el momento de inercia
respecto a ese eje, vale:
a)
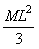 b)
b)
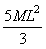
c)
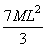 d)
d)
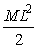
4.1.16. Un
cilindro A, un cilindro hueco (corteza) B, una esfera C, un aro D, y una esfera
hueca (corteza) E, de la misma masa m y radio R, pero diferente material,
se hacen rodar por una mesa. Sus momentos de inercia respectivos estarán ordenados
así:
a) A=B=C=D=E b) D>B>E>C>A
c) D=B=E>A>C
d) D=B>E>A>C
Datos:
Momento de inércia de una esfera hueca=
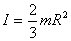
Momento de inércia de una esfera maciza =
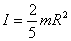
4.1.17. Si
un cilindro de masa M y radio R, lo atraviesas por un diámetro en el punto
medio de su altura H, con un alambre rígido que sostienes por sus extremos
y la hacer girar el momento de inercia en ese caso será:
a) MR2/2
b) MR2/4
c) DEPENDERÁ
DE LA ALTURA d) MR2

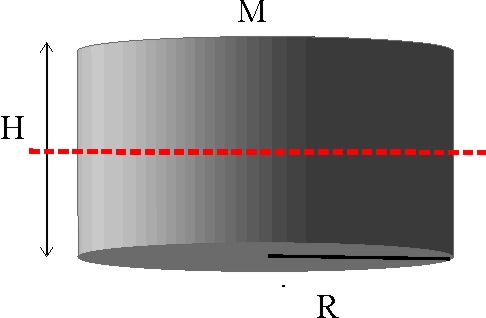
4.1.18. Si
dispones de un cilindro de radio R igual a su altura, podrás determinar que
la relación entre los momentos de inercia de éste, respecto a un eje tangente
a su perímetro, y de otro perpendicular al dado que pasa por el centro de
una de las bases es:
a) 1/2 b) 2 c) 3/2
d) 3
4.1.8. Una
chapa rectangular de base b y altura h cuya densidad superficial es
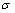 y masa m
puede girar alrededor de un eje que es paralelo a la base b y que pasa por
el centro de la chapa. El momento de inercia es:
y masa m
puede girar alrededor de un eje que es paralelo a la base b y que pasa por
el centro de la chapa. El momento de inercia es:
a)
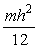 b)
b)
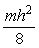 c)
c)
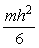 d)
d)
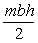
4.1.9. Una
chapa tiene forma de triángulo isósceles de base b y altura h. La chapa tiene
una densidad superficial es
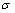 y un eje de giro paralelo a la base y que pasa
por el centro de masas, por tanto el momento de inercia es:
y un eje de giro paralelo a la base y que pasa
por el centro de masas, por tanto el momento de inercia es:
a)
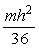 b)
b)
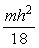 c)
c)
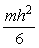 d)
d)
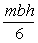
4.1.10. El momento de inercia
de una chapa de forma circular (radio R y masa m) respecto a un eje de giro
que coincide con uno de sus diámetros es:
a)
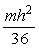 b)
b)
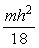 c)
c)
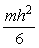 d)
d)
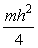
![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
![]()