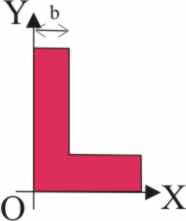3.1. DETERMINACIÓN DEL CENTRO DE MASAS
3.1.1.* El centro de masas de un cuerpo
o de un sistema de puntos materiales, es el punto de aplicación de la resultante
de todas las fuerzas exteriores que actúan sobre el sistema. Suele identificarse
generalmente con el centro de gravedad del cuerpo, pero esto sólo ocurre cuando:
a) EL CUERPO ES UN SÓLIDO HOMOGÉNEO
b) LAS FUERZAS EXTERIORES SON PRODUCIDAS POR EL
CAMPO GRAVITATORIO
c) EL CUERPO NO ES EXCESIVAMENTE EXTENSO
d) SIEMPRE COINCIDE CON EL CENTRO DE GRAVEDAD
e) LOS PUNTOS MATERIALES TIENEN TODOS LA MISMA MASA
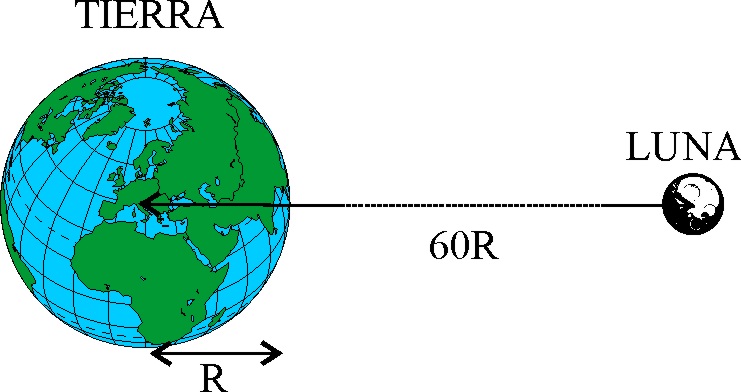
3.1.2. La masa de la Tierra es 81 veces
mayor que la de la Luna y la distancia entre sus centros es sesenta radios
terrestres (60 R). El centro de masas del sistema Tierra-Luna ocupa una posición
que está:
a) POR ENCIMA DE LA SUPERFICIE TERRESTRE
b) POR DEBAJO DE LA SUPERFICIE TERRESTRE
c) A LA MITAD DE LA DISTANCIA ENTRE AMBOS CUER-POS
CELESTES
d) INDETERMINADA, YA QUE DEPENDE DE LAS FASES DE
LA LUNA
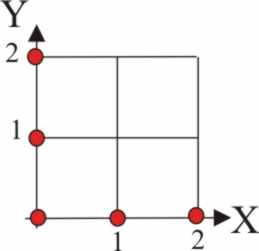
3.1.3. El centro de masas de un sistema
formado por cinco masas puntuales iguales colocadas en la forma que indica
la figura, está en la bisectriz del ángulo y a una distancia del vértice de:
a)
![]() b)
b)
![]()
c)
d)
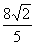
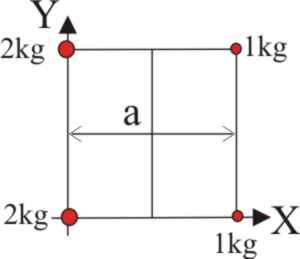
3.1.4. En los vértices de un cuadrado de
lado a se sitúan cuatro masas tal como indica la figura. Si en el medio de
la recta que une las masas de 1 kg se sitúa una masa de M kilos, resulta que
el centro de masas del sistema formado está en el centro de dicho cuadrado,
por tanto el valor de M es:
a)
1 b) 2
c) 3 d)
4 e) 5
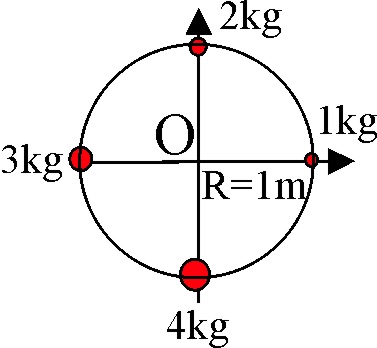
3.1.5. Cuatro masas puntuales de 1, 2, 3
y 4 kg respectivamente están situadas sobre una circunferencia de radio unidad
tal como indica la figura.
Se
añade una quinta masa M, en un lugar de la circunferencia de modo que el centro
de masas de todo el sistema se encuentre en el punto O. El valor de la masa
añadida M, expresada en kilogramos, es:
a)
2/2 b) 3/2 c) 6
d) 8/2/3
y
las coordenadas del lugar que ocupa M son:
a)
![]() ) b)
) b)
![]()
c)
d)
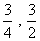
3.1.6. El lugar geométrico del centro de
masas de todos los sistemas formados por dos puntos materiales de masas m
y 2m situados respectivamente sobre los ejes X e Y y a igual distancia del
origen, deberá ser:
a)
LA RECTA BISECTRIZ
b)
LA RECTA DE ECUACIÓN y=2x
c)
UNA RECTA DE ECUACIÓN y=2x/3
d)
UNA RECTA DE ECUACIÓN y=3x/2
e)
NADA DE LO DICHO
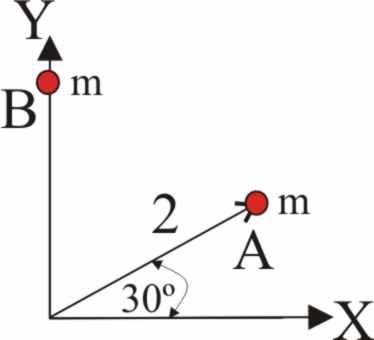
3.1.7. Dos puntos materiales A y B de masas
iguales están situados en el plano XY. A viene determinado por un vector de
posición cuyo módulo vale 2 y forma un ángulo de 30 grados con el eje X, mientras
que B se puede encontrar en cualquier punto del eje Y. Por ello dirás que el lugar geométrico de
las posiciones del centro de masas del sistema deberá ser:
a)
UNA RECTA QUE PASA POR EL PUNTO 0,0 CON PENDIENTE 2/3
b)
UNA RECTA PARALELA AL EJE Y
c)
UNA CIRCUNFERENCIA
d)
UNA PARÁBOLA
e)
NADA DE LO DICHO
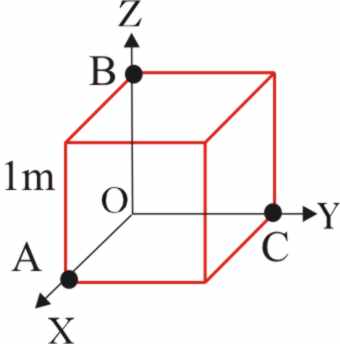
3.1.8. En los vértices A, B y C del cubo
de lado 1m de la figura, se encuentran tres masas iguales, m. Por lo tanto
el centro de masas de la figura deberá estar en:
a)
EL CENTRO DE LA DIAGONAL DE LA CARA SUPERIOR
b)
EL CENTRO DE CUALQUIER DIAGONAL DEL CUBO
c)
EL CENTRO DE LA DIAGONAL DE LA BASE DEL CUBO
d)
UNA PERPENDICULAR AL CENTRO DE LA BASE DEL CUBO
e)
EL PUNTO (1/3, 1/3, 1/3)
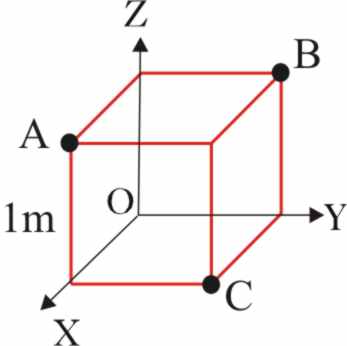
3.1.9. En los vértices A, B y C del cubo
de lado 1m de la figura, se encuentran tres masas, m, 2m y 3m, respectivamente.
Por lo tanto el centro de masas de la figura deberá tener como vector de posición
r:
a)
![]()
b)
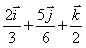
c)
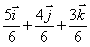
d) UN VECTOR CUYAS COMPONENTES X,Y,Z SEAN UNA PROGRESIÓN
ARITMÉTICA CUYO PRIMER TÉRMINO SEA 3/6, Y RAZÓN 1/6
e) NADA DE LO DICHO
3.1.10. Si tomas un alambre de 70 cm y lo
doblas en ángulo recto de forma que uno de los lados sea de 30cm, dirás que
el centro de masas de la figura formada se encuentra en:
a) LA BISECTRIZ DEL ÁNGULO RECTO
b) EL VÉRTICE DEL ÁNGULO RECTO
c) EL PUNTO MEDIO DE LA RECTA QUE UNE LOS DOS EXTREMOS
d)
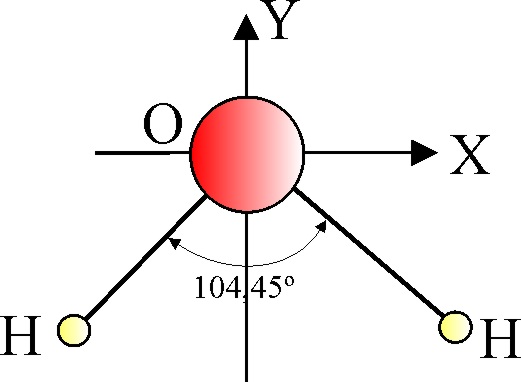
3.1.11. En la figura se encuentra una versión
simplificada de la molécula de agua. La longitud del enlace O-H es 0,09584
nm y el ángulo de enlace H-O-H 104,45E. El centro de masas de esta molécula respecto
a los ejes dibujados están en el eje Y siendo el valor de dicha coordenada
expresada en nm:
a)
-6,53·10-3 b) -4,35·10-3 c) -3,87·10-3
d) -2,47·10-3
3.1.12. Una barra cilíndrica de longitud
L tiene una densidad que no es constante a lo largo de ella, sino que crece
linealmente desde un valor
![]() en un extremo A hasta 2r en el extremo B. El centro de masas de dicha barra está
a una distancia de A igual a:
en un extremo A hasta 2r en el extremo B. El centro de masas de dicha barra está
a una distancia de A igual a:
a) L/2 b) 3L/7
c) 3L/8 d) 5L/8
e) 5L/9
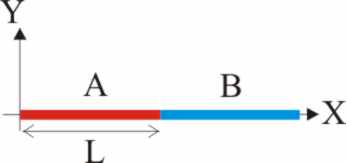
3.1.13. Se sueldan, una a continuación de
otra, dos varillas homogéneas A y B de la misma longitud L pero hechas de
dos materiales diferentes, siendo la densidad de A doble que la de B. El centro
de masas del conjunto se encuentra a una distancia del extremo de A igual
a:
a) L/2
b) 3L/7 c) 3L/8
d) 5L/6 e) 5L/9
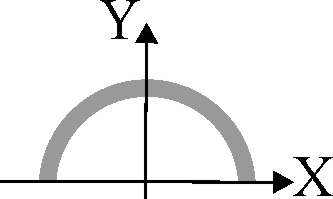
3.1.14. Con un alambre fino de sección constante
se moldea una semicircunferencia de radio R. El centro de masas se encuentra
en el eje de simetría a una distancia del centro de la circunferencia a la
que pertenece la figura igual a:
a) R/p b)
2R/p c) R/2p d) R/2
3.1.15. Calcular el centro de masas de una
varilla de longitud L, no homogénea, cuya densidad lineal varía con la longitud
según la relación (4-x/5) kg/m, siendo x la distancia desde el extremo más
denso a cualquier punto de la varilla. La densidad lineal mínima de esta varilla
es de 2 kg/m. El c.d.m. de la varilla
se encuentra a una distancia del extremo de mayor densidad lineal. igual a:
a)
2,2m b) 4,4m c) 6,6m
d)
8,8m e) NINGUNO DE LOS VALORES
DADOS
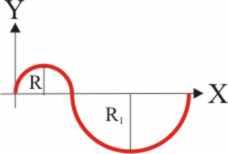
3.1.16. Con un alambre de sección uniforme
se moldea una figura formada por dos semicircunferencias de radios R y R1
siendo R1=2R, respecto de los ejes dibujados en la figura dada,
la coordenada X del centro de masas es:
a) R/2 b) R
c) 2R d) 3R e) 4R
y la coordenada Y es:
a)
-R/
![]() b) -R/2
b) -R/2
![]()
c) -2R/
d) -3R/2
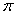
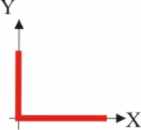
3.1.17. * Como eres muy aficionado a la
física, has convertido tu habitación en una especie de laboratorio de mecánica,
con construcciones y disposiciones de objetos en raros equilibrios. Para rematarlo
decides hacer una L mayúscula recortándola de una cartulina, de forma que
su parte vertical sea 4 veces el ancho b, mientras que la base horizontal
sólo lo sea 3, y después clavarla por su centro de masas, con una chincheta
en el marco de madera. Sin embargo esta operación te va a resultar extremadamente
difícil porque:
a) EL EQUILIBRIO ES INDIFERENTE SI SE CLAVA EN CUALQUIER
PUNTO DE LA PARTE VERTICAL
b) QUEDARÍA EN EQUILIBRIO EN EL CENTRO DE LA BASE
HORIZONTAL
c) EL CENTRO DE MASAS DE
d) EN UN SISTEMA DE REFERENCIA CENTRADO EN EL VÉRTICE
INFERIOR IZQUIERDA DE LA L, EL CENTRO DE MASAS TENDRÍA UNA POSICIÓN DADA POR
EL VECTOR:
![]()
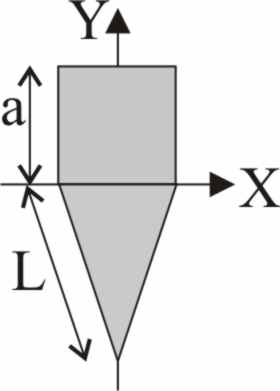
3.1.18. De una plancha de cartón piedra
recortas un cuadrado de lado a y un triángulo isósceles de lados iguales L,
y cuya base se adapta al cuadrado. La relación
que deberá existir entre L y a para que el centro de masas del sistema esté
situado en el punto medio de la unión de ambas figuras, tal como indica el
esquema deberá ser :
a)
1 b) 1,5
c)1,8
d)2 e)NINGUNO DE LOS VALORES DADOS
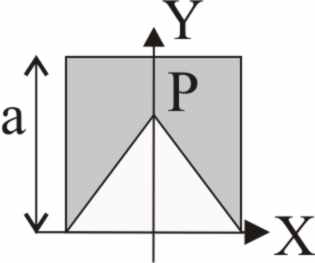
3.1.19. Si a la plancha cuadrada anterior,
le recortas un triángulo isósceles cuya base es un lado a y el vértice un
punto P tal que sea el centro de masas de la nueva figura, la superficie de
ésta será:
a) EL DOBLE DE LA PARTE EXTRAÍDA
b) MENOS DEL DOBLE DE LA PARTE EXTRAÍDA
c) MÁS DEL DOBLE DE LA PARTE EXTRAÍDA
d) IGUAL A LA DE LA PARTE EXTRAÍDA
e) NINGUNO DE LOS VALORES DADOS