ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA

4.3. TRABAJO Y ENERGÍA DEL SÓLIDO EN ROTACIÓN. CONSERVACIÓN. (1ª parte)

 

 

4.3.1. Tomas un cuadrado rígido de masa M y lado L, lo sujetas por dos vértices opuestos, y lo haces girar con una velocidad angular w. Su energía cinética de rotación será:

a) ML²w²/12              b) ML²w²/24             c) ML²w²/4                 d) ML²w²/2             

 

 

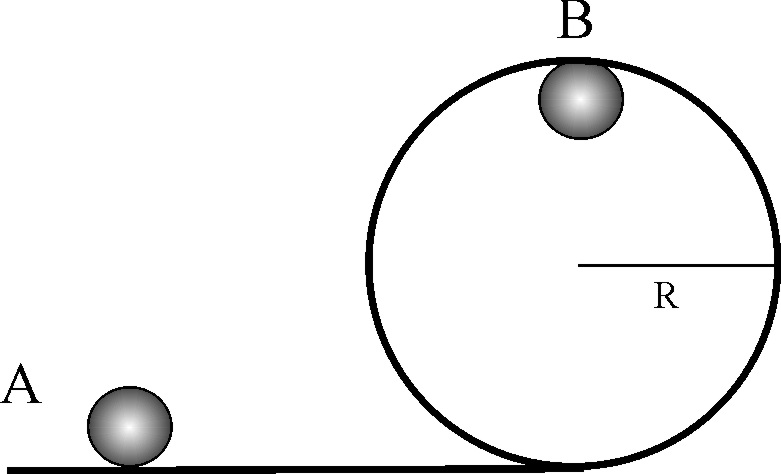
4.3.2. Cuando una esfera rueda por un plano con velocidad de traslación v_CM y de rotación ω la energía cinética de rotación es respecto a la total:

a) 1/5          b) 2/5               c) 2/7                   d) 1/2    

 

 

4.3.3. Un cuerpo se traslada y gira al mismo tiempo sin deslizar (rueda). Se observa  que su energía cinética de rotación es igual que la de su traslación del centro de masas, concluirás que:

a)  SE TRATA DE UN CILINDRO MACIZO

b)  SE TRATA DE UNA ESFERA MACIZA

c)  SE TRATA DE UN ARO

d)  NO EXISTE UN CUERPO QUE CUMPLA LAS CONDICIONES DEL ENUNCIADO

 

 

4.3.4. Si la masa de un vehículo de fórmula 1 es 50 veces la de una rueda (considerada como un cilindro hueco), la relación entre las energías cinéticas de traslación del mismo y de rotación de sus ruedas, será:

a) 0,87             b) 1,14            c) 1,00            d)  12,5

 

 

4.3.5. Las moléculas de los gases no sólo pueden desplazarse, sino que también giran, y por lo tanto tienen una determinada energía cinética de rotación, con la cual contribuyen a su capacidad calorífica. Si conoces la distancia de enlace Cl-H (r=0,1275 nm), y que la masa del Cl es aproximadamente 35,5 veces la del hidrógeno , (1u = 1,66.10^-27kg), podrás afirmar que la energía cinética de rotación de la molécula de cloruro de hidrógeno cuando  gira alrededor de un eje perpendicular al de enlace que pasa por su centro de masas con una frecuencia N, es en julios:

a) 5.10^-6N²          b) 2,5.10^-16N²        c) 5.18.10^-26N²             d)  5,18.10^-46N²                     

 

4.3.6. Si la bola de la figura masa m y radio r, se lanza desde A  rodando, la velocidad mínima que debe dársele para que sobrepase sin caer la parte más alta del rizo de radio R, despreciando cualquier rozamiento deberá ser:

a)                 

b)                   

c)                

d)      

 

 

 

4.3.7. En el dispositivo de la figura la relación entre las mínimas alturas, H₁ y H₂, a las que se debe situar la esfera de radio r, para que sobrepase el rizo de radio R sin caerse, cuando baja rodando (H₁) o si lo hiciera deslizando sin rozamiento (H₂) será:  

a) 1,05             b) 1,08            c) 1,09            d) 1,06       

 

 

 

                                          

 

 

4.3.8.* Si una esfera de masa m, se deja caer rodando por una pista desde el punto A, a una altura H=3R, siendo R el radio de un rizo incluido en dicha pista, podrás decir de las fuerzas centrípetas  que actúan  sobre la esfera, en su punto más alto D, el más bajo B, y el intermedio C que:

a)  LA DEL PUNTO MÁS ALTO ES EL TRIPLE DE LA DEL MÁS BAJO

b)  LA MENOR TIENE LUGAR EN EL PUNTO C

c)  EN EL PUNTO MÁS BAJO ES IGUAL AL PESO

d)  EN EL PUNTO C ES IGUAL A LA QUE TIENE EN EL PUNTO OPUESTO

 

 

4.3.9. Si dejas rodar una pequeña esfera metálica por una pista, con un rizo de radio R, desde una altura h, observas que se despega de la pista, cayendo  al suelo. Ahora bien si pretendes que al caer pase justamente por el centro del rizo, esa altura h, prescindiendo de todo rozamiento, será de:

a) 1,50R                b) 1,85R              c) 1,98R        d) 2,25R       

 

 

 

4.3.10. Si abandonas una esfera de radio r en el punto más alto de una cúpula semiesférica de radio R=10r, de forma que descienda rodando, el desplazamiento angular que habrá realizado la esfera pequeña, hasta que se despega de la cúpula será aproximadamente en radianes:

a) 3π                     b) 2p               c) p            d) p/2