ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA

3.3. CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO (masa variable)

  

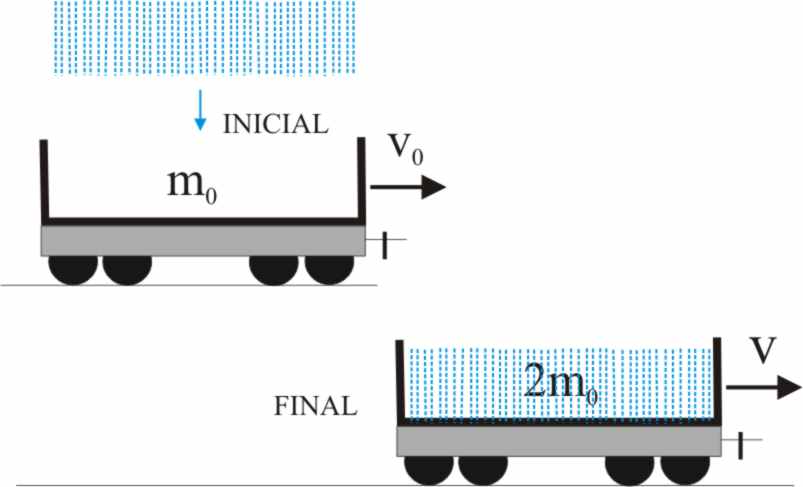
3.3.31.* Un contenedor impermeable, abierto por la parte superior con una capacidad tal que su masa lleno de agua es el doble que cuando está vacío, m₀ y se dispone sobre una plataforma móvil que rueda sin rozamiento por una vía rectilínea a una velocidad  m/s. Comienza a llover de forma que el ritmo con que se llena el contenedor es  de  n kg/s. En esta situación podrás afirmar que:

     a) EL CONTENEDOR MANTIENE SIEMPRE LA MISMA VELOCIDAD

     b) EL CONTENEDOR ADQUIERE UN MOVIMIENTO UNIFORMEMENTE RETARDADO         

     c)  EL CONTENEDOR TERMINARÁ DETENIÉNDOSE

     d) LA MÍNIMA VELOCIDAD ALCANZADA POR  EL  CONTENEDOR  ES

     e) EL RECORRIDO EFECTUADO POR EL CONTENEDOR HASTA LLENARSE ES DE

 

 

 

3.3.32. Si el contenedor anterior fuera arrastrado por una locomotora, por los raíles con los que el coeficiente de rozamiento es , para que mantuviera durante el tiempo de llenado por la lluvia una velocidad constante , la locomotora tendría que aplicar una fuerza horizontal sobre el contenedor  y la potencia desarrollada por esa fuerza cuando la de rozamiento es máxima, vale, expresada en vatios:

 a) v₀( v₀ + 2 m₀g)                   

b) v₀(nv₀ - 2 m₀g)       

 c) v₀( m₀g - nv₀)                                               

d) v₀²(n m₀g)

                                                                           

 

 

3.3.33. Los camiones de riego que en las madrugadas suelen limpiar nuestras calles, son un claro ejemplo de un sistema que debe procurar mantener una velocidad constante pese a la pérdida continua de masa. Si un camión cisterna, tiene una masa m, cuando está completamente cargado, y va lanzando un chorro de agua con velocidad  respecto del camión, en sentido contrario al de su marcha, siendo el régimen de gasto de agua n kg/s. La potencia disipada en vatios para lograr  que el camión mantenga su velocidad constante es:

                   a) unv                             b) u²n/v                                             c) - nv²/u 

                   d) - uvn                          e) NADA DE LO DICHO

 

 

3.3.34. Los núcleos atómicos inestables (fuera de la franja de estabilidad), se desintegran espontáneamente emitiendo partículas que salen a gran velocidad, lo cual deberá provocar una gran variación de la cantidad de movimiento del núcleo inicial. Si uno de masa m, lanza una partícula de masa cinco veces menor, con una velocidad , el residual se desplazará con velocidad:

 a) 5           b) -5        

c)         d)

 

 

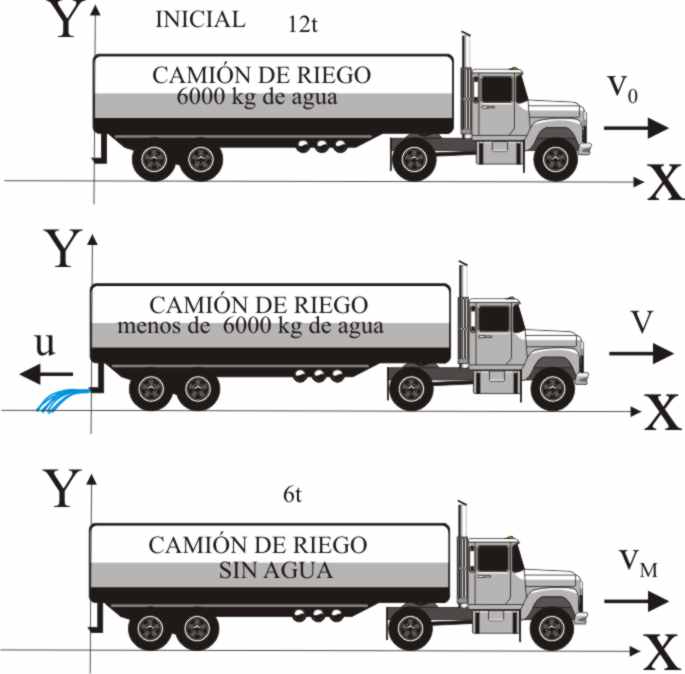
3.3.35.* Imaginemos que un camión aljibe, con un peso bruto de 12 t, y una tara de 6000 kg, sólo se moviera, por efecto de la salida del agua de riego, con un ritmo continuo de 20 litros por minuto, y una velocidad  de 1m/s respecto del camión. Si inicialmente antes de comenzar a regar su velocidad era de 10 km/h, dirás que:

     a) SÓLO PODRÁ REGAR DURANTE 5 HORAS

     b) SU VELOCIDAD MÁXIMA FUE DE  12,5 km/h.

     c) SU ACELERACIÓN MEDIA FUE DE  0,2 m/s².

     d) AL CABO DE 2 HORAS SU VELOCIDAD SERÍA DE  10,8 km/h.

 

 

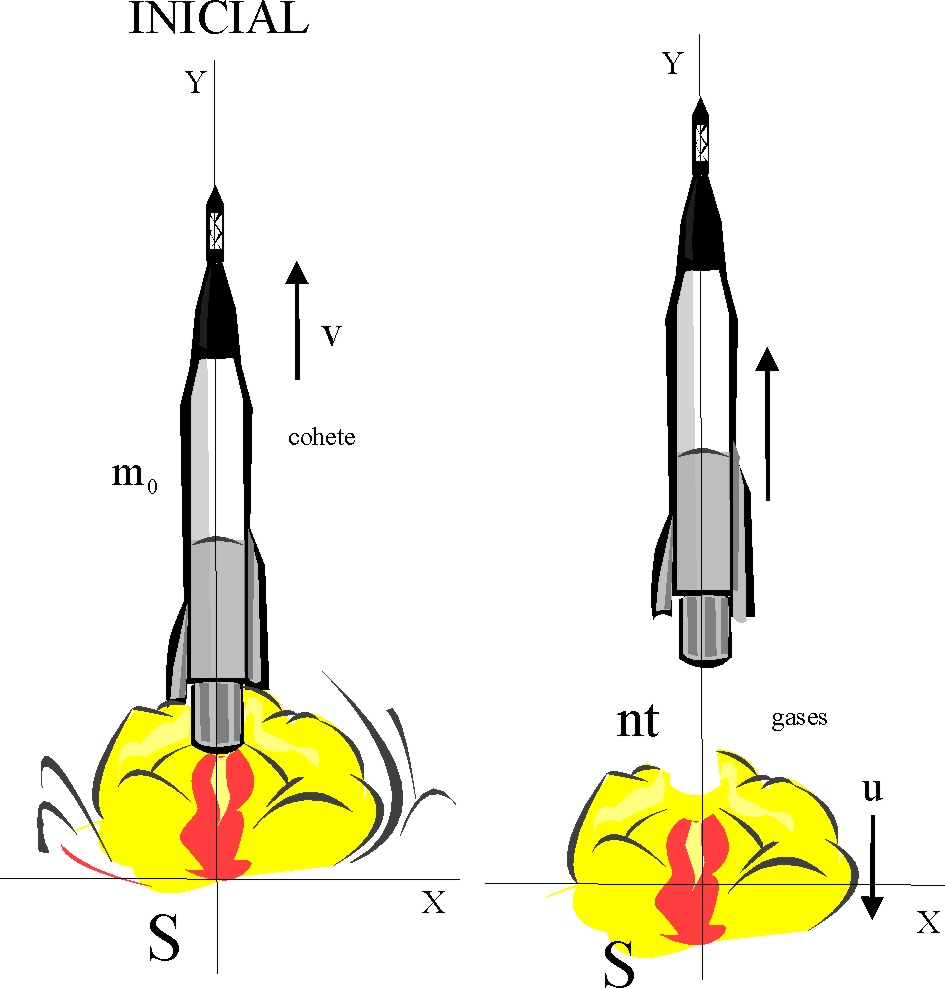
3.3.36.* El movimiento de los cohetes interplanetarios se basa en el efecto de la propulsión a chorro, aplicado a los motores de avión a partir de 1941, esto es los gases producidos en la combustión de del propelente, las tres cuartas partes de la masa total m₀, salen con una velocidad u respecto a la del cohete, con lo cual éste va incrementando su velocidad. Si la  masa antes de la expulsión de gases a un ritmo de n kg/s, es m₀, podrás decir que en el campo gravitatorio terrestre (suponiendo las variaciones de g =9,8 m/s², despreciables) así como la resistencia del aire

   a)  EL MOVIMIENTO QUE REALIZA EL COHETE INICIALMENTE ES UNIFORMEMENTE    RETARDADO

   b) SÓLO EL MOVIMIENTO SERÁ UNIFORMEMENTE RETARDADO AL CABO DE  UN TIEMPO t= 3m₀/4n

       c)  EL COHETE TIENE SU VELOCIDAD MÁXIMA AL SALIR

       d)  LA MÁXIMA VELOCIDAD ES 1,39  .

 

 

3.3.37. Los cohetes interplanetarios, van quemando combustible, frecuentemente oxígeno e hidrógeno líquido, que produce unos gases que salen con una velocidad constante , respecto a la del cohete y por lo tanto su masa disminuirá. En ausencia de interacciones gravitatorias, cuando su masa sea la cuarta parte de la inicial, la velocidad del cohete será en valor modular respecto a la de los gases expulsados un número de veces igual a :

                   a) 1                                b) 1,38                           c) 0,69           

                   d) 0,1                             e) NADA DE LO DICHO

 

 

3.3.38. Cuando la velocidad de un cohete interplanetario fuera de un campo gravitatorio respecto a un observador inercial es igual a la de salida de sus gases, su masa se habrá reducido a:

     a) LA MITAD                                                     b) LA CUARTA PARTE

     c) TRES CUARTAS PARTES                            d) POCO MAS DE UN TERCIO

     e) NADA DE LO DICHO

 

3.3.39. Hace algún tiempo hemos observado por la televisión el lanzamiento del primer satélite espacial español, el Hispasat. Al principio parecía que iba muy lento, y después aumentaba su velocidad hasta desaparecer. Si consideramos que el cohete con satélite y combustible tiene una masa inicial de 100t, que las tres cuartas partes de aquella, corresponden al combustible y que su combustión produce unos gases que salen expulsados con una velocidad de 4.000 m/s, respecto al cohete, siendo el gasto de combustible 10000 kg/s, podrás asegurar, por lo tanto, si g=9,8 m/s², y despreciamos la resistencia del aire que:

     a) LA MÁXIMA VELOCIDAD ALCANZADA SERÍA 5472 m/s.

     b) AL CABO DE 1s, SU VELOCIDAD ERA TAN SOLO DE 412 m/s.

     c) EL TIEMPO DE COMBUSTIÓN DE LOS GASES FUE DE 7,5s.

     d) LA  MITAD DE LA VELOCIDAD MÁXIMA SE VERIFICA EN EL TIEMPO 3,75 SEGUNDOS

     e)LA ACELERACIÓN DEL HISPASAT, MIENTRAS QUEMA COMBUSTIBLE, ES DIRECTAMENTE PROPORCIONAL AL TIEMPO.