GRUPO HEUREMA. EDUCACIÓN SECUNDARIA

ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
sección: TEMAS DE FÍSICA Y QUÍMICA
para imprimir(pdf)
volver a inicio
                                 

 

 

 

 

ORBITALES ATÓMICOS HIDROGENOIDES d (primera parte)

Si los orbitales atómicos p tenían bastante complejidad ¿qué decir de los d? El alumno de enseñanzas medias, dibuja un trébol de cuatro hojas, que toma como modelo de este orbital y se queda tan tranquilo, sin enterarse de lo que está haciendo.

La condición cuántica que lo determina es l=2 y las funciones radiales que se deben representar corresponden a  valores de R que para n=3, y para n=4, tienen las siguientes ecuaciones:

     y    

 

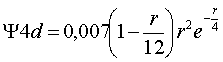
Si se representan en una hoja de cálculo se obtienen las  gráficas, correspondientes a las figuras 1 y 2

 

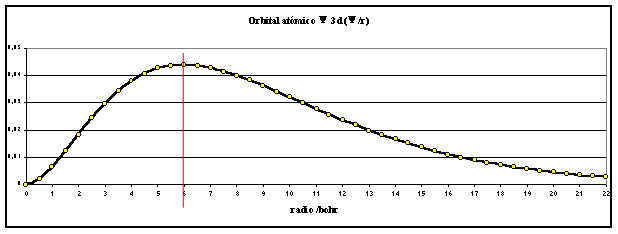
fig. 1

  
                       
   

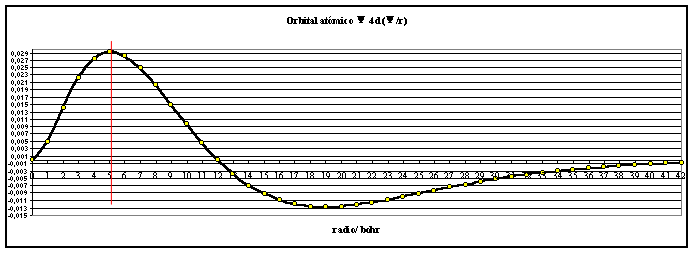
fig.2
                       

En la función R 4d, se observa que para r=0 y para r=12, la función se anula. Este último valor va a generar una superficie nodal ( superficie interior cuya densidad de probabilidad es nula)

Si las funciones dadas se elevan al cuadrado y se multiplican por r2, se obtiene la densidad de probabilidad radial (fig. 3 y 4).
                       
     

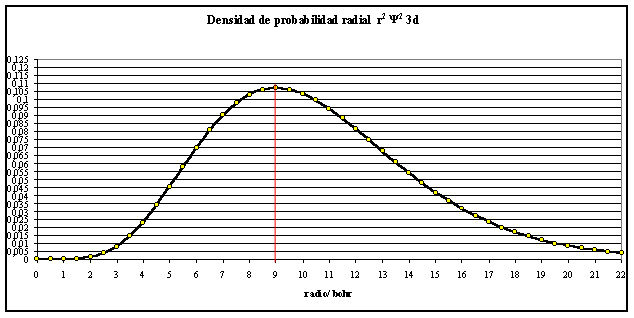
fig.3
                                   
 

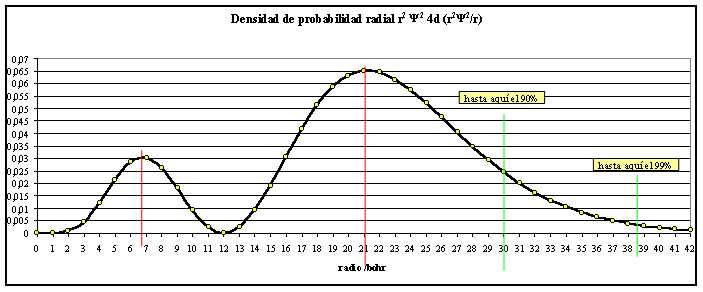
fig.4

    
                                   
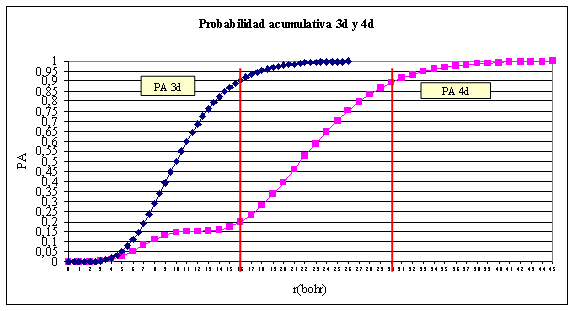
Las propiedades acumulativas revelan que hasta el 90%, las distancias máximas se separación son de 16 y 30 bohr respectivamente (fig. 5)
       

fig.5

      
                                   

La contribución angular a la función de onda total, es en este caso muy grande, y depende de los valores que tome el número cuántico m. Para  m=0, se obtiene la función R dz2. Para valores de m=1,-1 sería R dxz  y  R dyz y si m = 2, y -2 ; R xy y R d (x2-y2).

 

Otra de las preguntas características de los alumnos de enseñanzas medias respecto a los nombres de los orbitales d, es ¿De dónde sale el orbital 3dxy?. ¿En qué se parece y diferencia del 3dxz? ¿Y del 4dxy?

Para explicarlo no queda mas remedio que ir a las ecuaciones de definición  consierando la contribución radial y angular y que al ser representadas darán los diferentes OA d.

Serían:

 

      ;      ;        

 

 
                                   
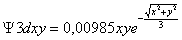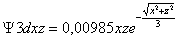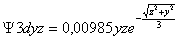
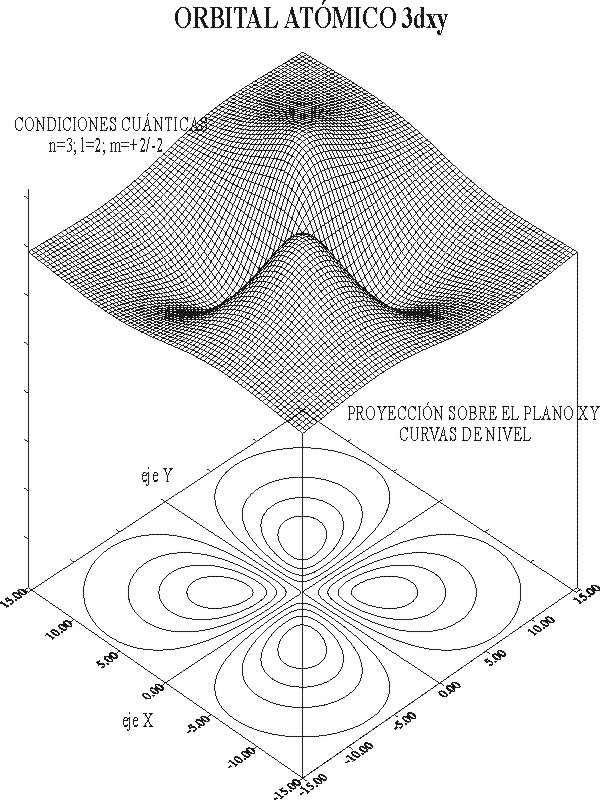
Como se aprecia, las tres funciones son similares, lo único diferenciante es el plano en que se representan en función de las variables que intervienen. Así obtendríamos los tres orbitales d, de la misma forma, el 3dxy, 3d xz y 3dyz, con planos nodales coincidentes con dichos ejes. Obsérvese en las figuras 6 y 7, la forma de la función superficie para el orbital 3dxy y el detalle de las curvas de nivel, siempre en unidades bohr de distancia atómica, en los ejes correspondientes.
         

fig.6

        
                                   
         

 

 

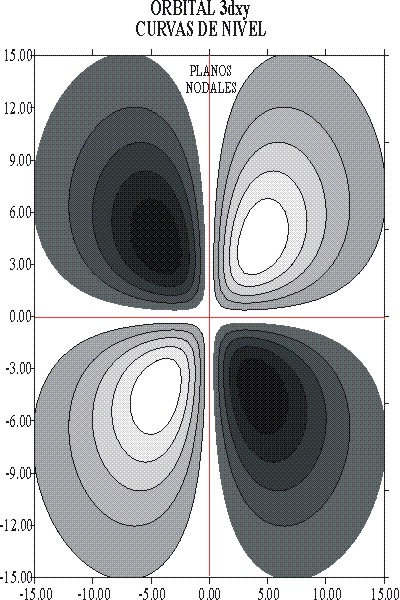
fig.7

        
                                   
 

Las zonas mas oscuras corresponden a valores de R3d negativos (valles), mientras que las mas claras corresponden a valores positivos (montañas), en la gráfica  de superficie.

La función R elevada al cuadrado y representada daría lugar a la descripción de la densidad de probabilidad correspondiente. En la fig. 8 la línea de contorno que abarca el 90% de probabilidad, se considería lo que habitualmente se dibuja como el OA 3dxy. En la fig 9, se aprecia el detalle de las curvas de nivel de probabilidad.
                                   

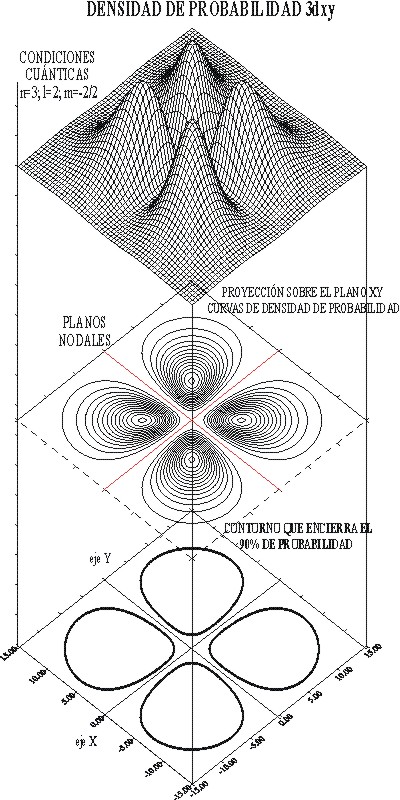
fig.8

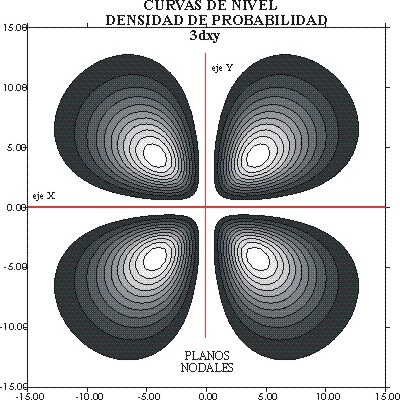
fig.9
 

Se va a comparar ahora este orbital con el  4dxy, sobre todo para romper los tópìcos sobre su igualdad respecto a 3dxy. Es evidente que el tamaño no puede ser el mismo, como se aprecia en la función de distribución radial, pero tampoco lo es la forma, en contra de lo que parece.

 

La ecuación de la función R4dxy, es completamente distinta:

 

 

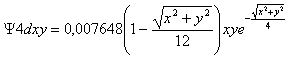
Lo cual indica un punto nodal, cuando el factor binómico se anule. Este punto nodal engendrará una superficie nodal, o sea una superficie interior en la que la probabilidad de encontrar al electrón es nula, que será el factor diferenciante en la forma del orbital frente al 3dxy.

 

La representación de la función de onda, y el detalle de las curvas de nivel, se dan en las figuras 10 y 11. A través de ellas se puede diferenciar perfectamente ambos orbitales atómicos.

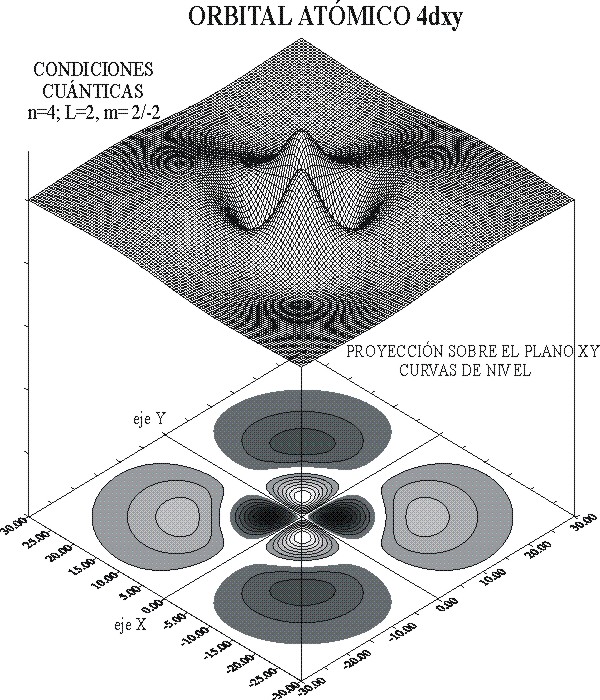
fig.10
   

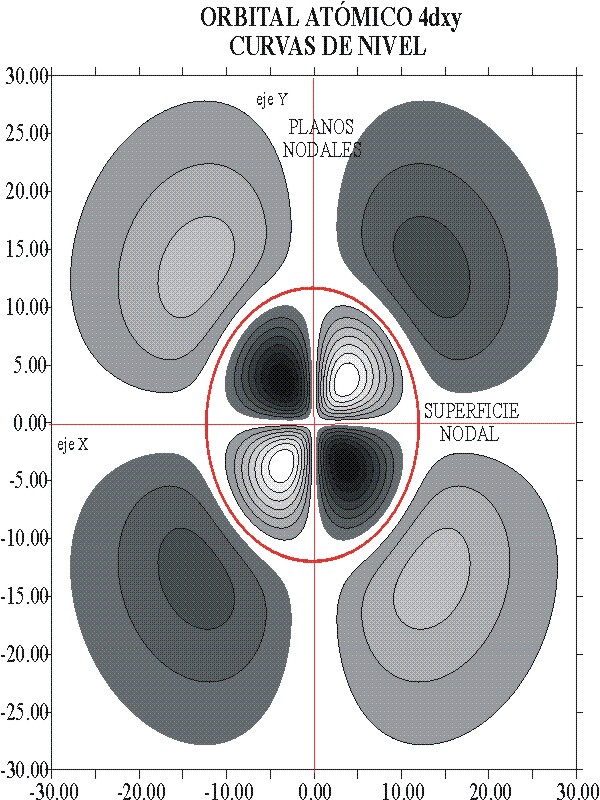
fig.11

También los dibujos permiten diferenciar, los planos nodales de las superficies nodales. Los primeros como dependen única y exclusivamente del valor de l, que es 2 para los orbitales d,  ya sean 3d o 4d, es un elemento de analogía, mientras que las superficies nodales que dependen de n-(l+1), es diferenciante.

Para el 3d,  las superficies nodales serían 3-(2+1)= 0, mientras que para el 4d; 4-(2+1)=1.

En las gráficas dadas, siguiendo el criterio general presentado en estos trabajos, a los valles, valores negativos, les corresponden las zonas mas oscuras mientras que a las cumbres, valores positivos, les corresponden las zonas mas claras.

Tampoco la forma de las curvas de nivel es la misma. El acotamiento al 90%, en zonas de muy poca pendiente, hace que aparezcan eliminadas zonas superficiales que modifican el trazado habitual.

Las gráficas de las densidades de probabilidad para estas funciones, se exponen las figuras 12, y 13.
 

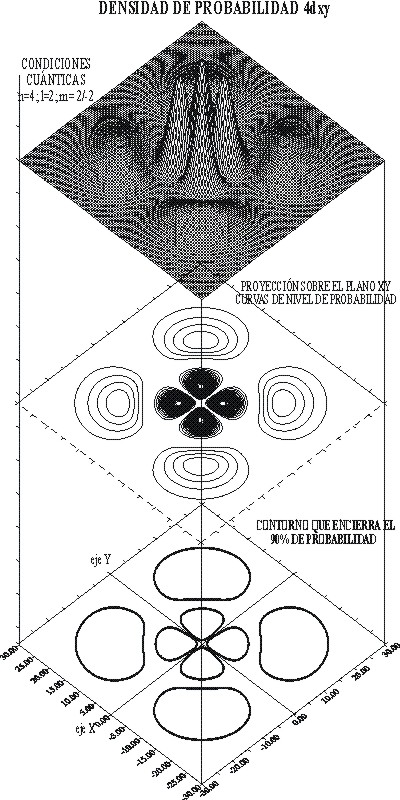
fig.12

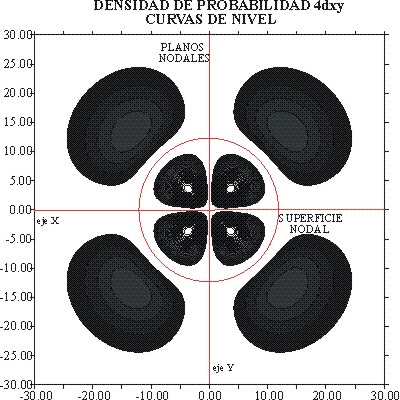
fig.13
     

En estas gráficas, los valores de la función al estar  elevados al cuadrado siempre van a ser positivos, y por lo tanto no existe el criterio de tonalidades de grises anterior.

En la distribución espacial de lo que se considera como orbital atómico, haciendo girar la figura plana por el eje X,  las superficies nodales interiores, quedan tapadas, y no se apreciarían.