ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
ORBITALES ATÓMICOS HIDROGENOIDES p
La
enseñanza del tema de orbitales
atómicos en
Muchas veces hemos escuchado comentarios tan curiosos referidos a los orbitales p como que “los electrones hacen ochos junto al núcleo”, que ¿cómo era posible que un electrón pasara por el núcleo desde una parte del orbital a otra? Para intentar que comprendan esto, diremos que los orbitales atómicos son consecuencia de un tratamiento matemático, partiendo de la ecuación de una onda, al cuadrado de su característica fundamental o función de onda se le atribuyó un significado físico asociándolo a la densidad de probabilidad de encontrar al electrón, a una determinada distancia del núcleo atómico. Así como se ha visto en el tema de OAs, la máxima densidad de probabilidad radial para la función R1s, coincidía con el radio de Bohr para el hidrógeno en su estado fundamental.
Funciones de onda R p radiales
Para
representar los OAp se han elegido las funciones de onda y del hidrógeno para los
diferentes valores de los números cuánticos n, siempre con l=1. (figuran
en cualquier libro de Química Inorgánica o de Química
Física de nivel universitario).
Las
ecuaciones que dan los valores
de R para n=2, l=1 y n=3, l=1,
en su expresión radial, aplicadas al átomo de hidrógeno (Z=1) y en función
del radio de Bohr, son respectivamente:
![]() y
y
![]()
Los
factores numéricos k que aparecen multiplicando ambas funciones se determinan
con las condiciones de normalización, que implican que la probabilidad
total de encontrar al electrón en el espacio es 1.
Así,
aplicando
![]() , se obtiene que k1=0,204 y k2=0,0202.
, se obtiene que k1=0,204 y k2=0,0202.
Si
se representan mediante una hoja
de cálculo, se obtienen las siguientes gráficas:
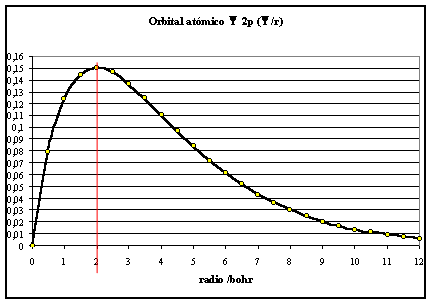
Fig.1
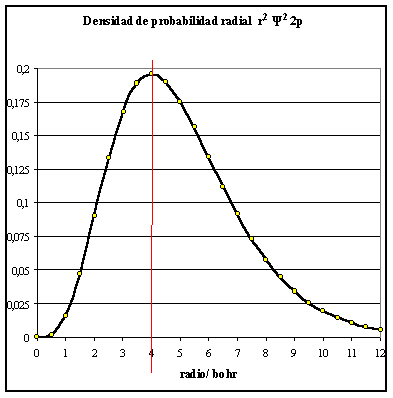
fig.2
Si la función R se eleva al cuadrado , se obtiene la densi-dad de probabilidad, que multiplicada por r2, da la densidad radial de probabilidad.
La
gráfica de la figura 2 representa esa densidad
radial de probabilidad frente a r, en bohr. En la misma se aprecia un máximo a 4 bohr
del núcleo.
Orbitales atómicos 3p
Repitiendo el proceso para la función 3p se obtienen las figuras 3 y 4
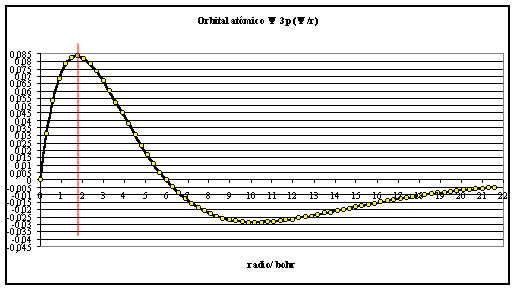
fig.3
En la figura 3 el máximo de R3p en función del radio está a 1,8 bohr (hay un efecto de penetración o acercamiento al núcleo al aumentar n), pero en la figura 4, se observa que el primer máximo de la densidad radial de probabilidad tiene lugar a unos 3 bohr de distancia al núcleo, mientras que el segundo lo hace a unos 12 bohr.
La función se anula para valores de r = 0 y 6 bohr. Este último valor indica que a esa distancia existe una superficie nodal, esto es, una superficie en la cual la densidad radial de probabilidad es cero.
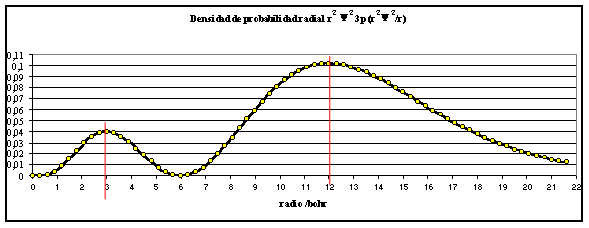
fig.4
La
representación de la función que da la probabilidad acumulativa (PA) con
la distancia al núcleo para los OAp realizada mediante cálculo numérico
a partir de la suma de los valores r2R2 multiplicada por dr,
se muestra en la fig 5.
Si
se considera el OA como la superficie que encierra el 90% de densidad
radial de probabilidad, se tendrá que para el OA 2p, la distancia de extensión
es de 8,1 bohr (si fuera el 99% sería 11 bohr), mientras que para el OA
3p, es de 18,5 bohr (para el 99% sería de 24,5 bohr).
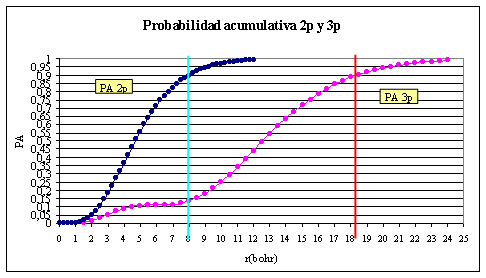
fig.5
Todo
lo anterior hace referencia a las funciones radiales.
OA p sobre los ejes de
coordenadas cartesianas.
Sin
embargo para orbitales determinados por condiciones cuánticas en las que
l>0, la componente radial se ve influenciada por una componente angular
que condicionará la forma del orbital y modificará las zonas de máxima
probabilidad. Ahora existirán tres variables:
r, y los ángulos N y 2, que forma r con los ejes
.
De
esta forma la función R debe reunir ambas componentes,
tomando similares valores para cada par (n,l). Según el valor empleado de m (1, 0, y -1) se orientará sobre diferente eje de coordenadas.
Para
representar el OA de forma completa, se usará un programa de dibujo tridimensional,
en ejes cartesianos, lo que implicará pasar de coordenadas polares a rectangulares
con las conversiones necesarias.
En
este caso x= r sen Ncos 2, y = r sen N sen 2, y z= r cos 2 y r2 =
x2+y2+z2
Las
funciones características de los orbitales atómicos 2p toman las expresiones
siguientes para el caso del hidrógeno Z=1,y en función del radio de Bohr:
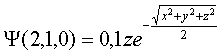 que corresponde
al OA 2pz
que corresponde
al OA 2pz
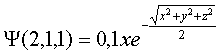 que
corresponde al OA 2px
que
corresponde al OA 2px
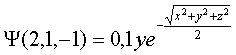 que
corresponde al OA 2py
que
corresponde al OA 2py
Se
va a representar como ejemplo la función R2px. El programa
matemático empleado, genera una malla superficial, en la que cada
punto (x,y) corresponde valor de y. Como se trabaja sobre el plano XY, se
hace z=0.
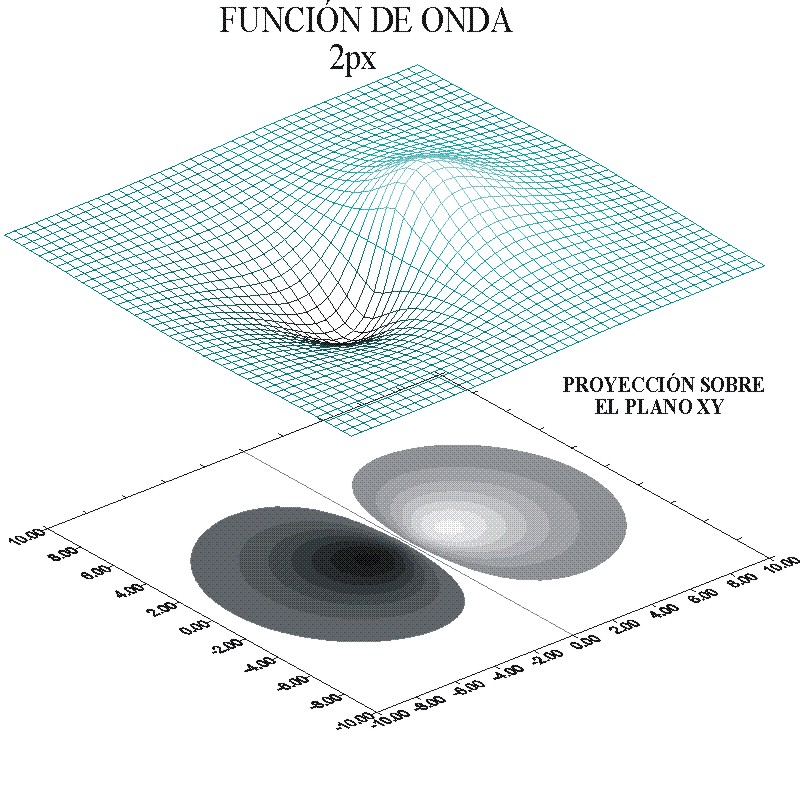
fig. 6
Dado que los valores de y pueden ser positivos o negativos, la malla superficial contendrá “montañas y >0 y “abismos”, y <0. Los abismos corresponden a valores negativos y en los dibujos se representan en la escala de grises hacia el negro; cuanto más oscuro, más negativo, mientras que los valores positivos se toman en la escala de grises hacia el blanco, cuanto más blanco más positivo (fig.6).
La proyección sobre el plano XY, conforma unas superficies de nivel, que determinarán la forma del orbital atómico 2p, con dos lóbulos bien diferenciados, debido a la aparición de un plano nodal, puesto que l=1, que será la característica de todos los OAp
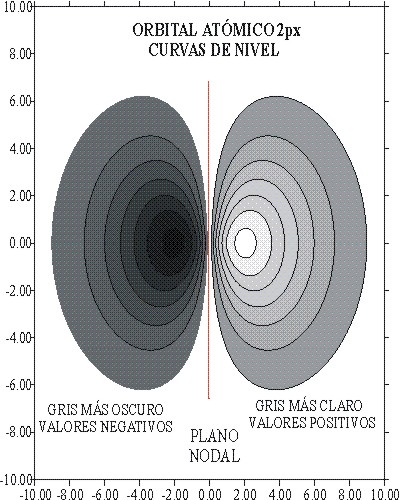
fig. 7
En
la figura 7, se observa el plano de dichas superficies y curvas de nivel
en las que R es constante. El máximo
ocurre a los 2 bohr, tal como se mostraba en la gráfica de la función
radial (fig. 1).
Estas funciones son las que se tomarán para formar los orbitales híbridos, o se superpondrán para formar los diferentes tipos de enlace covalente, siempre entre “lóbulos” del mismo signo.
Si se eleva la función R al cuadrado se obtiene la densidad de probabilidad que se representa en las figuras 8 y 9. Esta última se puede comparar con la gráfica de la función de onda 2px, que se da en la figura 7 y observar cómo se modifica el tamaño de la línea de contorno y las isolíneas correspondientes.
En este caso cada punto de la malla superficial indicará una densidad de probabilidad, que al proyectarse sobre el plano base (el XY para el OA 2px), producirá las curvas de nivel de probabilidad en las que R2 es constante.
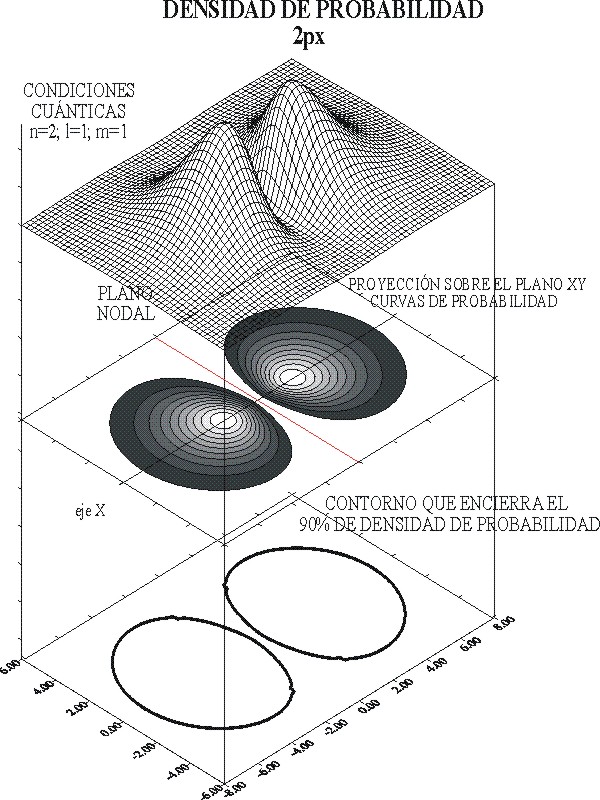
Fig.8
La línea de contorno en
el plano a que se haga referencia o superficie límite (si se tratara de
volúmenes), indicará la zona del espacio
que encierra una densidad de probabilidad acumulativa del 90% que
es lo que se dibuja habitual-mente
como orbital atómico.
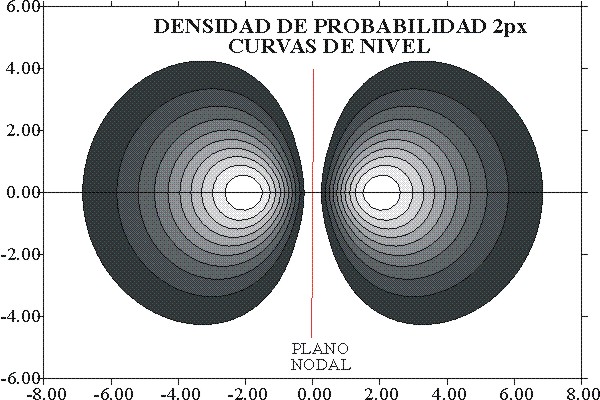
Fig.9
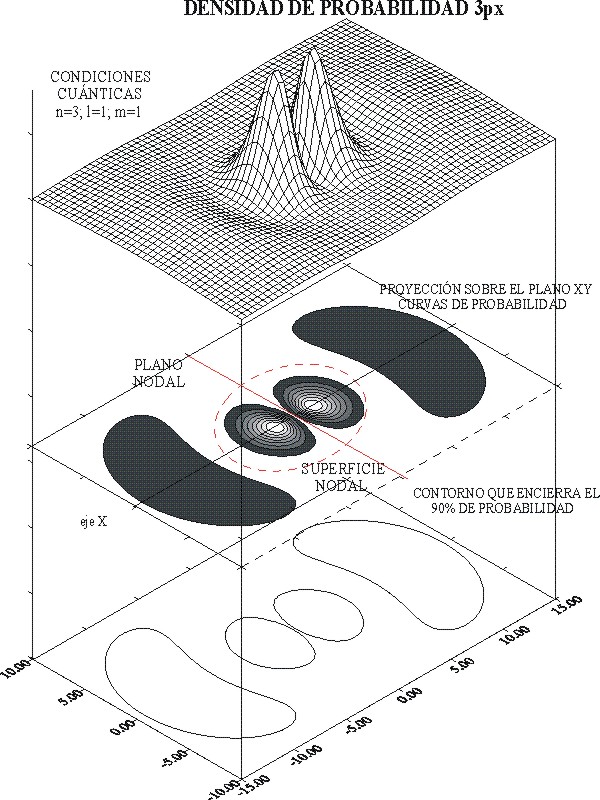
Fig. 10
La
figura 10, corresponde a la gráfica tridimensional de la densidad de probabilidad
para el OA 3px, y a
través de ella se puede comparar con la obtenida para el OA 2px.
Debe
observarse la forma real del orbital, en comparación con lo que normalmente
se lee en los textos. Como se ve, y pese a lo que se cree la forma del
OA 2px, no coincide exactamente con la del OA 3px
. Aparece una superficie nodal que
corresponde a los valores de R2=0
El
número de superficies nodales de un orbital atómico depende de los números cuánticos n y l , a través
de la expresión: n-(l+1), o sea 3-2=1
El mayor máximo (“montaña más alta), tiene lugar aproximadamente a 1,8 bohr. La superficie nodal a 6 bohr. La línea de contorno, llega casi a los 15 bohr ( para el 90%).
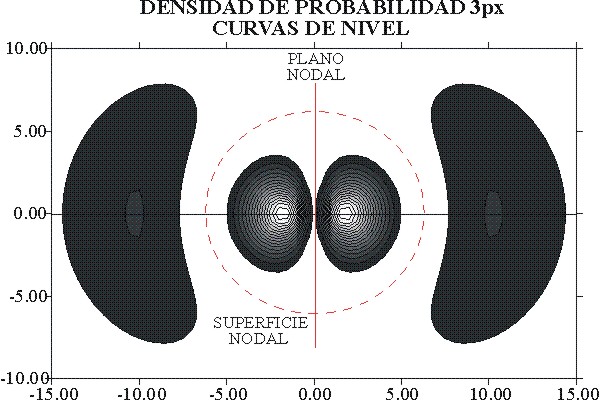
Fig. 11
En
la figura 11 se aprecia con detalle el mapa de las curvas de nivel de
densidad de probabilidad, que permite una mejor comparación con las que
corresponden al OA 2px. Siempre las distancias estarán referidas
a bohr.
Sin
embargo si se dibujara el OA como la línea que abarca 99% de densidad
de probabilidad acumula-tiva, debido a la pequeña pendiente que tiene
la superficie R2, la forma de la línea de contorno, y por lo tanto
de lo que se dibuja como orbital atómico en el plano, cambiaría bastante,
como se observa en la figura 12.
Si
se hiciera girar la línea de contorno externa dada sobre el eje X se produciría la representación espacial del
orbital atómico 3px.
En aquellos orbitales en los que aparezcan superficies nodales interiores, éstas quedarían prácticamente tapadas en la rotación, por eso la visión espacial no las contiene.
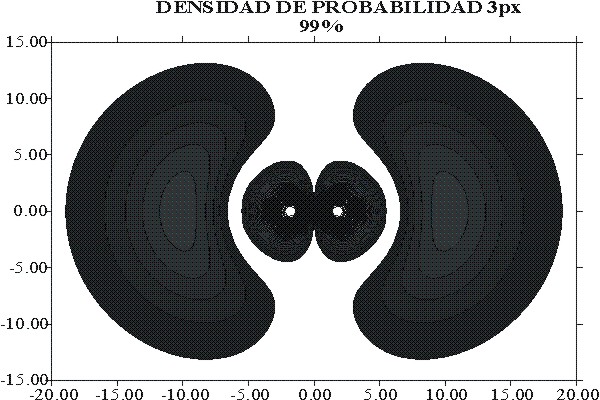
Fig. 12
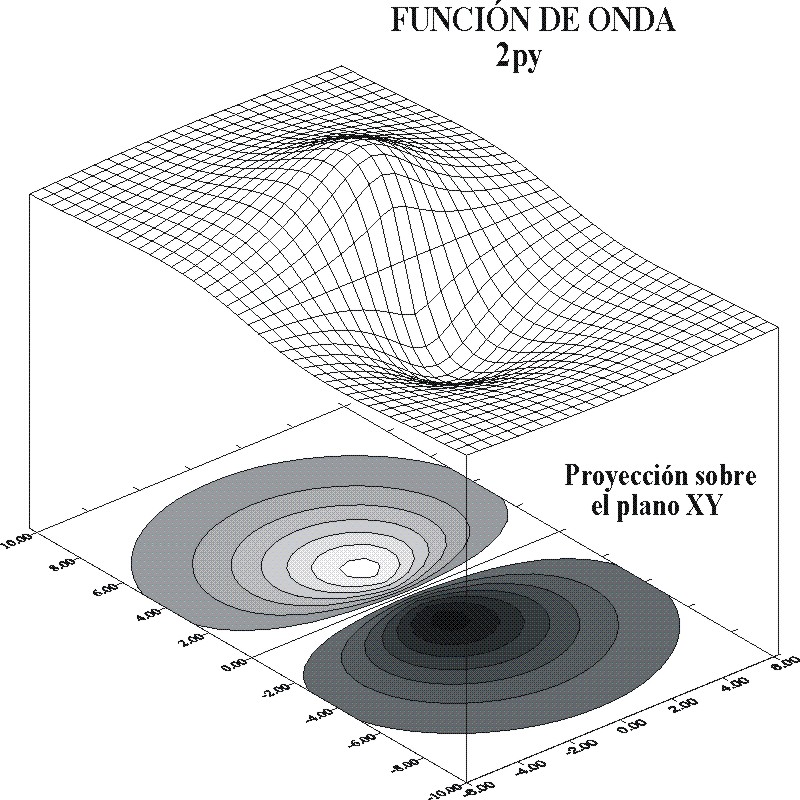
Fig. 13
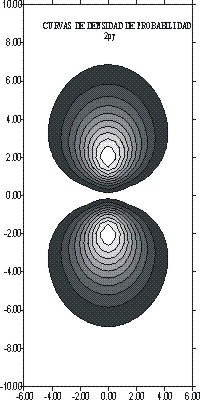
Fig.14