Fig.1
ENSEÑANZA DE LA FÍSICA Y LA QUÍMICA
INTRODUCCIÓN
A LOS CAMPOS ESCALARES Y VECTORIALES
1. QUÉ ES UN CAMPO.
Se denomina CAMPO en general, a toda magnitud
física cuyo valor depende del punto del plano o del espacio, y del instante
que se considere. Si la magnitud definida así en un punto del espacio es escalar,
el campo es escalar; si fuera vectorial,
sería un campo vectorial.
Ahora en invierno, si se tomara la temperatura
en diferentes puntos del aula de Física, se observaría que en cada instante,
la temperatura de ciertos puntos, los que se encuentran próximos a los radiadores,
sería diferente de la que tomamos junto a la puerta o ventanas. El aula se
convertiría así en un CAMPO ESCALAR DE LA TEMPERATURA.
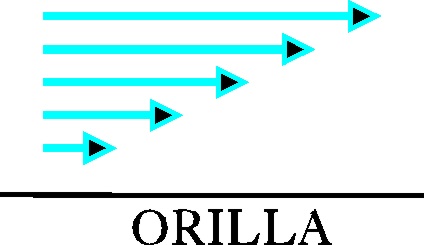
Si en un río echamos corchos a diferente
distancia de la orilla, observaríamos que la velocidad con que se moverían
debido a la corriente, sería distinta, mayor hacia el centro e inferior cerca
de la orilla. Estas velocidades variables con la distancia a la orilla, representarían
el CAMPO VECTORIAL DE LAS VELOCIDADES (fig.1).
Esta misma operación la podríamos realizar
en casa, llenando un lavabo de agua, disponiendo un corcho, cerca del borde,
y sacando el tapón. El régimen turbillonario del fluido al desaguar, produciría
una velocidad en el corcho que según la aproximación al desagüe sería mayor.
Si tomáramos las velocidades en distintas
líneas, observaríamos la distribución dada
(fig.2).
De forma más específica un CAMPO estaría
constituido por una distribución de magnitudes escalares, vectoriales definidas en función de las coordenadas espaciales
y del tiempo. Se debe recordar que una magnitud escalar requiere un único
número para su descripción completa, la vectorial 3
[1]
(las tres componentes, o el módulo, dirección y sentido).
2. CAMPOS ESCALARES.
Un ejemplo de campo escalar muy sencillo, es el de alturas
en un plano topográfico (fig.3). Cuando observamos esos planos, apreciamos
las curvas de nivel o lugares geométricos en los que la altura es la misma.
En el plano XY de la "isla misteriosa", a cada punto del plano dado,
le corresponde una determinada altura, dado que es una magnitud escalar, el
dibujo realizado corresponde al CAMPO ESCALAR DE LA FUNCIÓN ALTURA. Las curvas
de nivel, o lugares geométricos en los que la magnitud representada es la
misma, se denominan con carácter general LÍNEAS ISOTÍMICAS (En los campos
llamados CONSERVATIVOS, se denominarían LÍNEAS DE POTENCIAL).
La superficie encerrada por ellas sería una SUPERFICIE ISOTÍMICA (lugar geométrico en que H(x,y) = cte.).
Si la magnitud medida es la temperatura, serían ISOTERMAS,
en el caso de tratarse de la presión, serían ISOBARAS (las líneas que se aprecian en los mapas del tiempo que
aparecen en los informativos de televisión y que cuando están muy juntas anuncian
fuertes vientos). Otros campos escalares importantes, son los densidad de
población, y los de densidad electrónica.

Fig.1
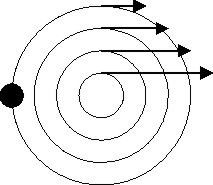
Fig.2
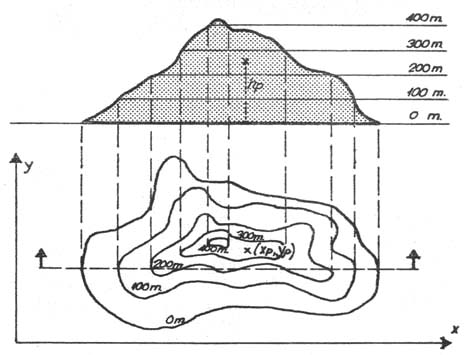
Fig.3
3. GRADIENTE.
Estamos acostumbrados a escuchar en la información
televisiva del tiempo, que cuando las isobaras están muy juntas, los vientos son fuertes, debido
a las alteraciones bruscas de presión. Igualmente sabemos que en un mapa topográfico,
cuando las curvas de nivel están próximas, el desnivel es mayor, y la zona
se supone abrupta. Pues bien, la magnitud que mide la máxima variación de
la función escalar considerada, con la variación de la posición, se denomina
GRADIENTE
[2]
, siendo su sentido hacia los valores crecientes de la magnitud
escalar que sufre la variación. En el caso de un campo escalar de alturas, el
gradiente nos indicaría la línea de máxima pendiente, dato muy importante
porque nos permitiría saber por donde discurriría el agua de un manantial
en una montaña, o por donde se debe efectuar el tendido de una línea eléctrica
si se pretende ahorrar material. Naturalmente, el agua en un manantial en
la montaña no discurre libremente hacia abajo, sino siguiendo
una dirección y sentido determinado, por eso el gradiente es una magnitud
vectorial que opera sobre otra escalar.
Así, utilizando coordenadas cartesianas, si tenemos una función escalar F(x,y,z) , siendo F (presión,
temperatura, altura, potencial, densidad electrónica etc.), el gradiente de
dicha función sería:
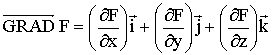 [3]
(1)
[3]
(1)
Por lo tanto, el gradiente representa
las derivadas parciales de una función escalar en un espacio vectorial, lo que
va a producir una derivada vectorial. Existe un operador vectorial o símbolo matemático que representa dicha operación,
consiste en el triángulo (delta) significativo del incremento
[4]
pero invertido, o sea con el vértice hacia abajo:
![]() [5]
. Por su forma, se le denominó NABLA (el nabla era un instrumento
musical de cuerda, tal como el arpa, empleado por sirios y persas), o ATLED
(delta al revés). Este operador fue creado por Hamilton a mediados del siglo
XIX.
[5]
. Por su forma, se le denominó NABLA (el nabla era un instrumento
musical de cuerda, tal como el arpa, empleado por sirios y persas), o ATLED
(delta al revés). Este operador fue creado por Hamilton a mediados del siglo
XIX.
De esta forma, el NABLA como operador matemático en coordenadas cartesianas
es:
![]() (2)
(2)
Por este motivo
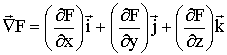 es un vector:
es un vector:
cuyo módulo es
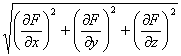 y (3)
y (3)
Su dirección será tal que suponga
la máxima variación de la función.
Como sentido de dicha variación siempre se tomará el creciente
APLICACIÓN
Ej1. Cálculo de un gradiente.
Dada la función escalar V = 2x2 + 3y2
+ z2. Determine el gradiente en el punto P (1,1,1):
![]()
Se deriva la función respecto
a x , y , z y después se sustituyen los valores dados:
![]()
Ej2 Calcule el gradiente del campo escalar U = sen(xy/2) .
Observación: Al derivar la función respecto a x, todo lo que no sea x se considera constante, y así
en las sucesivas derivaciones (respecto a y).
SOLUCIÓN:
![]() U = (y/2)cos (xy/2)
U = (y/2)cos (xy/2)
![]() + (x/2)cos(xy/2)
+ (x/2)cos(xy/2)
![]()
En un campo de alturas como el que se presenta
(fig.1, mapa topográfico en unos ejes x/y), el gradiente:
![]() (4)
(4)
permitiría conocer en cada punto del terreno,
la máxima variación de la altura con la distancia. Siendo
![]() un vector unitario en la dirección radial.
un vector unitario en la dirección radial.
Multiplicando escalarmente por
![]() los dos miembros.
los dos miembros.
![]()
(Producto escalar
[6]
del gradiente por su desplazamiento).
Si H=cte. dH=0
Por lo tanto el gradiente de una función
a lo largo de una curva de nivel o línea isotímica (circunferencias en la
fig.4, H= cte.), deberá ser perpendicular a dicho desplazamiento ya que dH=0
, al ser el diferencial de una constante y puesto que se trata de un producto escalar (coseno
del ángulo formado por curva de nivel y el gradiente =0 , por lo que dicho
ángulo = 90º ).
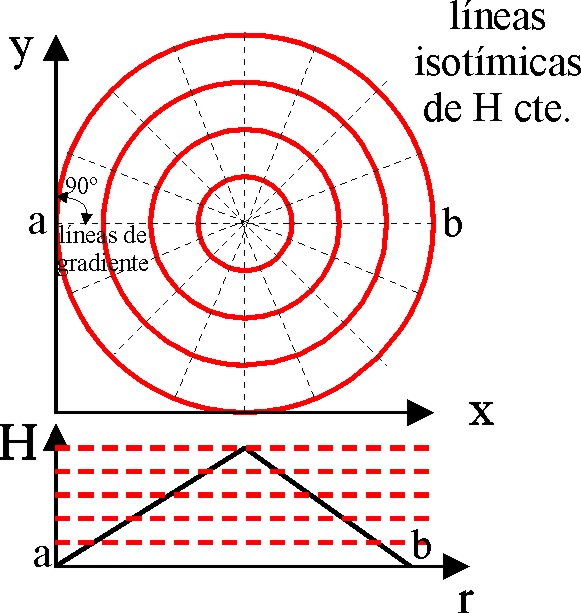
Fig.4
Una propiedad del gradiente, es ser perpendicular
a cualquier superficie isotímica en
todos sus puntos y con sentido hacia los valores crecientes de las superficies
isotímicas.
¿Qué
importancia tiene esta propiedad?.
Si
se quiere calcular el vector unitario perpendicular a una superficie en un
punto de la misma, bastaría con calcular
el gradiente, y después aplicar el concepto de vector unitario (llamado a
veces versor).
APLICACIÓN
Ej3. Dada la superficie S= x2 + (y-2)2 + (z+1)2 = 0, calcule
un vector unitario normal a dicha superficie por el punto (2,0,-2).
PASOS A SEGUIR:
a) Determinación del
![]() , derivando la función superficie respecto
a x, y, y z.
, derivando la función superficie respecto
a x, y, y z.
![]()
b) Se calcula su valor numérico, sustituyendo las coordenadas
del punto:
![]()
c) Se determina el módulo del gradiente, aplicando la fórmula
(3) : 6
d) Se divide el vector, por el módulo de dicho vector :
![]()
![]()
¿Cuál
sería la unidad del gradiente?
Sería
la de la magnitud escalar medida / unidad de longitud.
Si en cada punto del campo escalar, calculáramos el gradiente, e incluso pudiéramos dibujarlo, tendríamos un CAMPO DE GRADIENTES, que sería naturalmente un CAMPO VECTORIAL. La propiedad del gradiente citada anteriormente, permite trazar en un campo escalar una serie de líneas perpendiculares (ortogonales) a las superficies de nivel, tales que los vectores gradiente sean tangentes a dichas líneas. En este caso, dichas líneas serían las LÍNEAS DEL CAMPO DE GRADIENTES.
En el campo escalar de alturas H(x,y) de
la figura 5 se puede apreciar, al proyectar los gradientes sobre el plano
XY, el aspecto de un campo de gradientes, en el cual
![]() . Los vectores tendrían
un sentido hacia la cúspide (sentido creciente), siguiendo la dirección
de la máxima variación. Este hecho podría servir para resolver los siguientes
problemas:
. Los vectores tendrían
un sentido hacia la cúspide (sentido creciente), siguiendo la dirección
de la máxima variación. Este hecho podría servir para resolver los siguientes
problemas:
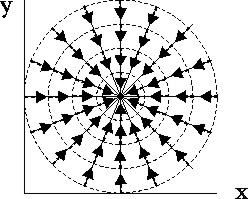
Fig.5
APLICACIÓN
Ej4. Calcular la dirección y el sentido según el cual, se produce la máxima variación de la función F=2xz-y2, en el punto (1,2,3). ¿Cuál es el módulo de este máximo valor?
PASOS A SEGUIR:
a) Se calcula el gradiente en
dicho punto.
![]()
b) Se determina el módulo del vector gradiente =
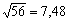
En un campo escalar de temperaturas, si
se establecen las curvas de nivel térmico (ISOTERMAS), entre los focos caliente y frío, y se dibujan los gradientes
perpendiculares en cada punto a la curva. El campo de gradientes estaría constituido
por todo el espacio donde se establecen los diferentes gradientes. Esto se
podría elaborar en invierno en el aula de física (fig.6), con un termómetro
sensible, dejando alguna ventana abierta (foco a menor temperatura),
trazando las isotermas que se acercan al foco caliente (radiador),
y en la que cada alumno podría ser el punto de aplicación del vector gradiente,
estableciendo el campo de gradientes.
En un aula de 8 por
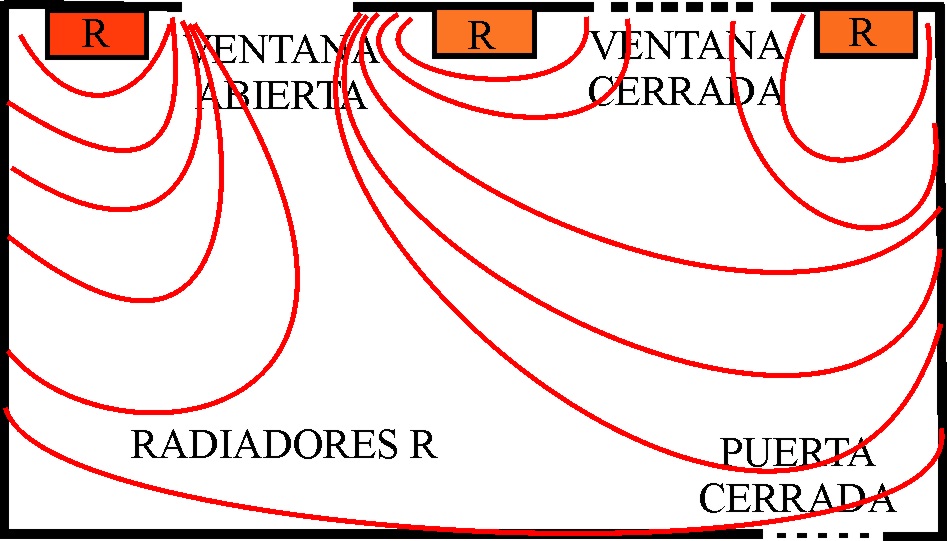
Fig.6
Cuando se dan campos escalares que son conservativos,
la función escalar que los engendró se deno-mina FUNCIÓN POTENCIAL V, y ![]() del campo de gradientes es EL GRADIENTE DE DICHA FUNCIÓN:
del campo de gradientes es EL GRADIENTE DE DICHA FUNCIÓN:
![]() . (5)
. (5)
De esta forma dada la función potencial
de un campo, se podría determinar la intensidad del campo de gradientes. Así
mismo si V es constante,
![]() = 0
= 0
¿Por qué el signo menos?
El
signo menos surge en virtud de la igualdad vectorial, dado que el gradiente
por convenio tiene siempre sentido creciente, mientras que la intensidad de
un campo lo tiene al contrario.
APLICACIÓN
Ej5. Dada la función potencial U = x3+ y3 + z3, calcular la intensidad de su campo de gradientes en el punto (1, 1, 1) Siguiendo la mecánica aplicada en los ejercicios anteriores:
a)
![]()
5. CAMPOS VECTORIALES.
Los campos más estudiados son los vectoriales
[7]
, puesto que vivimos inmersos en ellos, interaccionado a
través de dichos campos toda la materia. Los campos que marcan las interacciones
que ocurren en la naturaleza, son CAMPOS DE FUERZAS
[8]
, entre los que tenemos: EL CAMPO GRAVITATORIO, creado por
la interacción entre masas, EL CAMPO ELECTROMAGNETICO, originado por la interacción
entre cargas (eléctrico si las cargas están en reposo, y magnético si están
en movimiento). En estos campos las fuerzas surgen sin soporte material, y
tienen un alcance infinito. Existen otros campos de fuerzas en los que es
necesario dicho soporte, y son de corto alcance: EL CAMPO NUCLEAR, responsable
de la interacción nuclear, y el CAMPO DÉBIL, que regula la interacción entre
diferentes tipos de partículas nucleares.
¿Cuál
es el origen
[9]
de los campos de fuerzas?
Antiguamente se justificaban a través de
la acción de la magnitud creadora del campo, llamada FUENTE DE CAMPO o MAGNITUD ACTIVA A, a través del espacio. Así
para explicar por qué una masa (
Sin embargo si en otro punto de la tela se sitúa una bola
de acero, ésta sí la deformará, y la bola de cristal se acercará a ella. Por
lo tanto, la bola de acero actuará como fuente
de un campo que perturbando el medio en que se encuentra y deformando su espacio,
es capaz de actuar sobre la otra bola (fig.7).
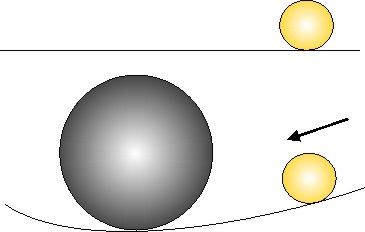
Fig.7
| CAMPO |
MAGNITUD ACTIVA A |
INTENSIDAD
|
UNIDADES |
INTERACCIÓN
|
k (u.S.I.) |
TIPO (magnitudes semejantes) |
| Gravitatorio |
Masa m
|
|
N/kg o m/s2 |
|
6,67.10-11 |
ATRACTIVA |
| Eléctrico |
Carga, q |
|
N/C o V/m |
|
9.109
|
REPULSIVA O Atractiva |
| Magnético |
Carga en movimiento, q
|
|
N.s/C.m (Tesla, T) |
|
10-7 |
REPULSIVA O Atractiva |
a) En el campo eléctrico
![]() (siendo
(siendo
![]() el coeficiente dieléctrico o permitividad
del medio), mientras que en el campo magnético es
el coeficiente dieléctrico o permitividad
del medio), mientras que en el campo magnético es
![]() , siendo : la permeabilidad magnética del medio.
, siendo : la permeabilidad magnética del medio.
b) En el campo gravitatorio y eléctrico, la intensidad
del campo tiene la misma dirección
que la fuerza, dado que la magnitud activa es escalar, sin embargo
no ocurre lo mismo en el magnético, pues la velocidad
![]() es un vector y la fuerza sobre una carga en un campo
es un vector y la fuerza sobre una carga en un campo
![]() responde a un producto vectorial
responde a un producto vectorial
![]() [13]
[13]
c) Si los campos vectoriales estuvieran integrados
por varias magnitudes activas, sus efectos o intensidades se sumarían vectorialmente,
a partir de un principio llamado de superposición de cam-pos, de tal modo que
la presencia de cada uno no perturba la acción de los demás de modo individual.
6. LÍNEAS
DE FUERZA
En 1838, Faraday, a través de los experimentos
realizados con los campos magnéticos y visualizar como se orientaba el polvillo
de hierro en tales campos, sugirió una forma de visualizar los campos de fuerzas,
surgiendo lo que denominó LÍNEA DE FUERZA (“línea de fuerza móvil”)
[14]
. Las líneas de fuerza de un campo vectorial, deben cumplir
estas condiciones:
a) En cualquier punto del campo, su intensidad deberá
ser tangente a dicha línea, lo que
matemáticamente se puede expresar de forma que el producto vectorial de la
intensidad del campo por un desplazamiento infinitesimal a lo largo de la
línea del campo será nulo.
![]() (como el producto vectorial depende del seno
del ángulo formado, si es 0, por ser tangente,
sen
(como el producto vectorial depende del seno
del ángulo formado, si es 0, por ser tangente,
sen
![]() =0)
=0)
b) En los campos eléctricos y gravitatorios, la
línea de fuerza corresponderá aproximadamente a la trayectoria que seguiría
la unidad de magnitud activa abandonada en dicho campo, si se moviera a velocidad
constante
[15]
o si su magnitud activa fuera despreciable. El
vector campo existente en ese punto es siempre tangente a la línea de fuerza.
c) A efectos de visualizar el campo se dibujan las líneas de
fuerza
[16]
de un determinado campo más o menos apretadas. Allí donde
sea más intenso van más juntas mientras que donde es menos intenso van más
separadas. Por lo tanto no es arbitrario sino que está relacionado con la
intensidad de dicho campo, de tal forma que el
número de líneas de fuerza que atraviesa perpendicularmente un elemento
de superficie, deberá ser proporcional a su intensidad. Este conjunto de
líneas de fuerza se denomina flujo
![]() , de tal forma que:
, de tal forma que:
![]() (6) (
(6) (
![]() producto escalar).
[17]
producto escalar).
[17]
Así, por ejemplo para visualizar el campo
creado por la carga eléctrica positiva, de
una carga de 10C deberán salir 10 veces más líneas de fuerza que de otra de
1 culombio.
6.1.
LÍNEAS DE FUERZA Y DE POTENCIAL EN EL CAMPO GRAVITATORIO
En los campos gravitatorios creados por
masas aisladas, dado que dichos campos son atractivos, las líneas de fuerza
deberán ser entrantes, en la magnitud activa, coincidiendo su dirección con
la de los radios (fig.8). Si se abandona por lo tanto una unidad de
masa m en uno de los puntos dados, A, B, o C, seguiría aproximadamente la
trayectoria indicada por la línea de fuerza hasta terminar en M (ver nota
final 12).
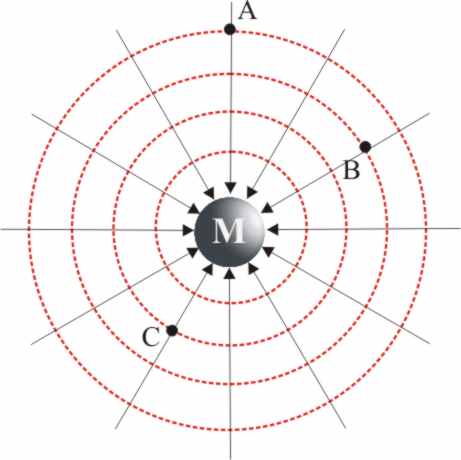
Fig.8
Si el campo se originara por la acción de
varias masas, éstas se curvarían, de forma que en cada punto la intensidad
del campo resultante fuera TANGENTE a
la línea de fuerza.
En la fig.9, los campos gravitatorios creados
por cada masa M, en el punto P,
![]()
![]() y
y
![]() , que individualmente son radiales y dirigidos a las masas respectivas se
suman vectorialmente, y la intensidad resultante
, que individualmente son radiales y dirigidos a las masas respectivas se
suman vectorialmente, y la intensidad resultante
![]() , es tangente a la línea de fuerza que pasa por P.
, es tangente a la línea de fuerza que pasa por P.
Las líneas isotímicas de potencial (curvas
rojas punteadas), se cortan perpendicularmente con las líneas de fuerza en
cada punto del campo.
6.2.
LÍNEAS DE FUERZA Y DE POTENCIAL EN EL CAMPO ELÉCTRICO.
En los campos eléctricos podremos considerar
dos casos, según sean creados por la carga positiva que se toma como patrón
desde los experimentos de Benjamín Franklin a mediados del siglo XVIII ("los
cuerpos adquirían electricidad cuando se cargaban positivamente"), o
por la carga negativa
[18]
. En el primer caso las líneas de fuerza son salientes,
y la magnitud activa actúa como una FUENTE DE LÍNEAS DE FUERZA, coincidiendo
con los radios cuando se trata de cargas aisladas (fig.10).
Si la magnitud activa fuera la carga negativa,
el campo eléctrico actuaría como el
gravitatorio (fig.11).
Si el campo se origina por superposición
de efectos de varias cargas de igual o diferente signo, las líneas de fuerza
se curvarán de forman que salgan de las
positivas y entren las negativas. Obsérvese
la figura 12 con líneas de fuerza saliendo de la carga + y entrando en la
-. La intensidad del campo debido a cada carga Q, E1 y E2,
son radiales, respecto a las mismas. La intensidad resultante ET, la suma vectorial de ambas,
será tangente a la línea de fuerza en ese punto(fig.12 y 13).
En cualquier caso por un mismo punto del espacio SÓLO
PODRÁ PASAR UNA ÚNICA LÍNEA DE FUERZA, dado que el principio de superposición
de los campos individuales impediría lo contrario; sólo el campo resultante
de la acción de varias magnitudes activas, será el tangente a la línea de
fuerza que será ÚNICA.
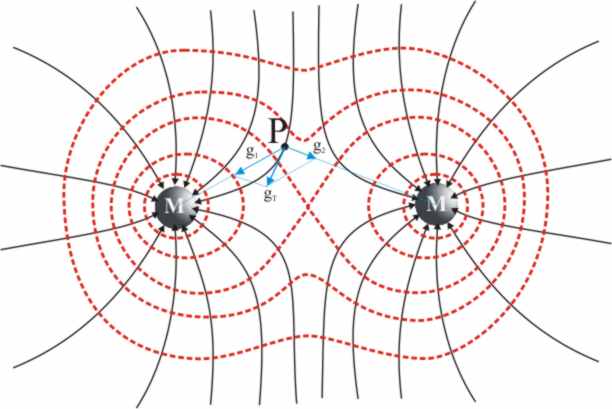
Fig.9
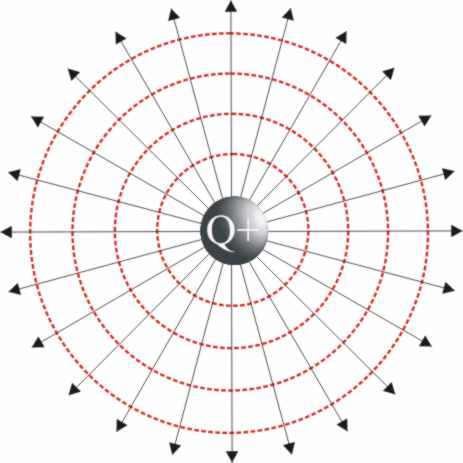 Fig.10
Fig.10
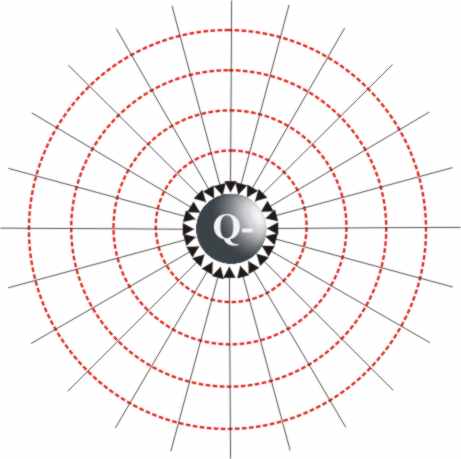 Fig.11
Fig.11
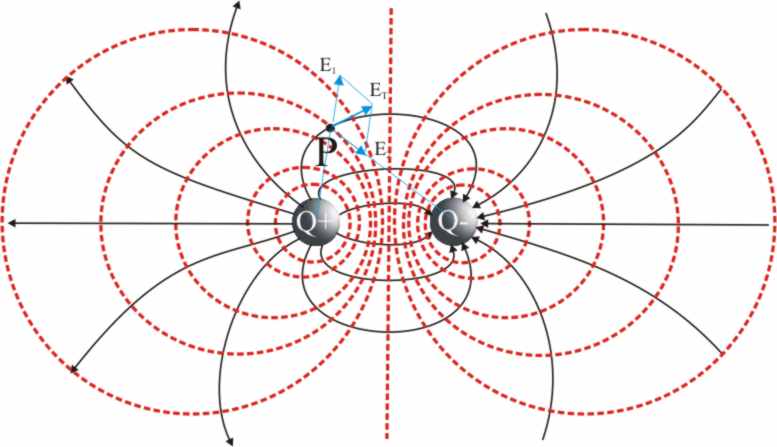 Fig.12
Fig.12
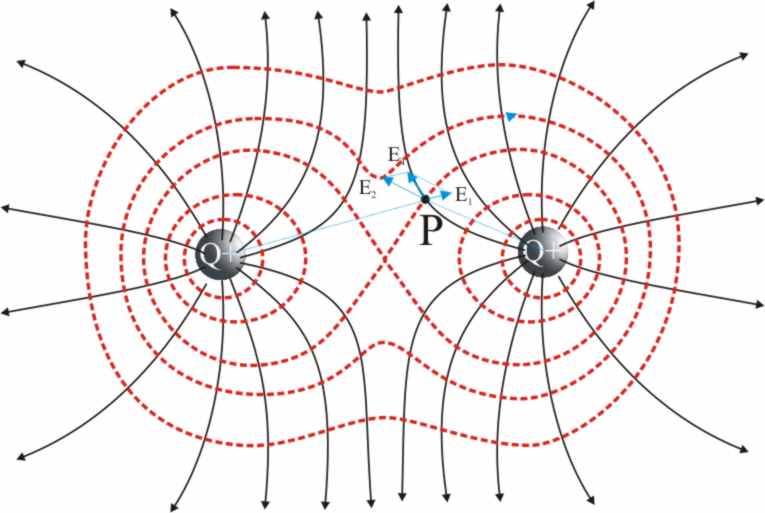
Fig.13
6.3.
LÍNEAS DE FUERZA DEL CAMPO MAGNÉTICO.
En los campos magnéticos creados por cargas
en movimiento que circulan por un conductor (corrientes eléctricas), las líneas
de fuerza son circunferencias concéntricas cuyos centros serán los diferentes
puntos del conductor por donde circulan (fig.14), debido a que se cumplirá
el producto vectorial, los vectores campo magnético siempre serán tangentes
a ella, y estarán en planos perpendiculares a dicho conductor, que deberá
contener en cada instante a la carga en movimiento.
Si el elemento por donde circula la carga
realice un movimiento circular o sucesivos movimientos circulares (un imán,
o un solenoide, conductor en espiral de radio constante) (fig.15, 16, y 17),
las líneas de fuerza ya no serán circunferencias concéntricas, como se aprecia
en los dibujos. Pero son siempre líneas
cerradas, a diferencia de las líneas de fuerza de los campos eléctricos y
gravitatorios que son abiertas.
Si se difunde polvo de hierro, en el plano
perpendicular a un conductor, la distribución de la granalla de hierro, marcará
la trayectoria de las líneas de fuerza del campo magnético, para el caso de
un conductor rectilíneo (fig.18), una espira circular (fig.19), un solenoide
(fig.20) y un imán recto (fig 21).
Conviene diferenciar las líneas cerradas
que pasan a través de un imán o de un solenoide (conductor en espiral de radio
constante), con las abiertas de un dipolo, que salen de la carga positiva
y entran o mueren en la negativa. Se puede apreciar a través de los dibujos,
la similitud entre las líneas de fuerza del campo magnético creado por un
imán recto (fig.17 a y b), y las originadas por la corriente que circula por
un solenoide. En la figura 17b superior, en el convenio del dibujo, un círculo
con un punto indica que la corriente que circula por el conductor (de sección
circular)se aproxima al lector que ve el dibujo, mientras que la cruz, expresa
que se aleja. Este convenio se sigue en las espiras del solenoide de la figura
17 a superior.
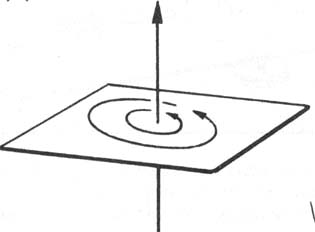
Fig.14
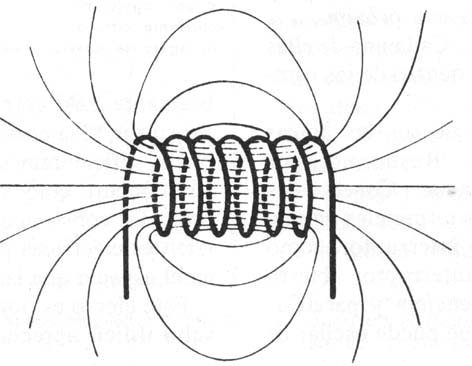
Fig.15
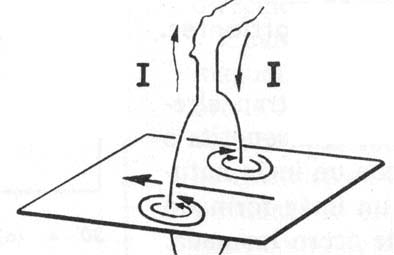
Fig.16
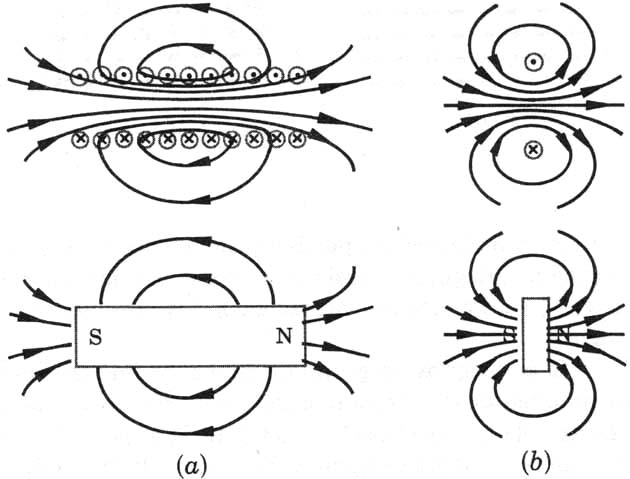
Fig.17

Fig.18

Fig.19

Fig.20

Fig.21
[1]
Los términos escalar y vectorial, surgen
por primera vez en el trabajo del matemático irlandés Hamilton sobre quaterniones
(números complejos multidimensionales), de 1844. El escalar procede de la
escala de progresión de los números desde negativo hasta infinito. A la
parte imaginaria de los quaterniones, que se construía con un radio y el
ángulo, lo denominó, parte vectorial, o simplemente vector.
[2]
El término gradiente, significa tal como
grado, escalón, o escala, aunque originalmente, procede del latín gradiens-entis "el que anda", refiriéndose al camino
por una pendiente.
[3]
Los vectores unitarios i, j y k, fueron introducidos por Hamilton. Al mismo tiempo se emplearon las letras
",$ y ( para representar-los. Por lo general
los vectores se simbolizaron por letras griegas (Tait, Hamilton y Gibbs),
e incluso por letras góticas (Maxwell y Heaviside. Tait y Gibbs, comenzaron
a incluir un segmento encima de las letras que lo simbolizaron. El uso del
símbolo de vector encima del representado es un convenio actual y personal que pretende reforzar dicho carácter, pero que
no aparece en el libro verde de la IUPAP (el libro verde engloba todos los
convenios, en unidades y símbolos
de la unión internacional de física pura y aplicada, como primera opción.
En éste los vectores se simbolizan en negrita de tal forma que r=xi+yj+zk.
Sólo como segunda opción y en sentido del reforzamiento se emplearía dicho
símbolo, que se podría confundir con el que indica la tendencia.
[4]
Realmente no es el triángulo el representativo del incremento, sino la
letra griega delta, que indica un
elemento diferencial, o sea una diferencia infinitesimal, pues corresponde
a la d (diferencia) en griego (delta).
[5]
En el trabajo de Hamilton de 1846,
esta operación se representó por primera vez por un simple triángulo con
un vértice dirigido hacia la izquierda (no hacia abajo),
![]() , y no recibía el nombre de nabla (ya que no se parecería a un arpa), nombre
que fue propuesto por Robertson Smith, al físico matemático escocés Tait que lo publicó
en sus libros, y se generalizó a partir de 1870. También en 1852, el inglés
O’Brien, representó una operación similar en el contexto de la traslación
de vectores, que representó por S, de tal forma que siendo los vectores unitarios, ",$ y (,
, y no recibía el nombre de nabla (ya que no se parecería a un arpa), nombre
que fue propuesto por Robertson Smith, al físico matemático escocés Tait que lo publicó
en sus libros, y se generalizó a partir de 1870. También en 1852, el inglés
O’Brien, representó una operación similar en el contexto de la traslación
de vectores, que representó por S, de tal forma que siendo los vectores unitarios, ",$ y (,
![]()
![]() .El uso del vector encima del símbolo nabla es prescindible (no aparece
en el libro verde de la IUPAP); sólo se emplea para reforzar el carácter
vectorial.
.El uso del vector encima del símbolo nabla es prescindible (no aparece
en el libro verde de la IUPAP); sólo se emplea para reforzar el carácter
vectorial.
[6]
Las operaciones producto escalar y producto
vectorial, no se llamaron así inicialmente sino producto directo y
producto sesgado. Después una vez denominados tal como en la actualidad,
se representaron con la inicial S (escalar) y la V(vectorial), sin ningún
símbolo y delante de los vectores dados (así aparecen en todos los trabajos
de Maxwell). Tait, en su tratado sobre cuaterniones de 1867, definió el
producto escalar de los vectores " y $, que forman un ángulo 1 como S"$=-T"T$ cos1
mientras que el vectorial V"$=T"T$sen1.0,
siendo T el módulo de cada vector y 0,
un vector unitario perpendicular a " y $. Fue el ingeniero norteamericano Gibbs,
el que introdujo en su libro de “Elementos de análisis vectorial” de 1881,
el . y la x , para representarlos.
[7]
Einstein en su libro:”La evolución de la
Física” de 1961, escribe que:”El concepto de campo es el invento físico
mas importante desde los tiempos de Newton”.
[8]
La acción a distancia ya fue postulada por Newton, pero la teoría de los campos
vectoriales se puede atribuir a Faraday, entre 1830-60. Después de estudiar
los experimentos de Oersted y de Ampère, y apoyándose en las ideas metafísicas
de Boscovich y Kant, supone que dichas acciones implican campos de puntos
de fuerza, cuya sucesión forman las “líneas
de fuerza móviles”, unificando las acciones gravitatorias, eléctricas
y magnéticas, aunque no fuera partidario de la acción a distancia, sino
a través de los puntos de fuerza, ya que según él las líneas de fuerza curvadas,
características del campo magnético se oponían a la acción a distancia,
que presuponía líneas rectas.
[9]
La
teoría de los campos de fuerza evolucionó mucho desde Faraday, Thomson,
Maxwell, Heaviside, Lorentz hasta Einstein. Para Faraday, el campo estaba
lleno de líneas de fuerza, cuya distribución dependía de la de los cuerpos
situados en su seno, de forma que la acción mecánica y eléctrica sobre cada
cuerpo venía determinada por las líneas que convergían en él. Maxwell, rechaza
la teoría de los campos de fuerza de Faraday aplicada a los cuerpos, adoptando
una teoría de la carga y de la corriente fundamentada en el concepto de
campo. Explicaba los campos eléctricos y magnéticos como materia en movimiento.
Estos campos eran independientes
aunque se impenetraban. Según Maxwell, la materia ordinaria se cargaba al
desplazar el material de las bolas eléctricas que contiene
en su interior (debe recordarse que el electrón se descubriría casi 50 años
después). Estas bolas eléctricas inmateriales arrastraban unos remolinos
materiales magnéticos en forma de tubos hexagonales, como si fuera un engranaje,
siendo las aristas de los hexágonos las correas de transmisión. Cuando las
bolas eléctricas saltaban de un remolino a otro, producían calor. En su
“Treatise on Electricity and Magnetism”,
de 1865, decía lo siguiente: “La fuerza
magnética es el efecto de la fuerza centrífuga de los remolinos. La inducción
magnética es el efecto de las fuerzas cuando varía la velocidad de los remolinos”.Lorentz,
adaptó la teoría de campos, a los electrones que ya se habían descubierto,
y Einstein, introduce el espacio curvo y la relación masa energía en
la teoría de campos.
[10]
La palabra GRAVEDAD, se empleó en castellano,
mucho antes del descubrimiento de
[11]
Inicialmente se creía que el medio donde
se producía la interacción era lo que se denominaba éter, transmitido de la filosofía griega
[12]
Un cuadro mas completo de relaciones vectoriales se presenta en esta web,
en la sección”Cuadros de conceptos relacionables”. Título: Campos vectoriales.
[13]
Maxwell, a la intensidad del campo magnético,
la representó por la letra H, y medía la velocidad de los remolinos magnéticos
en su superficie, de forma que la dirección de H se tomaba a lo largo del
eje del remolino.
[14]
En 1845, William Thomson, mas tarde Lord Kelvin, proporcionaría a Faraday
el tratamiento matemático de las líneas de fuerza. Faraday atribuía a las
líneas de fuerza un movimiento continuo en el espacio y en el tiempo, estableciendo
el principio de conservación de la fuerza y llegando a explicar la radiación
y la luz, como un estado de vibración de las líneas de fuerza. El desarrollo
de la teoría de las líneas de fuerza fue completado por Maxwell, a través
de sus trabajos de 1855 (“On Faraday’s
Lines of Force”) y 1861 (“On Physical
Lines of Force”), aunque a diferencia de las de Faraday, éstas tenían
masa, siendo como “barras flexibles
con superficies rugosas” dependientes de la permeabilidad del medio
m. Einstein, no era partidario de las líneas de fuerza.
[15]
Lo que
ocurre es que al acelerarse la magnitud activa por efecto de la fuerza,
se sale de dicha trayectoria. Sólo cuando dicha fuerza es despreciable y
la aceleración tiende a cero, la sigue.
[16]
En 1845, William Thomson, mas tarde Lord
Kelvin, proporcionaría a Faraday el tratamiento matemático de las líneas
de fuerza. Faraday atribuía a las líneas de fuerza un movimiento continuo
en el espacio y en el tiempo, estableciendo el principio de conservación
de la fuerza y llegando a explicar la radiación y la luz, como un estado
de vibración de las líneas de fuerza. El desarrollo de la teoría de las
líneas de fuerza fue completado por Maxwell, a través de sus trabajos de
1855 (“On Faraday’s Lines of Force”) y 1861 (“On Physical Lines of Force”), aunque a diferencia de las de Faraday,
éstas tenían masa, siendo como “barras
flexibles con superficies rugosas” dependientes de la permeabilidad
del medio m. Einstein, no era partidario de las líneas de fuerza.
[17]
Una definición mas general del flujo, fuera del nivel
de esta introducción a los campos vectoriales sería, “la integral de superficie
de la componente normal del vector a que hace referencia el campo”
[18]
Benjamín Franklin creía que durante la descarga eléctrica solamente
circulaba un fluido cuyas partículas se repelían entre sí y atraían a las
de la materia ordinaria. La ley de la interacción eléctrica entre cargas
(inversa del cuadrado de la distancia, fue explicada por el químico Priestley,
antes que por Coulomb, que realizó
la parte experimental, mientras que la de la interacción magnética, también
inversa a dicho cuadrado, fue enunciada por Maxwell, que a través de 8 ecuaciones
en su “A Dynamical Theory of the
Electromagnetic Field”, de 1864, dio el aporte matemático para explicar
el comportamiento del campo electromagnético(al aplicarlas sobre los distintos
ejes, algunas aparecían triplicadas). Estas ecuaciones fueron convertidas
en 6 por Heaviside, que las desarrolló matemáticamente, y en 4, por Lorentz.
Actualmente son: la divergencia del campo eléctrico es proporcional a la
densidad de carga eléctrica:
![]() ; el rotacional de la
intensidad del campo eléctrico es igual a - la variación de la intensidad
del campo magnético con el tiempo,
; el rotacional de la
intensidad del campo eléctrico es igual a - la variación de la intensidad
del campo magnético con el tiempo,
![]() . La divergencia de la intensidad del campo magnético es nula
. La divergencia de la intensidad del campo magnético es nula
![]() , por fin relaciona el rotacional
de la intensidad del campo magnético con la variación del campo eléctrico
con el tiempo, y con la densidad de la carga en movimiento:
, por fin relaciona el rotacional
de la intensidad del campo magnético con la variación del campo eléctrico
con el tiempo, y con la densidad de la carga en movimiento:
![]() . Si no se depende del tiempo, la
segunda ecuación es nula, así como el término
. Si no se depende del tiempo, la
segunda ecuación es nula, así como el término
![]() .
.